Cadence / DSD 1 / БТ / 8-9

23

8. Нелинейные модели БТ в SPICE

8.1. Модель Гуммеля-Пуна

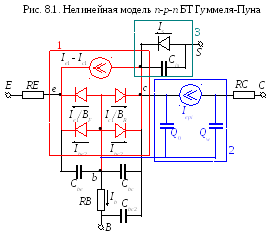
На рис. 8.1 представлена нелинейная эквивалентная схема БТ типа п-р-п (структура на рис. 1.1), которая используется в полной модели Гуммеля-Пуна.

8.1.1. Статический режим внутреннего транзистора.

Пунктиром 1 обведены элементы, описывающие статические ВАХ внутреннего транзистора. Эта часть эквивалентной схемы соответствует рис. 4.2б со следующими уточнениями:

1). Ток I_be2 через эмиттерный переход включает все его составляющие, показанные на рис. 2.1 (распределение токов в БТ), а именно:

• дырочную составляющую I_eр,

• ток рекомбинации-генерации носителей заряда в переходе I_erg.

2). Ток I_bс2 через коллекторный переход включает все его составляющие, показанные на рис. 2.1 ), а именно:

• дырочную составляющую I_ср,

• ток рекомбинации-генерации носителей заряда в переходе I_сrg,

• ток инжекции электронов из коллектора в пассивную базу I_c2.

3). Все составляющие токов I_be2 и I_bс2 включают токи через периферийные (торцевые) участки р-п переходов (рис. 1.1).

Таким образом,

;

.

В модели ВАХ диодов имеют следующий вид:

; (8.1а)

, (8.1б)

где и — масштабные (тепловые) токи, и — коэффициенты неидеальности.

Для токов I_eр и I_ср теоретические значения — коэффициентов неидеальности равны 1, для токов I_erg и I_сrg — 2, для тока I_c2 — между 1 (НУИ) и 2 (ВУИ). По умолчанию = = 1,5.

Возможно описание каждой составляющей тока отдельным уравнением с собственными значениями параметров и .

Токи I_e1 и I_с1, описывающие транзисторный эффект, определяются уравнениями (3.6) – (3.7). В модели в эти уравнения также введены корректировочные коэффициенты неидеальности и , теоретические значения которых (принятые по умолчанию) равны 1:

, (3.6а) , (3.6б)

, .

8.1.2. Область активного п- коллектора.

Пунктиром 2 обведены элементы, описывающие область активного п-колектора. Элементы этой части эквивалентной схемы описываются уравнениями (6.1) и (6.2а,б) раздела 6.

8.1.3. Изолирующий переход (коллектор-подложка).

Пунктиром 2 обведены элементы, описывающие изолирующий переход коллектор-подложка. Статический ток через этот переход имеет стандартную ВАХ:

,

где — напряжение на переходе коллектор-подложка.

8.1.4. Динамические элементы (емкости).

Каждая из емкостей р-п переходов является суммой барьерной и диффузионной емкостей.

Для барьерных емкостей используются унифицированные ВФХ, аналогичные ВФХ емкостей сток-подложка и исток-подложка в МДП-транзисторе (см. раздел 12).

Так, например, ВФХ барьерной емкости эмиттерного перехода имеет вид:

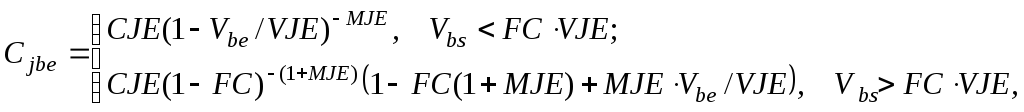
где при , — контактная разность потенциалов.

Емкость перехода база-коллектор расщеплена на две составляющие, одна из которых () соответствует активной части перехода, а другая () — пассивной. Эта мера необходимо вследствие того, что из-за конечного сопротивления базы внетрений (в) и внешний (В) контакты базы имеют различные потециалы.

Для диффузионных емкостей также используются унифицированные ВФХ. Так, например, ВФХ диффузионной емкости эмиттерного перехода имеет вид:

,

где — дифференциальная проводимость перехода (в рабочей точке, соответствующей данному временному шагу),

— время пролета электронов через активную базу в прямом направлении.

8.1.5. Резистивные элементы.

Сопротивления и суть линейные омические сопротивления тела коллектора и тела эмиттера. Они задаются в модели как параметры. Ввиду одномерной картины тока в эмиттере расчет сопротивления не представляет сложности:

.

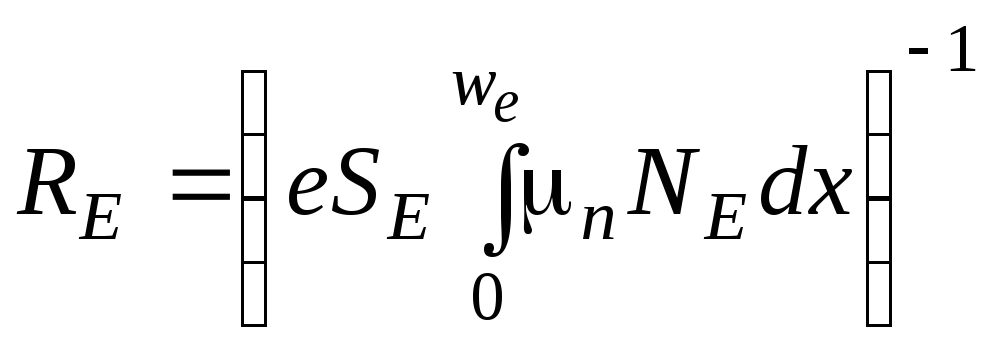Методика оценочного расчета сопротивления тела коллектора приведена в учебном пособии [3] (Старосельский В.И. Физика биполярных транзисторов. Бездрейфовые транзисторы. М.; МИЭТ, 1989, с. 36-38).

Сопротивление тела базы зависит от режима работы транзистора — при повышении уровня инжекции его величина уменьшается. В модели сопротивление разделено на две составляющие.

Первая из них () соответствует сопротивлениям пассивной и (если она есть) периферийной областей базы (рис.1.1а,б). Методика его оценочного расчета приведена в [3].

Вторая () характеризует сопротивление активной области базы (под эмиттером). Сумерное сопротивлени базы определено соотношением

где , — ток через R_B (рис. 8.1).

Параметр выбран так, что при  .

8.1.6. Латеральный р-п-р транзистор

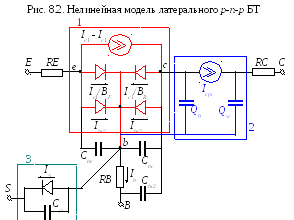
Нелинейная эквивалентная схема латерального р-п-р БТ (рис. 1.1в) представлена на рис. 8.2. Отличие модели латерального р-п-р БТ от рассмотренной модели п-р-п БТ состоит в следующем:

1. изменены полярности диодов и положительные направления токов;

2. подложкой латерального р-п-р БТ является область, соответствующая коллектору п-р-п БТ, что отражено подключением блока 3 к базовому электроду в (вместо колекторного с).

8.1. Модель Эберса-Молла

Как отмечалось в разделе 4, модель Эберса-Молла является частным случаем модели Гуммеля-Пуна, не учитывающим эффекты повышенного уровня инжекции в базе и коллекторе, модуляции толщины базы напряжениями и (эффект Эрли) и токов рекомбинации-генерации в р-п переходах. При этих допущениях эквивалентная схема упрощается и имеет вид, представленный на рис. 8.3.





I_e1 - I_c1

I_c1/B_R

E

e

c

S

I_e1/B_F

RE



C_js

I_S

Рис. 8.1. Нелинейная модель п-р-п БТ Эберса-Молла

1

3

C

RC

b

C_be

C_bc

C_bc2

RB



I_b

B

Поскольку все токи, инжектируемые через эмиттерный и коллекторный переходы одинаково зависят от соответствующих напряжений, ля их моделирования достаточно двух диодов.

При этом параметры и приобретают смысл прямого и инверсного коэффициентов базового тока и связаны с параметрами и (или и ) соотношениями

;

.

В этой модели накопление избыточных носителей заряда в коллекторе и базе описывается диффузионными составляющими емкостей (модель активного коллектора Кулла, описанная в разделе 6, не используется).

Заряд дырок в базе в модели Эберса-Молла считается равным равновесному (), поэтому сопротивление базы постоянно.

8.1.7. Температурные зависимости параметров

Для температурных зависимостей тепловых токов диодов (пропорциональных ) используются теоретические соотношения, в которые введены корректирующие параметры. Формулы, описывающие температурные зависимости тепловых токов, имеют вид:

,

где для коррекции используется параметр ХТ (по умолчанию ХТ = 3).

Контактные разности потенциалов, используемые в формулах ВФХ барьерных емкостей, зависят от температуры следующим образом:

.

Температурные зависимости барьерных емкостей при нулевом напряжении имеют вид:

.

Для описания температурной зависимости сопротивлений используется квадратичная аппроксимация:

,

где — температурные коэффициенты (по умолчанию равны 0).

9. Линеаризованная модель БТ

В малосигнальной линеаризованной эквивалентной схеме нелинейная зависимость тока I_e1 - I_c1 от напряжений , а также нелинейные ВАХ диодных элементов линеаризованы:

,

где — дифференциальная проводимость перехода В-Е,

— дифференциальная проводимость перехода В-С,

— проводимость коллектор-эмиттер.

Линейная эквивалентная схема БТ представлена на рис. 9.1.

В нормальном режиме проводимости и связаны с эффектом Эрли, и их величины малы (много меньше проводимости открытого эмиттерного перехода ).

Источники шума

Генераторы тока I_{N RЕ} , I_{N RС} , I_{N RB} моделируют тепловой шум соответствующих сопротивлений

— спектральная плотность этого шума [А²/ Гц].

Спектральная плотность теплового шума не зависит от частоты (белый шум).

Генератор тока I_{N ве} моделирует шумовые токи через эмиттерный переход. Эти токи включают дробовой шум, связанные с переносом через потенциальный барьер перехода дискретных зарядов е (белый спектр) и фликкер-шум (спектральная плотность пропорциональна ):

.

Здесь I_be2 — суммарный ток, связанный с инжекциейчерез эмиттерный переход (рис.8.1).

Генератор тока I_{N вс} моделирует шумовой ток через закрытый коллекторный переход. Фликкер-шум в нем не учитывается:

.