1) Рекомбинация в базе незначительна, и в стационарном состоянии электронный ток в базе не зависит от координаты х;

2) Коэффициент диффузии электронов в базе Dn не зависит от координаты х;

3) Дырочный ток в базе мал: .

Все допущения в реальных транзисторах выполнены с высокой точностью.

Согласно допущению 1 div j_n = 0. Таким образом, уравнение для тока, не зависящего отх, является 1-м интегралом уравнения непрерывности.

Токи электронов и дырок:

, (3.1)

где S_E— площадь эмиттерного перехода (знак «-» связан с тем, что положительное направление токаI_nна рис. 3.1 противоположно осих).

Напряженность электрического поля найдем из условия :

;. (3.2)

Подстановка (3.2) в (3.1) дает:

.

Умножив это уравнение на eS_E, получим:

. (3.3)

Это уравнение проинтегруем по всей базе (от х=х₁дох=х₂на рис. 2.1), учитывая, что согласно принятым допущениямI_nиD_nне зависят отх:

.

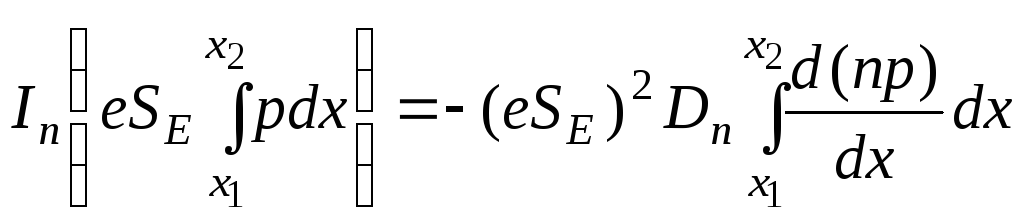
В левой части уравнения в скобках — полный заряд дырок в базе

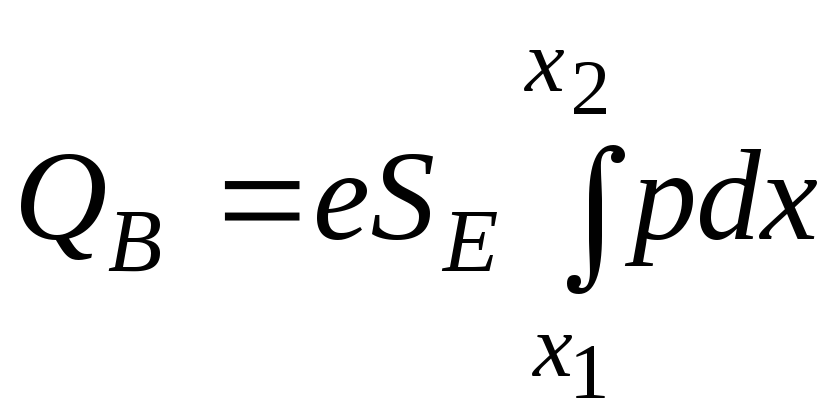
. (3.4)

В правой части:

;

(эти граничные условия следуют из постоянства квазиуровней Ферми в эмиттерном и коллекторном переходах). Таким образом:

.

Это соотношение можно представить в виде:

,

или:, (3.5)

где , (3.6а), (3.6б)

, (3.7а), (3.7б)

, (3.8)

— (3.9)

равновесный заряд дырок в базе (при),

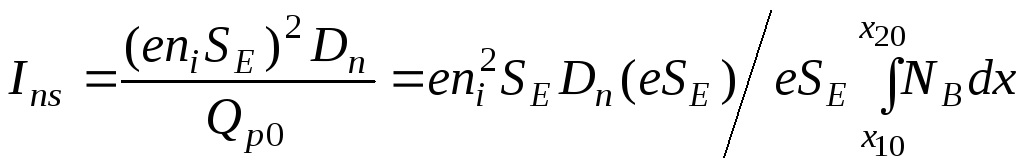
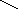
;— (3.10)

электронный тепловой ток эмиттерного перехода(совпадает с электронным тепловым током активной части коллекторного перехода), где

(Соотношение (3.10) дает и теория идеализированного транзистора).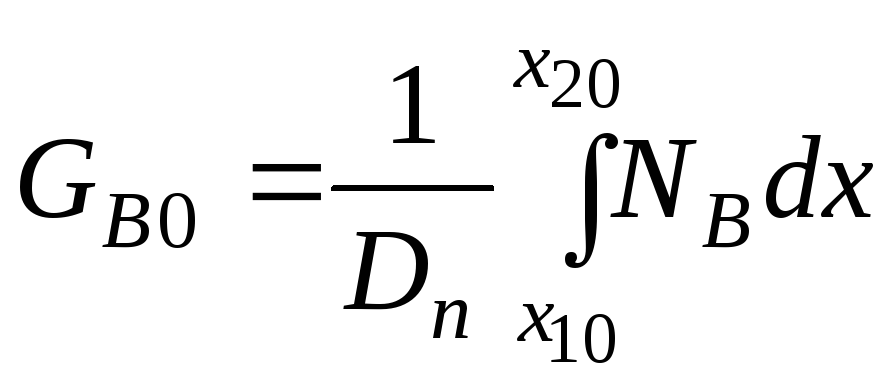

— число Гуммеля в базе.

Заряды Q_B0иQ_Bпоказаны на рис. 3.1. ЗарядQ_Bзависит от двух напряжений —и. Поэтому каждый из токовI_e1,I_с1также зависитот двух напряжений.

Распределение токов в БТ (рис. 2.1) и уравнения Гуммеля-Пуна (3.5) – (3.10) позволяют синтезировать модель биполярного транзистора.

4. Упрощенная модель Гумеля-Пуна

В этой модели делаются следующие допущения:

а) уровень инжекции в базе и коллекторе остается низким;

б) не учитывается модуляция толщины базы напряжениями и(эффект Эрли);

в) не учитываются токи рекомбинации-генерации в р-ппереходах.

При выполнении 1-х двух допущений заряд дырок в базе не изменяется под действием напряжений и, т.к.p(x)  p₀ (x) =N_B (x),, и:

Q_B=Q_B0 , т.е.(4.1)

При условии (4.1) из (3.6а,б) получим:

, (4.2а). (4.2б)

Каждый из токов I_e1, I_с1также зависит толькоот одного напряжения.

В пренебрежении токи рекомбинации-генерации (которые ~ ) оставшиеся составляющие тока базы зависят от напряжений на переходах так же, как токиI_be1, I_bс1 :

; (4.3а)

; (4.3б)

; (4.4)

(4.5)

(допущение о низком уровне инжекции в базе и коллекторе);

(4.6)

(уровне инжекции в эмиттере всегда остается низким).

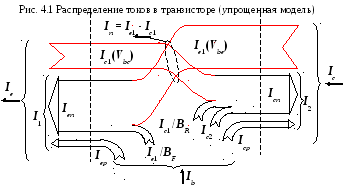
Распределение токов при сделанных допущениях представлено на рис. 4.1. Из рис. 4.1 и соотношений (4.2) - (4.6) следует, что токи, инжектированные через переходы В-Е и В-С, определяются соотношениями:

;

.

Таким образом, отношения

и

являются постоянными, не зависящими от режима работы транзистора, и могут использоваться какпараметрымодели. Параметрыиимеют смыслнормального и инверсного коэффициентов передачи тока.

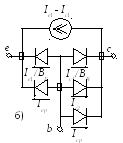
Два подхода к моделированию БТ иллюстрируются рисунком 4.2.

Рис. 4.2. Два подхода к моделированию БТ:

а - Эберса-Молла; б,в – Гуммеля-Пуна

а)

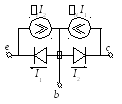
Модель Эберса-Молла (рис. 4.2а) использует коэффициенты ив качестве параметров. В модели Гуммеля-Пуна (рис. 4.2б) каждая составляющая базового тока моделируется отдельным диодным элементом.

Примечание: в модели Г-П параметры В_F и B_R не есть нормальный и инверсный коэффициенты усиления тока базы! Практически В_{F, R} > 1000.

При сделанных выше допущениях модели Эберса-Молла и Гуммеля-Пуна эквивалентны. Модель Эберса-Молла очень удобна для оценочных расчетов, т.к. параметры иимеют ясный электротехнический смысл. Модель Гуммеля-Пуна обладает большей гибкостью, позволяющей существенно улучшить ее точность за счет отказа от ряда принятых допущений.

Например, не представляет трудностей учет токов рекомбинации-генерации в р-ппереходах (допущение 3) путем добавления в цепи база-эмиттер и база-коллектор диодных элементов с соответствующими ВАХ (отлтчными от ВАХ других диодов). То же можно сделать и в модели Эберса-Молла, однако при этом параметрыипотеряют смысл коэффициентов передачи тока.

Резервы модели Гуммеля-Пуна состоят в возможности учета эффектов высокого уровня инжекции и эффекта Эрли (допущения 1 и 2), что в модели Эберса-Молла принципиально невозможно.