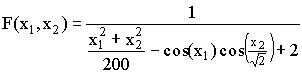1.2.10. Проверка работы комплекса на контрольных примерах

После проведения тестирования и отладки отдельных модулей комплекса встала задача проверки его функционирования в целом, т.е. проверки правильности получаемых результатов на контрольных примерах. В качестве начального примера была взята простейшаю функция y=2-(x + 4.6)^2. Переменная x меняла своё значение на интервале [-5; 0]. Оптимизация проводилась по двум направлениям – максимум и минимум. Аналитически легко показать, что максимум функции достигается при значении x -4.6 и равен 2. Минимум на этом отрезке достигается в 0 и равен -19.16. Модель, построенная для этого примера, показана на рис. 1.21

Рис. 1.21 Вид модели и значение переменных для контрольного примера

Результат вычислений, сохранённый в файл, оказался совершенно точным, что и не удивительно для такого простого примера. Ниже преведены содержания файлов для поиска максимума на отрезке и минимума.

Для максимума:

Время поиска: начало – [06.03.2005 20:37], конец – [06.03.2005 20:37], затрачено – 0 минут. Найденное наилучшее значение целевой функции = 2.0000 аргумент функции ($x) = -4.6000 Вероятность мутации = 0.0001 Вероятность кроссовера = 0.4500 Число точек кроссовера = 1 Критерий останова: отношение значений функции приспособленности для лучших особей в двух соседних популяциях = 0.0010 или число поколений составит 500 Направление оптимизации: максимум Поиск решения завершён. Причина: Найдено решение Число поколений составило 8

Для минимума:

Время поиска: начало – [06.03.2005 20:42], конец – [06.03.2005 20:42], затрачено – 0 минут. Найденное наилучшее значение целевой функции = -19.1600 аргумент функции ($x) = 0.0000 Вероятность мутации = 0.0001 Вероятность кроссовера = 0.4500 Число точек кроссовера = 1 Критерий останова: отношение значений функции приспособленности для лучших особей в двух соседних популяциях = 0.0010 или число поколений составит 500 Направление оптимизации: максимум Поиск решения завершён. Причина: Найдено решение Число поколений составило 7

Затем работа комплекса была протестирована на этом же самом примере, только отрезок, на котором осуществлялся поиск решения, был изменён на [-3; 1]. Комплекс успешно отработал и с таким вариантом. Полученное решение также оказалось точным.

После проверки работоспособности на простых примерах было решено сразу опробовать работу комплекса на специальных задачах, т.е. на задачах, используемых для проверки работы генетических алгоритмов. В качестве такой тестовой задачи была выбрана функция Гривонка (Griewank) [13]. Данная функция зависит от двух переменных и имеет один глобальный и множество локальных экстремумов. Аналитическое выражение для этой функции имеет следующий вид:

(1.1)

а значения переменных x₁ и x₂ принадлежат отрезку [-20; 20]

На рис. 1.22 представлен вид модели для данной функции

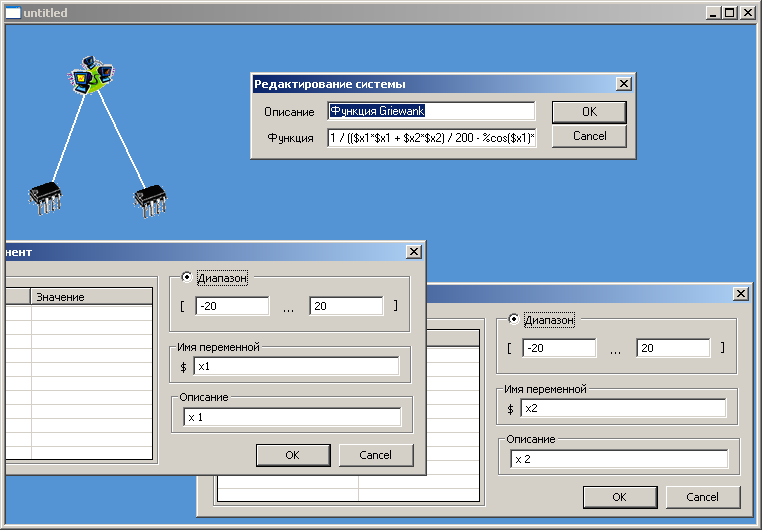
Рис 1.22 Вид модели и значение переменных для функции Griewank

Комплекс хорошо справился с задачей оптимизации данной системы (т.е. с задачей поиска значения глобального экстремума и значений аргументов функции, при которых этот экстремум достигается). Результаты оптимизации представлены ниже:

Время поиска: начало – [09.03.2005 18:06], конец – [09.03.2005 18:07], затрачено – 1 минут. Найденное наилучшее значение целевой функции = 0.9993 x 1 ($x1) = 0.0002 x 2 ($x2) = -0.0001 Вероятность мутации = 0.141 Вероятность кроссовера = 0.56 Число точек кроссовера = 1 Критерий останова: отношение значений функции приспособленности для лучших особей в двух соседних популяциях = 0.0003 или число поколений составит 300 Направление оптимизации: максимум Поиск решения завершён. Причина: Найдено решение Число поколений составило 37