Задача № 2 Построение статистических графиков

Рис. 1. Гистограмма и полигон

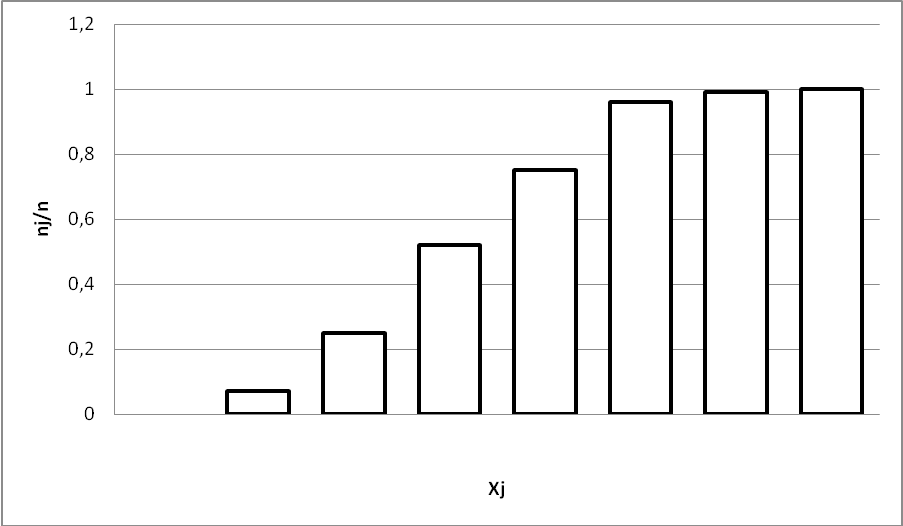
Рис. 2. Кумулятивная кривая

Задача № 3 Проверка гипотезы о принятом законе распределения

По данным примера 1 проверить гипотезу о законе распределения слу­чайной величины , используя критерий, результа­ты измерений которой представлены выборкой объемомn=100, ΔX=1,369, ,

Номер разряда	Середина разряда	Частота		Нормированные середины
1	52,32	7	-5,88	-1,84	0,0734	0,0230	5,52	0,395
2	54,72	18	-3,48	-1,09	0,2203	0,0691	16,57	0,123
3	57,12	27	-1,08	-0,34	0,3765	0,1180	28,33	0,062
4	59,52	23	1,32	0,41	0,3668	0,1150	27,60	0,766
5	61,92	21	3,72	1,17	0,2012	0,0631	15,14	2,271
6	64,32	3	6,12	1,92	0,0632	0,0198	4,75	-
7	66,72	1	8,52	2,67	0,0113	0,0035	0,85	-
	-	100	-	-	-	-	-	3,616

Нормированные середины рассчитываются по формуле:

.

Затем для каждого значение находят значение функции плотности вероятностей.

По найденному значению рассчитывают плотность вероятности физической величины теоретической функции распределения в единицах этой величины:

Определяют ту часть ту часть имеющихся наблюдений, которая теоретически должна быть в каждом из интервалов( n-общее число наблюдений):

Если в какой либо интервал теоретически попадает меньше пяти наблюдений, то в обеих гистограммах его соединяют с соседним интервалом. После этого определяют число степеней свободы

,

где - общее число интервалов, - число укрупненных интервалов.

Затем вычисляют интервальные значения критерия Пирсона

И величину .

Для нахождения граничных значений критерия определяют число степеней свободы:

= 7-1-2-2=2,

где =7 – число разрядов, =2 – число связей, накладываемое законом распределения, =2 – число укрупненных интервалов.

При =2 и уровне значимости по таблице П.2 приложения находят граничные значения критерия

Гипотеза о совпадении экспериментального и теоретического законов распределения принимается, так как . 3,525 входит в интервал (0,103; 5,991).

Рис. 3. Гистограмма равномерного распределения

Задача № 4 Проверка гипотезы о равномерном распределении по критерию

Случайная величина называется равнораспределенной на интервале , если ее плотность вероятности на этом интервале постоянна, а вне его равна нулю, т.е.

Где a и b- границы интервала возможных значений случайной величины.

В результате обработки ряда результатов измерений n=100 с размахом R= 67,76-51,12=16,64, с принятым числом интервалов q=7 и шириной интервала ΔX= R/q = 16,64/7 = 2,4, получены статистические характеристики = 59,44 и 4,7542.

Определяем границы интервала :

Определяем вероятности попадания случайной величины для эмпирического распределения:

№	Границы раздела
1	51,12	53,52	7	0,14	0,98	0,397
2	53,52	55,92	18	0,15	2,7	0,123
3	55,92	58,32	27	0,15	4,05	0,062
4	58,32	60,72	23	0,15	3,45	0,767
5	60,72	63,12	21	0,15	3,15	2,268
6	63,12	65,52	3	0,15	0,45	0,645
7	65,52	67,76	1	0,13	0,13	0,026
			100			4,289

Теоретическая частота для равномерного закона определяется по формуле

Определяем критерий

Число степеней свободы

При и уровне значимости по таблице П.2 приложения находят граничные значения критерия :

Так как не входит в интервал (0,711; 9,488), то гипотеза о равномерном законе распределения не принимается.