5. Продольная сила. Напряжения и деформации

Продольная сила N на участке равна сумме сил слева (или справа) от участка. Удобно рассчитывать N от свободного конца, чтобы не вычислять реакцию опоры.

Абсолютное удлинение ΔL стержня с длиной L и площадью сечения А равно

ΔL = N·L/(E·A). Часто встречается круглое сечение A=π·d²/4.

Продольная деформация ε на участке равна ε= N·/(E·A).

Знак деформации или удлинения (растягивающая или сжимающая) зависят от знака продольной силы.

Из гипотезы плоских сечений следует, что вдали от мест нагружения, резкого изменения  формы и размеров поперечного сечения нормальные напряжения σ при растяжении − сжатии прямолинейных стержней распределяются по площади поперечного сечения равномерно и равны σ=N/A.

Распределение напряжений по длине стержня, как и N, зависит от приложенных сил.

6. Испытание конструкционных материалов на растяжение и сжатие.

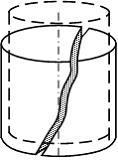
Материал является хрупким, если образец из него разрушается при очень малых остаточных деформациях. (от 0,1 до 5%). Вид разрушенн0го образца (чугун) после испытания представлен на рисунке.

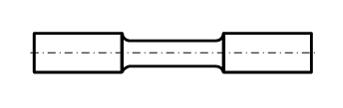Стальной образец, предназначенный для испытания на растяжение при статическом нагружении, имеет вид

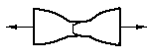Вид образца после разрушения представлен на рисунке (образуется шейка).

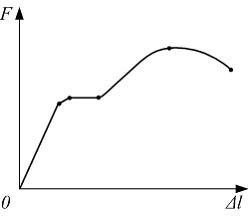
Диаграммой растяжения образца является диаграмма

После испытаний образца длиной L₀ на растяжение относительное остаточное удлинение при разрыве δ в процентах составляет δ=100·(L-L₀ )/ L₀, где L- длина расчетной (без шейки) части после разрыва.

Относительное остаточное сужение после разрыва в процентах определяется как отношение площади шейки при разрыве к начальной площади сечения образца, умноженное на 100.

Чем меньше δ и , тем более хрупкий материал.

Чугун и сталь–материалы изотропные. Примером анизотропного материала является древесина

7. Механические свойства материалов

На диаграмме растяжения участок ВС соответствует напряжению – предел текучести (),

точка D – пределу прочности - (), точка А – пределу пропорциональности.

Максимальная сила разрыва , которую может выдержать образец, .

До предела пропорциональности модуль упругости постоянный и равен .

Допускаемое напряжение [] для материала будет равно , где - нормативный коэффициент запаса.

Конструкционные материалы делятся на хрупкие и пластичные в зависимости от величины относительного остаточного удлинения при разрыве.

Коэффициентом Пуассона называется отношение относительной поперечной деформации к относительной продольной деформации, взятое по абсолютной величине.

Наклеп (нагартовка) – повышение упругих свойств  материала  в результате предварительного пластического деформирования.

Модуль сдвига - коэффициент пропорциональности между касательным напряжением () и угловой деформацией (), . Может быть определен при кручении круглого образца длиной L между крайними сечениями А и В и с моментом инерции сечения по формуле по известному углу поворота сечений .

Модуль сдвига связан с модулем упругости и коэффициентом Пуассона зависимостью .

8. Расчеты стержней на прочность и жесткость

Допускаемая нагрузка при растяжении или сжатии равна произведению допускаемого напряжения на площадь сечения.

Расчет на жесткость обычно , где F растягивающее (сжимающее) усилие, - допускаемое удлинение.

В задачах на фермы усилия в стержнях определяются их условия равновесия узлов.

Во многих задачах тестов усилие в стержнях находят из уравнения равновесия моментов относительно шарнирной опоры.

В стержнях из хрупких материалов необходимо отдельно определять допускаемые напряжения на растяжение и сжатие (бетон, чугун) и условие прочности .

ДЕ №3