14. Расчет балок на прочность

Расчет ведется по нормальным напряжениям (т.к. касательные для не тонкостенных балок значительно меньше нормальных).

Проверка на прочность по касательным напряжениям необходима в случае, если короткие балки нагружены перпендикулярно продольной оси силами, имеющими большое значение; материал балки плохо сопротивляется сдвиговым деформациям; ширина поперечного сечения балки в районе нейтральной оси мала.

Для пластичных материалов с одинаковой прочностью на растяжение и сжатие (сталей) .

Для хрупких материалов с разной прочностью на растяжение и сжатие (чугунов) расчет ведут отдельно для сжатых и растянутых слоёв.

Лучше работать на изгиб при данных условиях закрепления и нагружения будет балка, у которой сечение () изменяется в соответствии с с и изменением .

Полная проверка прочности балки при изгибе включает в себя проверку по нормальным напряжениям, проверку по касательным напряжениям и проверку по главным напряжениям.

Наиболее выгодным с точки зрения экономии массы является сечение, у которого при равенстве моментов сопротивления минимальное отношение площадей. При конкретном определяют и сравнивают площади соответствующих сечений. При сравнении двутавра и прямоугольника с высотой две ширины – отношение площадей (масс) в пользу двутавра.

В общем случае () на поверхности действуют только нормальные напряжения, в центре тяжести – только касательные, в произвольной точке – нормальные и касательные.

14. Перемещения при изгибе. Расчет балок на жесткость

В сечении возникают прогибы и углы поворота .

В опоре прогиб равен нулю. При . Прогиб, при прочих равных условиях, обратно пропорционален .

В общем случае прогиб и угол поворота в точке А определяются по способу Верещагина: , где - площадь эпюры момента от внешних сил, - значение момента от единичной силы, приложенной в точке при (- координата центра тяжести эпюры . Значение определяется также, но в точке прикладывается не единичная сила, а единичный момент.

В частных случаях:

• При равномерной погонной нагрузке на шарнирную балку в ее центре ;

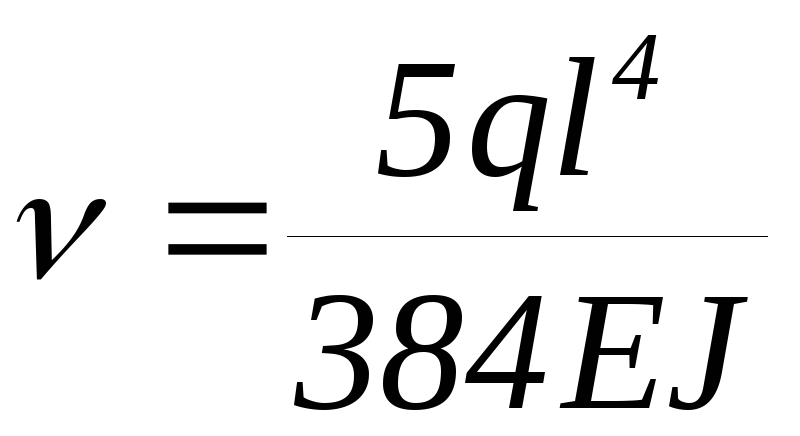• В точке приложения силы F на шарнирную балку в центре .

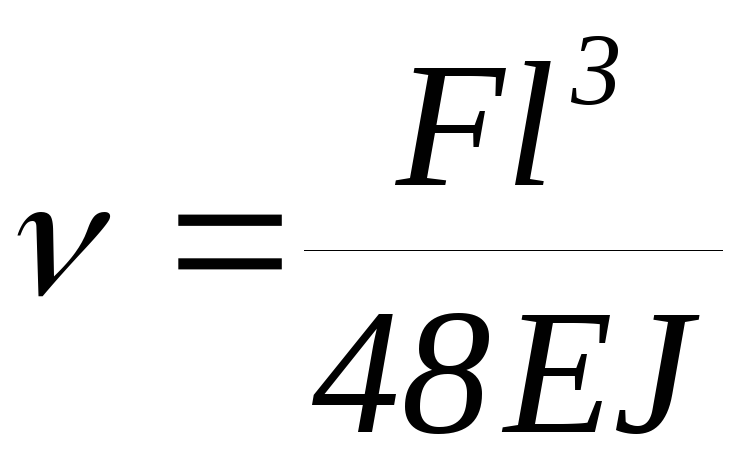• В точке приложения силы F на консольную балку на свободном конце ;

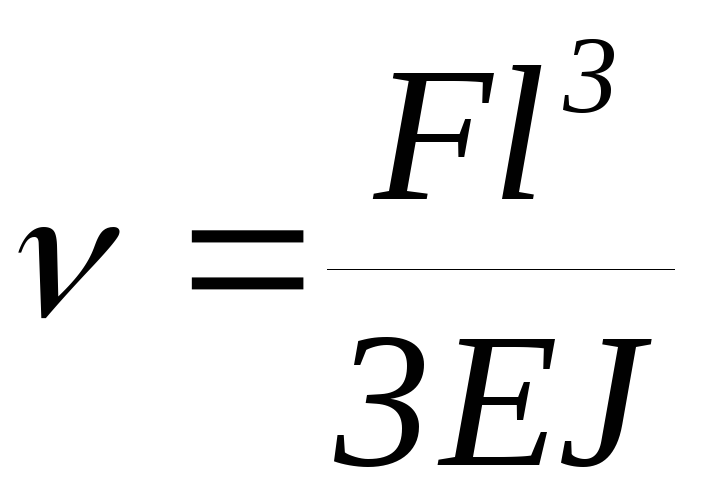• В точке приложения момента 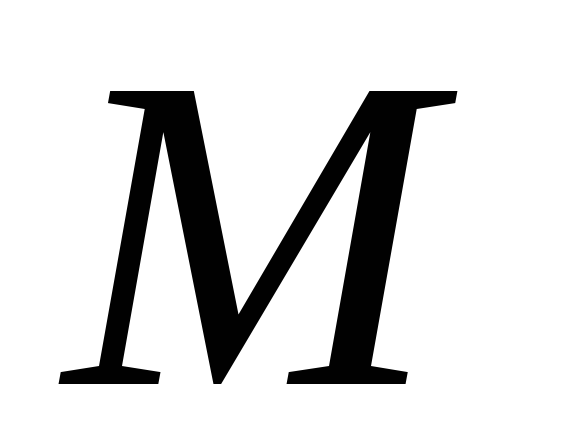на консольную балку на свободном конце .

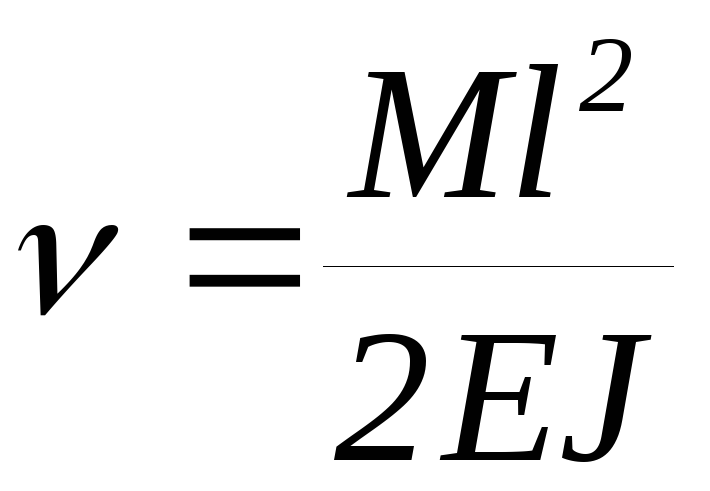Во многих простых задачах полезно изобразить вид прогиба и ответить на поставленные вопросы. Например:

О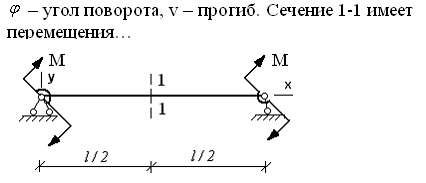чевидно, что в центре балки нет прогиба, но есть угол поворота.

Аналогично во многих других простых задачах.

ДЕ №7

14. Определение перемещений с помощью интегралов Мора. Правило Верещагина

Для определения перемещений (обобщенных) при плоском изгибе применяется интеграл Мора , вычисление которого по правилу Верещагина рассмотрено выше.

При поперечном изгибе более точная формула (с учетом сдвига от поперечной силы) -

Если стоит задача определения полного перемещения в точке, то следует найти перемещения в двух взаимно перпендикулярных направлениях , и вычислить .

26. Статическая неопределимость. Степень статической неопределенности

Степень статической неопределимости – число дополнительных связей , наложенных на систему сверх необходимого для достижения ее кинематической неизменяемости.

Связи иногда разделяют на внешние и внутренние . Внешние – связи от опор, внутренние – связи, образующие замкнутый контур.

Защемление - , шарнирно неподвижная опора - , шарнирно нподвижная опора - ,

Врезанный шарнир внутри контура - , вне контура - , замкнутый контур без шарнира - .

Число связей, при котором достигается кинематическая неизменяемость системы, носит название_ необходимого числа связей. В плоской конструкции число необходимых связей, обеспечивающих равновесие, равно 3.

В плоской конструкции .