8

ВЕКТОРЫ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ

Аналитическая геометрия изучает геометрические образы (точки, прямые, плоскости, поверхности и т.д.) при помощи аналитического метода. В основе этого метода лежит метод координат Рене Декарта (французский математик 1596-1650), позволяющий ввести соответствия между основными понятиями геометрии (точки, прямые, плоскости) и упорядоченными тройками вещественных чисел. Изучение свойств и взаимного расположения геометрических образов в аналитической геометрии сводится к изучению описывающих эти образы уравнений с привлечением методов алгебры и математического анализа.

I. Вектор, геометрическое определение вектора. Равные векторы.

Пусть на некоторой прямой заданы две точки A и B . Тем самым выделен отрезок AB этой прямой с концами в точках A и B.

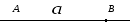
Можно считать, что точка A - начало отрезка, B - конец. Тогда мы зададим так называемый направленный отрезок, определяемый упорядоченной парой точек.

Определение . Направленный отрезок (упорядоченную пару точек) называют  вектором. Вектор обозначается или . Если точки A и B совпадают, то говорят, что вектор нулевой или нуль-вектор .

Расстояние между началом и концом вектора называется его  длиной или модулем и обозначается .

В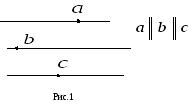 екторы называются  коллинеарными, если они имеют общую параллельную прямую. При совмещении начал коллинеарных векторов они оказываются лежащими на одной прямой.

В екторы называются  компланарными, если они параллельны одной и той же плоскости. При совмещении начал компланарных векторов они оказываются лежащими в одной плоскости.

Теперь можно ввести следующее определение: два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.

, если

, хотя но

Из определения равенства векторов следует, что каждый вектор можно перенести в любое место параллельно самому себе и не изменить его. Тем самым мы ввели так называемый свободный вектор, задать который - значит задать его модуль и направление. Многие физические величины характеризуются не только числовым значением, но и направлением, и, следовательно, являются векторными (сила, скорость, перемещение, магнитная индукция...).

II. Линейные операции над векторами, их свойства.

Понятие о линейном пространстве.

К линейным операциям над векторами относятся сложение векторов и умножение вектора на скаляр.

Сложение двух векторов выполняется по правилу параллелограмма:  сумма  двух векторов представляет собой диагональ параллелограмма, построенного на равных им векторах.

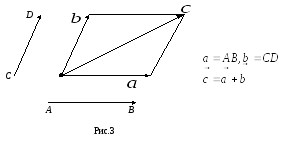
Сумма нескольких векторов определяется как вектор, замыкающий ломаную линию, звеньями которой служат векторы-слагаемые, и направленный из начала первого вектора в конец последнего.

Определение: произведением вектора на вещественное число называется

такой вектор , что 1)

2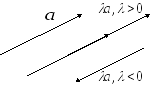) вектор коллинеарен ,

3) векторы и направлены одинаково,

если ,

и противоположно, если :

,если , ,если .

Вектор называется противоположным вектору . Сумма двух противоположных векторов равна нулевому вектору: .

Вычитание векторов - операция, обратная сложению:

Перечислим свойства введенных нами линейных операций:

1 ) коммутативность сложения: ;

2) ассоциативность сложения: ;

3) существование нуль-вектора: ;

4) существование противоположного вектора: ;

5) дистрибутивность сложения по отношению к умножению на число:

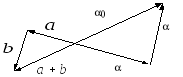
6) дистрибутивность сложения:

A B C D E

7) ассоциативность умножения:  т.к.

8) существование единицы:  это следует из определения

операции умножения.

Пространство, для элементов которого вводятся операции сложения и умножения на число, обладающие свойствами (1)-(8), называют линейным (векторным) пространством. Элементы линейного пространства обычно называют векторами.

III. Разложение вектора по базису. Координаты вектора.

Пусть заданы векторы и числа  Составим комбинацию из этих векторов, используя только введенные линейные комбинации сложения и умножения вектора на число. В самом общем случае она имеет вид: . Такие комбинации называются линейными комбинациями векторов , а числа - коэффициентами линейной комбинации.

Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам.

Пусть дан ненулевой вектор . Покажем, что любой коллинеарный ему вектор может быть представлен в виде единственным образом.

По определению операции умножения вектора на число векторы и коллинеарны, следовательно, коллинеарны и векторы и . Одинаковое направление векторов и обеспечивается выбором знака числа . Наконец, из равенства модулей равных векторов следует, что . Единственность представления следует из того, что при умножении вектора на другое число получается новый вектор: при .

Теорема 1. Любой вектор на плоскости может быть разложен по двум неколлинеарным векторам и единственным образом.

Доказательство: В общем случае отложим все три вектора из общей точки О. Из конца вектора (точки А) проведем прямые АР и AQ, параллельные векторам и . Тогда по правилу параллелограмма

.

Вектор коллениарен вектору и, следовательно, единственным образом может быть представлен в виде . Вектор коллинеарен вектору , поэтому . Тогда - единственное разложение вектора по векторам и .

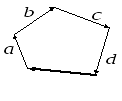
Неколлинеарные векторы и , взятые в определенном порядке, называются базисом на плоскости, а коэффициенты линейной комбинации ₁ и ₂ - координатами вектора в базисе и .

Т

.

еорема2: любой вектор единственным образом раскладывается по трем фиксированным некомпланарным векторам:

Некомпланарные векторы образуют базис пространства. Коэффициенты разложения называют координатами вектора в базисе .

Таким образом, в пространстве с выбранным базисом нам удалось каждому вектору поставить в соответствие тройку чисел - его координат. Теперь при выполнении введенных линейных операций над векторами можно заменить геометрические построения аналитическими выражениями.

Пусть

тогда

и

Таким образом, при умножении вектора на число все его координаты умножаются на это число, а при сложении векторов складываются их соответствующие координаты, если они определены относительно одного и того же базиса.

IV. Линейная зависимость векторов. Размерность линейного пространства.

Запишем линейную комбинацию векторов Она называется тривиальной, если все ее коэффициенты одновременно равны нулю, то есть , и нетривиальной, если хотя бы один из коэффициентов отличен от нуля.

Определение: векторы называют линейно зависимыми, если можно найти их нетривиальную комбинацию, равную нулю:

при .

Определение: если для векторов обращается в нуль только их тривиальная комбинация, то такие векторы называют линейно независимыми:

при .

Векторы линейно зависимы, если хотя бы один из них можно представить как линейную комбинацию остальных. Пусть , тогда

Тогда на основании доказанных выше теорем оказывается, что линейно зависимыми являются любые два коллинеарных вектора (), любые три компланарных вектора () и любые четыре вектора в пространстве (). В свою очередь линейно независимыми всегда являются базисные векторы, т.е. два неколлинеарных вектора на плоскости и три некомпланарных вектора в пространстве.

Определение: количество векторов, образующих базис линейного пространства, называют размерностью этого пространства.

Размерность определяется наибольшим числом линейно независимых векторов пространства. Линейное пространство, имеющее размерность n, принято обозначать .

V. Системы координат.

Определение: декартовой системой координат называются совокупность точки и базиса.

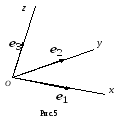
Точка О называется началом координат,

Ox,Oy,Oz - координатными осями,

Oxy,Oyz,Oxz - координатными плоскостями.

Декартова система координат, базисные векторы которой взаимно перпендикулярны и имеют единичные длины, называется декартовой прямоугольной системой, а ее базис – ортонормированным.

Координатами точки А в выбранной cистеме координат называются координаты радиус-вектора этой точки в этой системе координат.

Если заданы координаты точек и , то можно найти выражение для координат вектора .

Из рисунка 6 следует, что , тогда . Если , то - координаты вектора .

На практике пользуются и другими системами координат, например, косоугольной декартовой, полярной, цилиндрической, сферической и др.