Геологи(1 курс). Математика. / Тема_03_ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЕ

20

ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЕ

I. Ориентация тройки векторов.

Три некомпланарных вектора в пространстве образуют упорядоченную тройку, если принято соглашение, что один из них является первым , другой - вторым (), а оставшийся - третьим () .

Каждой упорядоченной тройке (базису) приписывается ориентация - правая и левая.

Правый базис Левый базис

Рис.1

Упорядоченная тройка векторов называется правой, если из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки. В противном случае тройка называется левой.

Если рассматривать три ортонормированых базиса, среди которых один базис образует правую тройку, а другой - левую, то третий может быть совмещен либо с первым, либо со вторым. Тогда все ортонормированные базисы могут быть разбиты на два класса: правых и левых троек. В дальнейшем рассматриваемые базисы будем считать правыми.

II. Определение и геометрические свойства векторного произведения.

Определение: векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:

1)

2)

3) векторы образуют правую тройку.

Рис.2

Если хотя бы один из векторов или нулевой, то по определению их векторное произведение равно нулю.

Пример: Пусть - правый ортонормированный базис.

Тогда

Если -левый ортонормированный базис то

Теорема : необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Доказательство : 1) необходимость: если , то и .

2) достаточность: если , то либо , либо , тогда и - коллинеарны по определению; либо .

Из определения векторного произведения следует, что модуль векторного произведения равен площади параллелограмма, построенного на перемножаемых векторах.

(2)

III. Алгебраические свойства векторного произведения.

Векторное произведение обладает следующими алгебраическими свойствами:

1) антикоммутативность:;

2) ассоциативность: ;

3) дистрибутивность: ;

4) для любого вектора : .

Пример : найти площадь параллелограмма, построенного на векторах

и ,

если .

Решение: ;

IV. Определение смешанного произведения. Его свойства.

Определение: смешанным произведением векторов , и называется число, равное скалярному произведению вектора на векторное произведение векторов и : .

Смешанное произведение трех некомпланарных векторов равно объему параллелепипеда, построенного на этих векторах. Оно положительно, если тройка векторов - правая, и отрицательна, если - левая.

Знак смешанного произведения определяется знаком . Поскольку тройка векторов по определению правая, то смешанное произведение положительно, когда вектор направлен в ту же сторону от плоскости векторов и , что и , т.е. тройка векторов - правая. Аналогично можно показать, что смешанное произведение левой тройки векторов отрицательно.

(3)

S - площадь основания

H - высота

Рис.5

Если - ортонормированный правый базис, то , если - ортонормированный левый базис, то .

Теорема: Смешанное произведение равно нулю в том и только в том случае, когда сомножители компланарны.

Доказательство :

, если

1) один из векторов нулевой, но тогда - компланарны;

2) и коллинеарны и - компланарны;

3) ,тогда - компланарны (лежат в одной плоскости).

В силу свойств смешанного произведения , т.к. в левой и правой частях равенства стоят выражения, равные объему одного и того же параллелепипеда.

Поскольку скалярное произведение коммутативно, а векторное -антикоммутативно, то имеет место соотношение:

Покажем, что смешанное произведение обладает свойством линейности:

вследствие линейности скалярного произведения. Эти соотношения для остальных сомножителей доказываются аналогично после перестановок.

V. Выражение векторного и смешанного произведения в декартовых координатах.

Пусть векторы заданы своими координатами в ортонормированном правом базисе , т.е. имеют место соотношения:

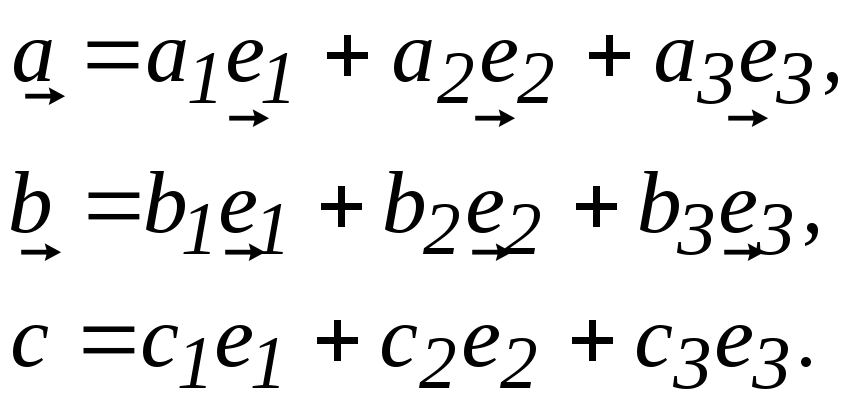
Получим выражение для координат вектора .

Здесь учли, что для ортонормированного базиса:

Тогда

или i,j,k - тройка 1,2,3; 3,1,2; 2,3,1.

Смешанное произведение векторов также может быть выражено через координаты этих векторов в ортонормированном базисе

Для запоминания последних двух формул удобно пользовать символ определителя.

Пусть имеется таблица, составленная из четырех чисел .

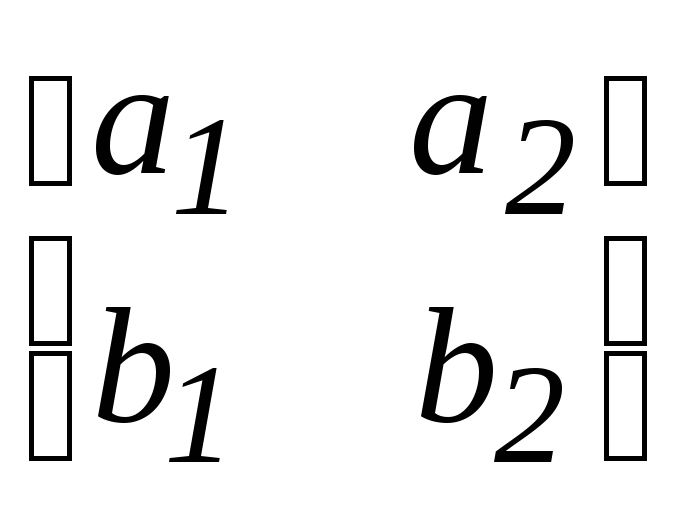Такая таблица называется матрицей второго порядка. Число - называется определителем (детерминантом) данной матрицы и обозначается:

Для матрицы третьего порядка, составленной из девяти чисел, можно вычислить определитель третьего порядка:

Тогда

, ,

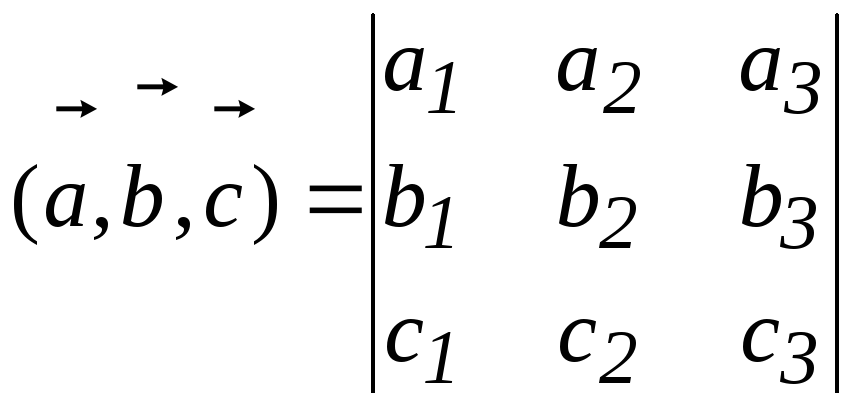т.е. векторное произведение двух векторов может быть представлено как определитель третьего порядка, у которого в первой строке стоят базисные векторы, а во второй и третьей строках – координаты перемножаемых векторов. Смешанное произведение представляется как определитель третьего порядка, строки которого образованы координатами перемножаемых векторов.

Пример . Вычислить объем параллелепипеда, построенного на векторах и , и длину высоты, опущенной на основание .

Решение:

, , .

; .

.