Геологи(1 курс). Математика. / Тема_09_ПРЕДЕЛ ФУНКЦИИ

72

ПРЕДЕЛ ФУНКЦИИ

I. Определение предела функции в точке.

Введем понятие предела функции. Для этого рассмотрим в качестве примера функцию

.

Областью определения данной функции является множество вещественных чисел за исключением x=1 , то есть при x=1 функция не определена. На всей области определения значение функции можно вычислить как y=1+x. На рисунке представлен график рассматриваемой функции. Из графика видно, что если значения x близки к 1 , но , то значения функции близки к 2, хотя y2.

Точный смысл этого утверждения заключается в следующем: возьмем малое число и найдем такое число , что для всех x из

 -окрестности точки x=1 значения функции отличаются от числа 2 на величину, меньшую .

Геометрически это означает, что нужно найти такое , что для всех x из интервала (1-, 1+ ) соответствующие точки графика функции лежат в горизонтальной полосе, ограниченной прямыми y=2- и y=2+ . В данном примере можно взять  .

В этом случае говорят, что функция стремится к двум при x1, а число 2 называют пределом функции y(x) при x1 , и пишут

.

Определение предела по Коши: число A называют пределом функции y=f(x) в точке a , если эта функция определена в некоторой окрестности точки a, за исключением, быть может, самой точки a, и для каждого >0 найдется такое >0, что для всех x, удовлетворяющих условию , выполняется неравенство :

Таким образом, число A является пределом функции f(x) при xa, если для любой  -окрестности числа A можно найти такую  -окрестность числа a, что для всех x из этой  -окрестности соответствующие значения функции лежат в

 -окрестности числа A .

Примеры:

1) Функция не определена при x=0 , но имеет предел при x0 .

,

так как .

2) Функция не определена при x=0 и не имеет предела в этой точке, так как при x0 функция попеременно принимает все свои значения от -1 до +1.

3) Функция y=sinx определена при x=0 и имеет предел в этой точке .

II. Различные типы пределов функций.

Для функции непрерывного аргумента различают односторонние конечные пределы, бесконечные пределы в конечной точке и пределы в бесконечности.

Односторонние конечные пределы функции определяют следующим образом:

число A₁ называют пределом слева функции f(x) в точке a, если и записывают ;

число A₂ называют пределом справа функции f(x) в точке a, если и пишут

Числа A_! и A₂ описывают поведение функции соответственно в левой и правой полуокрестностях точки a.

Рассмотрим в качестве примера функцию .

При x=0 эта функция не определена. Найдем односторонние пределы функции в точке x=0 .

Для существования обыкновенного (двустороннего) предела функции в точке a необходимо и достаточно существование порознь и равенство двух односторонних пределов функции в этой точке:

, если

В рассмотренном выше примере пределы функции слева и справа в точке x=0 не равны.

Функция y=f(x) может иметь бесконечный предел в конечной точке: , если .

В этом случае функцию называют бесконечно большой при .

Геометрически определение бесконечного предела функции означает, что какое бы число M мы ни взяли, всегда найдется такая  -окрестность точки a, что точки f(x) для всех x из этой окрестности лежат вне горизонтальной полосы, ограниченной прямыми y= - M и y=M.

Например, если , то так как условия выполняются для всех .

Для функции непрерывного аргумента вводится понятие предела в бесконечности. Если то число A называют пределом функции при x, стремящемся к бесконечности и пишут 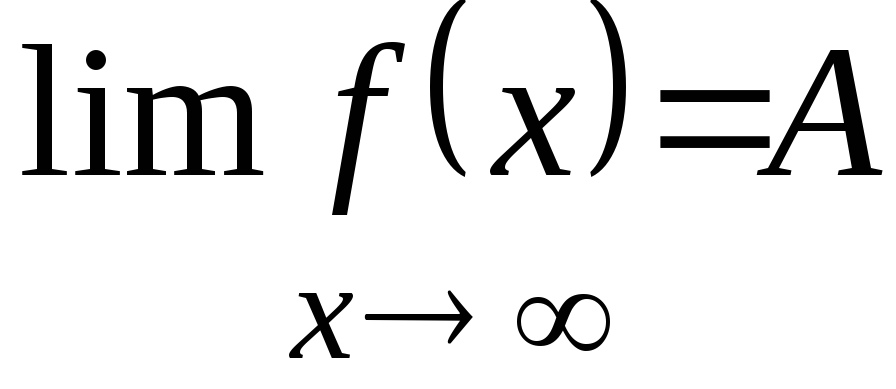. Например, .

III. Переход к пределу в неравенствах.

Укажем свойства функций, имеющих предел:

Свойство 1: если , где A - конечное число, то в некоторой окрестности точки a функция ограничена, то есть существует M>0 такое, что из окрестности точки a .

Доказательство: пусть  =1 , тогда существует такое , что выполняются неравенства

Свойство 2: пусть в окрестности точки a функции связаны неравенством причем , тогда .

Свойство 3: если в окрестности точки a функции u(x) и v(x) связаны неравенством , то

IV. Первый замечательный предел.

Первым замечательным пределом называют предел функции при .

Докажем, что .

Для этого воспользуемся свойством 2 пределов трех функций.

Покажем, что если и , то

Рассмотрим в координатной плоскости круг единичного радиуса с центром в точке O .

Пусть и . Построим точку C как

проекцию точки B на ось Ox и точку D как пересечение луча

OB и перпендикуляра к Ox, проведенного через A. Тогда

, так как

из подобия и .

Пусть S₁ - площадь , S₂ - площадь сектора AOB, S₃ - площадь . Тогда

.

Так как S₁ <S₂ <S₃ , то

(*)

Полученное неравенство справедливо и при , так как и - четные функции.

Таким образом, неравенство (*) справедливо при как слева, так и справа. Кроме того, , , тогда в соответствии со свойствами пределов

.

V. Теоремы о пределах. Неопределенные выражения.

Теорема 1. Предел алгебраической суммы конечного числа функций равен

сумме их пределов:

Теорема 2. Предел произведения конечного числа функций равен произведению их пределов:

Следствие: постоянный множитель можно выносить за знак предела:

Пример:

Теорема 3. Предел частного двух функций равен частному их пределов,

если предел знаменателя отличен от нуля:

Пример:

При вычислении пределов арифметических выражений по пределам функций , из которых они составлены, не всегда возможно. В этих случаях говорят, что возникают неопределенности следующих видов: Для нахождения пределов таких неопределенных выражений нужно учитывать конкретный вид функции

Примеры раскрытия неопределенностей:

1)

2. 

3.