82

Производная. Производные и дифференциалы высших порядков.

I. Скорость прямолинейного движения.

Рассмотрим задачу о движении материальной точки по прямой линии (см.рис.1). Пусть в момент времени t₀ точка занимала положение M₀ , а в момент

t - положение M на расстоянии S от M₀ . За время

точка из положения M переместится в положение M₁ , пройдя расстояние .

На отрезке движение точки характеризуется величиной средней скорости . Если считать путь, пройденный точкой, функцией времени, то расстояние можно найти как приращение функции S(t):

. Тогда

Однако на интервале t скорость точки может изменяться самым произвольным образом. При этом средняя скорость будет тем лучше характеризовать движение точки, чем меньше интервал . Если при существует предел средней скорости, то его называют мгновенной скоростью точки в данный момент t :

(1)

Из формулы (1) следует, что мгновенная скорость прямолинейного движения представляет собой предел отношения приращения пути к приращению времени , соответствующему , при

II. Определение производной.

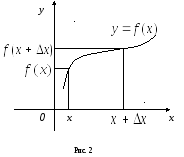Пусть задана функция y= f(x), определенная в некотором интервале. При каждом значении аргумента x в этом интервале функция y= f(x) имеет определенное значение. Если аргумент x получил приращение , то и функция y= f(x) получила некоторое определенное приращение

Если существует предел отношения при , то он называется производной функции f(x) в точке x и обозначается:

. (2)

Операция вычисления производной данной функции называется дифференцированием функции.

В соответствии с определением производная функции является функцией x, так как для каждого значения x предел, стоящий в правой части соотношения (2) имеет определенное значение.

Пример 1. Найти производную функции y= xⁿ , где , x>0 .

Зададим в точке x приращение аргумента и вычислим соответствующее приращение функции

Найдем

Таким образом, (xⁿ)= nx^n-1.

Пример 2. Пусть y= C . Тогда y=0 и y=C=0 .

Если сравнить соотношения (1) и (2), то можно отметить, что производную функции можно рассматривать как скорость изменения функции в заданной точке. В этом состоит механический смысл производной.

Пример 3. Найти скорость движения камня при свободном падении, если задан закон движения

Таким образом, V(t)= - gt - закон изменения скорости.

III. Геометрический смысл производной.

Рассмотрим в декартовой системе координат кривую, заданную уравнением y= f(x) . Причем функция y= f(x) определена и непрерывна на рассматриваемом интервале. Возьмем на этой кривой точку M₀ с координатами M(x₀ , f(x₀)). Зададим произвольное приращение аргумента x . Значению аргумента x₀+x соответствует точка на кривой M₁ (x₀+x, f(x₀+x)) .

Построим прямую линию M₀M₁ . Эта прямая называется секущей. Ее уравнение имеет вид y-f(x₀)=tg(x-x₀). Заметим, что - тангенс угла наклона прямой - угловой коэффициент секущей.

Пусть , тогда и , так как функция непрерывна в точке x₀, поэтому также стремится к нулю. Предельное положение секущей, когда точка M₁ совпадает с точкой M₀ (при ), называется касательной к кривой y= f(x) в точке M₀ . На рис.3 это прямая M₀T .

При секущая , поворачивается вокруг точки M₀, при этом изменяется угол , достигая предельного значения , соответствующего касательной M₀T .

Уравнение касательной к кривой M₀T имеет вид

Таким образом, угловой коэффициент касательной к кривой в точке M₀ равен значению производной рассматриваемой функции в данной точке. В этом состоит геометрический смысл производной.

Уравнение касательной к кривой y= f(x) в точке M₀(x₀,f(x₀)) имеет вид:

(3)

Можно показать, что уравнение прямой M₀N , перпендикулярной к касательной в точке M₀ и называемой нормалью к кривой, можно записать в виде:

, (4)

если только f`(x₀)0 .