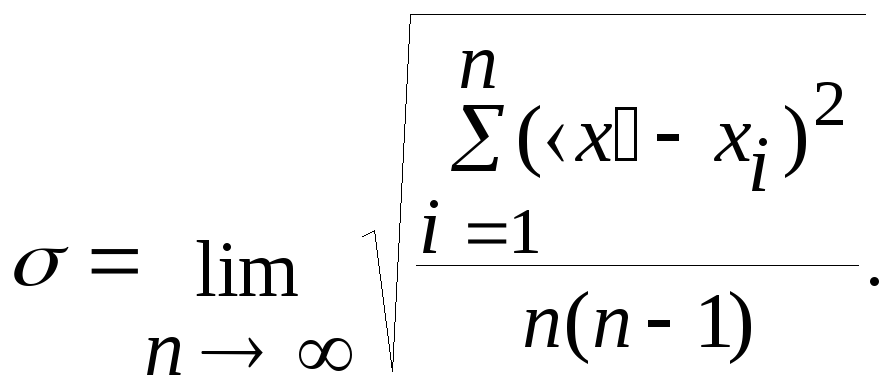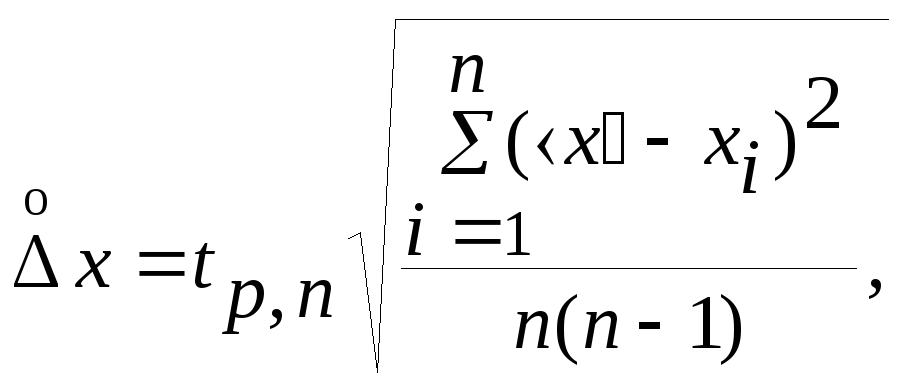8.2. Распределение Гаусса

Мы будем пользоваться только распределением Гаусса [1, с. 26], представленным на рисунке 8.1.1 кривой 4

,	(8.2.1)
где
	(8.2.2)

Эта формула распределения вполне приемлема и позволяет легко провести вычисления. Кроме того, оценки ошибок в большинстве случаев оказываются довольно грубыми, и эта неопределенность в их оценке полностью перекрывает ошибки, которые обусловлены произволом выбора в качестве функции распределения формулы (8.2.1). Правда, сказанное выше выполняется не всегда. Например, если результаты измерений дискретны и соответствуют ближайшим делениям шкалы прибора, пользоваться гауссовым распределением нельзя.

Перечислим основные свойства распределения Гаусса:

• Функция f(x) зеркально симметрична относительно истинного значения X измеряемой величины x.

• Площадь под кривой f(x) пропорциональна общему числу измерений. Коэффициент пропорциональности принято выбирать так, чтобы эта площадь равнялась 1; тогда

	(8.2.3)

• Точки перегиба кривой (8.2.1) удалены от X на ± σ. При этом доля результатов всех измерений, попадающая в интервал (- σ, + σ), составляет 68.3 %. В интервале (- 2σ, + 2σ) находится уже 95.4 % всех результатов. В теории вероятности σ называется средним квадратичным отклонением, а σ² – дисперсией, характеризующей разброс случайной величины (dispersio - рассеяние).

• Функция f(x)называется плотностью распределения и равна числу отсчетов, приходящихся на единичный интервал, так что f(x)dx равно числу попаданий измеряемой величины X в интервал от x до x + dx.

8.3. Метод Стьюдента

Наша задача состоит в том, чтобы, не выполняя большого числа измерений, найти среднее значение x, близкое к истинному значению X измеряемой величины, и погрешность измерений - полуширину доверительного интервала x, близкую к 2σ, как того требуют Государственные стандарты [2, 3]. Это делается по формулам Стьюдента (У. Госсет, Англия, 1908; Student – его псевдоним). Рекомендуется в качестве истинного значения X брать x, вычисляемое по формуле (5.2.1), а случайную ошибку оценивать по формуле

	(8.3.1)

где n – число измерений.

Коэффициенты Стьюдента t_p,n зависят от значения надежности p и числа измерений n. Величины этих коэффициентов для заданного p = 0.95 [2, 3] и различных n находят по таблице 1.1.1.

Проиллюстрируем эффективность методики Стьюдента при определении среднего значения и доверительного интервала по данным небольшого количества измерений на нашем примере с подсчетом числа шагов.

Для всей серии из n = 2080 испытаний (таблица 8.1.1) коэффициент Стьюдента t_p,n равен 2, и после весьма трудоемких вычислений по формулам (5.2.1) и (8.3.1) получаем следующее выражение:

X = (6410 ± 150) шагов	(p = 0.95).	(8.3.2)

Однако приведенный результат не является окончательным. В соответствии с излагаемыми далее – в параграфе 9.1 – правилами округления экспериментальных данных, предписывающими, сколько значащих цифр следует оставлять при оценке погрешности, выражение (8.3.2) следует записать в виде (9.1.2):

X = (6.41 ± 0.15)∙103 шагов	(p = 0.95).

Возвратимся к нашему примеру об измерении расстояния шагами. Для сопоставления результатов обработки большого числа измерений (8.3.2) с гистограммами и кривой распределения удобно отметить эти данные на числовой оси (рисунок 8.1.1, б) в том же масштабе, что и на рисунке 8.1.1, а. Среднее значение (5.2.1) покажем вертикальной черточкой, а доверительный интервал (8.3.1) – круглыми скобками. Из рисунка 8.1.1 видно, что, поскольку расчеты выполнены по очень большому количеству измерений, x действительно совпадает с абсциссой максимума кривой распределения, а границы доверительного интервала удалены от максимума вдвое дальше точек перегиба.

Если теперь из всей серии в 2080 испытаний произвольно, скажем, с помощью генератора случайных чисел, выбрать всего 5 значений x, получится приблизительно такой же результат. Пусть, например, выбраны числа x₁ = 6251, x₂ = 6368, x₃ = 6583, x₄ = 6483, x₅ = 6505. После обработки по Стьюденту получим

X = (6438 ± 163)  (6.41 ± 0.16)∙103 шагов	(p = 0.95).	(8.3.3)

Отметим эти данные, а также выбранные числа на оси x рисунка 8.1.1, в. Сравнивая выражения (1.1.6 – 1.1.8) и рисунки 8.1.1, а - 8.1.1, в, убеждаемся, что метод Стьюдента позволяет с весьма неплохой точностью находить интересующие нас величины по коротким сериям испытаний. Некоторое расхождение результатов вполне допустимо, особенно если вспомнить об экономии времени и усилий на измерения и обработку при сокращении количества опытов – в нашем примере с 2080 до 5!