
16.3. Распределение Максвелла
Вид функции распределения может быть установлен с помощью формальных рассуждений, не связанных с исследованием особенностей взаимодействия молекул газа между собой. Рассмотренный ниже подход был предложен Максвеллом в 1859 году.
Введем
пространство скоростей. Скорость
![]() любой
молекулы газа можно представить через
её проекции
любой
молекулы газа можно представить через
её проекции![]() ,
,![]() и
и![]() на
соответствующие оси системы координат
в пространстве скоростей. Если указанные
значения отложить по осям
на
соответствующие оси системы координат
в пространстве скоростей. Если указанные
значения отложить по осям![]() ,
,![]() и
и![]() прямоугольной
системы координат, то можно построить
пространство скоростей, каждая точка
в котором будет соответствовать
определенному набору проекций скорости
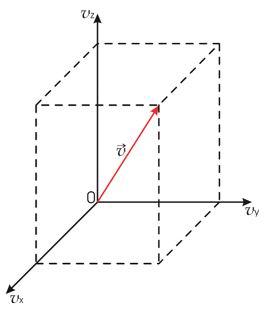
молекулы газа (см. рис. 16.2).
прямоугольной
системы координат, то можно построить
пространство скоростей, каждая точка
в котором будет соответствовать
определенному набору проекций скорости
молекулы газа (см. рис. 16.2).
|
|
|
Рис. 16.2. Пространство скоростей
|
Далее
сделаем предположение, что вероятности
попадания значений проекций скорости
молекулы
![]() ,
,![]() и
и![]() в
соответствующие интервалы
в
соответствующие интервалы![]() ,
,![]() и
и![]() не
зависят друг от друга, то есть значения
проекций скорости молекул на ортогональные
оси считаются статистически независимыми
величинами. Тогда по аналогии с формулой(16.10)
функцию распределения
не
зависят друг от друга, то есть значения
проекций скорости молекул на ортогональные
оси считаются статистически независимыми
величинами. Тогда по аналогии с формулой(16.10)
функцию распределения
![]() можно
представить в виде:
можно
представить в виде:
|
|
(16.24) |
где
![]() ,
,![]() и
и![]() -
функции распределения значений
соответствующих проекций скорости
-
функции распределения значений
соответствующих проекций скорости![]() ,
,![]() и
и![]() ,
причем вид этих функций должен быть
одинаковым, так как все оси системы
координат в пространстве скоростей
равноправны.
,
причем вид этих функций должен быть
одинаковым, так как все оси системы
координат в пространстве скоростей
равноправны.
Максвел
получил, что
,
функция
![]() распределения
значений проекции скорости
распределения
значений проекции скорости![]() определяется выражением:
определяется выражением:
|
|
(16.25) |
а функция распределения молекул газа по скоростям соответственно имеет вид
|
|
(16.26) |
или
|
|
(16.27) |
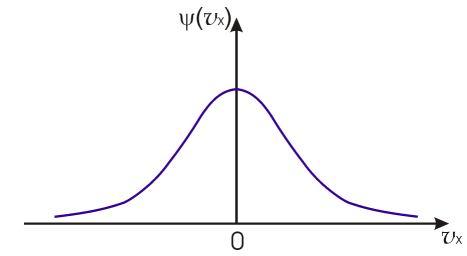
Функции (16.25)и(16.26)(или(16.27)) называются функциямираспределения Максвелла. Качественно вид функции (16.25), изображенной на рис. 16.3, совпадает с нормальным законом распределения Гаусса, описывающим распределение ошибок измерений случайной величины.
|
|
|
Рис. 16.3. Распределение Максвелла
|
Кроме
полученного выше распределения Максвелла
![]() часто
при проведении расчетов используется
распределение по абсолютным значениям
скоростей молекул газа.
часто
при проведении расчетов используется
распределение по абсолютным значениям
скоростей молекул газа.
|
|
(16.28) |
называется
функцией распределения
Максвелла по абсолютным значениям
скоростей,
и она показывает вероятность того, что
величина скорости имеет значения от
![]() до
до![]() .
.
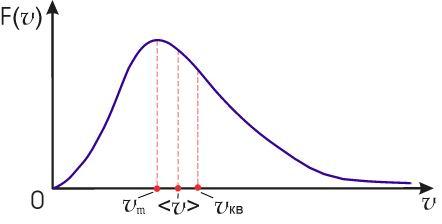
На
рис. 16.4 изображен график функции
распределения
![]() .
Максимум этой функции соответствует
наиболее вероятному значению скорости
молекул газа
.
Максимум этой функции соответствует
наиболее вероятному значению скорости
молекул газа![]() ,
которую можно определить, приравняв к
нулю производную от функции
,
которую можно определить, приравняв к
нулю производную от функции![]() :
:
|
|
(16.29) |
Отсюда
следует, что кроме случаев когда
![]() и
и![]() ,
соответствующих минимуму функции
,
соответствующих минимуму функции![]() ,
имеется решение
,
имеется решение
|
|
(16.30) |
дающее выражение для наиболее вероятной скорости молекул газа.
|
|
|
Рис. 16.4. Распределение Максвелла по абсолютным значениям скоростей
|
Кроме
наиболее вероятной скорости, функция
![]() позволяет
найти среднюю скорость
позволяет
найти среднюю скорость
|
|
(16.31) |
и среднее значение квадрата скорости
|
|
(16.32) |
Вычисление интегралов окончательно дает выражения для средней скорости
|
|
(16.33) |
и для средней квадратичной скорости молекул
|
|
(16.34) |
Формула (16.34) для средней квадратичной скорости может быть также получена на основании формулы, описывающей среднюю кинетическую энергию поступательного движения молекул газа (см. лекцию №12).
Полученные
значения скоростей численно отличаются
друг от друга на величину, меньшую, чем
их значения, причем
![]() ,
что проиллюстрировано на рис. 16.4.
,
что проиллюстрировано на рис. 16.4.
Кроме
функции распределения по абсолютным
значениям скорости
![]() применяется
функцияраспределения
по значениям кинетической энергии
поступательного
движения молекул
применяется
функцияраспределения
по значениям кинетической энергии
поступательного
движения молекул
![]() ,
характеризующая вероятность попадания
значений кинетической энергии
,
характеризующая вероятность попадания
значений кинетической энергии![]() в
интервал
в
интервал![]() :
:
|
|
(16.35) |
Эти распределения справедливы только для равновесного состояния термодинамической системы. Вследствие достаточно общего метода их получения, они применимы не только для газов, но и для любых систем, движение микрочастиц которых описывается уравнениями классической механики.

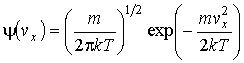 ,
,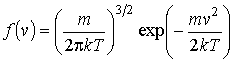
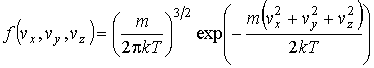 .
.
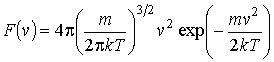
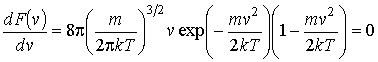 .
.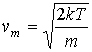 ,
,
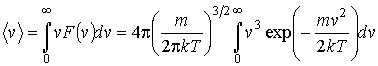
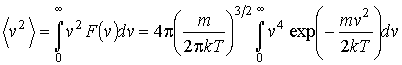 .
.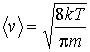
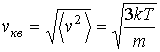 .
.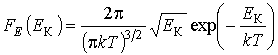 .
.