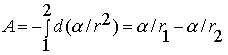Лекция №6 Механика Энергия

(Понятие о энергии. Два вида механической энергии. Работа. Мощность. Потенциальное поле сил. Потенциальная энергия)

6.1. Понятие о энергии. Два вида механической энергии

Опыт показывает, что различные формы движения материи способны к взаимным превращениям. Механическая форма движения способна превращаться в тепловую форму, тепловая форма превращаться в электрическую, электрическая – в магнитную, магнитная – в механическую и т.д. и т.п. Опытом установлено, что все взаимные превращения различных форм движения материи происходят в строго определенных количественных соотношениях. «Исчезновение» одной формы движения всегда сопровождается «возникновением» эквивалентного количества другой формы движения материи. Изучение закономерностей этих превращений привело к выводу, что должна существовать единая мера различных форм движения материи отражающая превращение одних форм движения материи в другие формы движения. Такой мерой является Энергия.

Состояния тел или системы тел и частиц описываются параметрами состояния в механике это: x,y,z, V_x,V_yV_z (координаты и скорость), в термодинамике V,p,T (объем, давление, температура), электродинамике Е_х , Е_y, Е_z, B_x, B_y, B_z. (электрическое и магнитное поле).

Энергия (в широком смысле) это единая мера превращения различных форм движения материи, являющаяся однозначной, непрерывной, конечной и дифференцируемой функцией параметров состояния системы.

Обычно изменения обусловленные различными формами движения рассматриваются раздельно поэтому и энергию так же удобно рассматривать как механическую, тепловую электромагнитную и т.д. В разделе механика мы будем иметь дело только с механической энергией, которая определяется параметрами состояния определяющими положение тела в пространстве r и определяющими быстроту изменения этого положения V

Эта механическая энергия может быть разбита на две части каждая из которых зависит только от одного параметра r или V . Часть механической энергии зависящей от положения тел в пространстве (от r ) получила название потенциальная энергия. Другая часть, зависящая от скорости движения, тел получила название кинетическая энергия.

4.2. Работа. Мощность.

Пусть частица под действием силы совершает перемещение по некоторой траектории 1-2 (рис. 6.1). В общем случае сила в процессе

Рис. 6.1. Определение работы силы

     движения частицы может изменяться как по модулю, так и по направлению. Рассмотрим, как показано на рис.5.1, элементарное перемещение , в пределах которого силу можно считать постоянной.

      Действие силы на перемещении характеризуют величиной, равной скалярному произведению , которую называют элементарной работой силы на перемещении . Ее можно представить и в другом виде:

     

,

     где - угол между векторами и - элементарный путь, проекция вектора на векторобозначена (рис. 6.1).

     Итак, элементарная работа силы на перемещении

     

.

(6.1)

     Величина - алгебраическая: в зависимости от угла между векторами силы и или от знака проекции вектора силы на вектор перемещения она может быть как положительной, так и отрицательной и, в частности, равной нулю, если т.е. . Единицей измерения работы в системе СИ служит Джоуль, сокращенное обозначение Дж.

     Суммируя (интегрируя) выражение (6.1) по всем элементарным участкам пути от точки 1 до точки 2, найдем работу силы на данном перемещении:

     

.

(6.2)

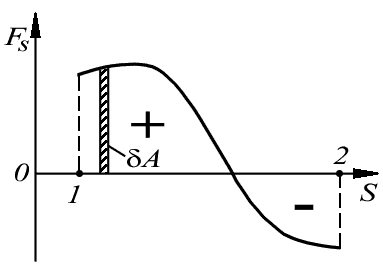
     Выражению (6.2) можно придать наглядный геометрический смысл. Изобразим график как функцию положения частицы на траектории. Пусть, например, этот график имеет вид, показанный на рис. 6.2. Из этого рисунка

Рис. 6.2. Графический смысл работы сил

     видно, что элементарная работа A численно равна площади заштрихованной полоски, а работа А на пути от точки 1 до точки 2 - площади фигуры, ограниченной кривой, ординатами 1 и 2 и осью s. При этом площадь фигуры над осью s берется со знаком плюс (она соответствует положительной работе), а площадь фигуры под осью s - со знаком минус (она соответствует отрицательной работе).

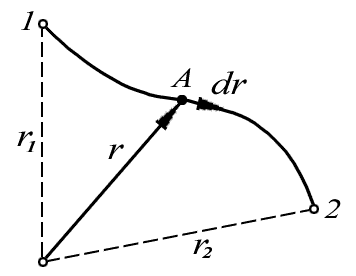
     Рассмотрим примеры на вычисление работы. Работа упругой силы где - радиус-вектор частицы А относительно точки О (рис. 6.3).

Рис. 6.3. Работа упругой силы

     Переместим частицу A, на которую действует эта сила, по произвольному пути из точки 1 в точку 2. Найдем сначала элементарную работу силы на элементарном перемещении :

     .

     Скалярное произведение где проекция вектора перемещения на вектор . Эта проекция равна приращению модуля вектора Поэтому и

     

     Теперь вычислим работу данной силы на всем пути, т. е. проинтегрируем последнее выражение от точки 1 до точки 2:

     

(6.3)

     Вычислим работу гравитационной (или аналогичной ей математически силы кулоновской) силы. Пусть в начале вектора (рис. 6.3) находится неподвижная точечная масса (точечный заряд). Определим работу гравитационной (кулоновской) силы при перемещении частицы А из точки 1 в точку 2 по произвольному пути. Сила, действующая на частицу А, может быть представлена так:

     

     где параметр для гравитационного взаимодействия равен , а для кулоновского взаимодействия его значение равно . Вычислим сначала элементарную работу этой силы на перемещении

     

     Как и в предыдущем случае, скалярное произведение поэтому

     

.

     Работа же этой силы на всем пути от точки 1 до точки 2

     

(6.4)

     Рассмотрим теперь работу однородной силы тяжести . Запишем эту силу в виде где орт вертикальной оси z с положительным направлением обозначен (рис.6.4). Элементарная работа силы тяжести на перемещении

     

Рис. 6.4. Работа однородной силы тяжести

     Скалярное произведение гдепроекция на орт равная - приращению координаты z. Поэтому выражение для работы приобретает вид

     

     Работа же данной силы на всем пути от точки 1 до точки 2

     

(6.5)

     Рассмотренные силы интересны в том отношении, что их работа, как видно из формул (6.3) - (6.5), не зависит от формы пути между точками 1 и 2, а зависит только от положения этих точек. Эта весьма важная особенность данных сил присуща, однако, не всем силам. Например, сила трения этим свойством не обладает: работа этой силы зависит не только от положения начальной и конечной точек, но и от формы пути между ними.

     До сих пор речь шла о работе одной силы. Если же на частицу в процессе движения действуют несколько сил, результирующая которых то нетрудно показать, что работа результирующей силы на некотором перемещении равна алгебраической сумме работ, совершаемых каждой из сил в отдельности на том же перемещении. Действительно,

     

(6.6)

     Введем в рассмотрение новую величину - мощность. Она используется для характеристики скорости, с которой совершается работа. Мощность, по определению, - это работа, совершаемая силой за единицу времени. Если за промежуток времени сила совершает работу , то мощность, развиваемая этой силой в данный момент времени, есть Учитывая, что , получим

     

.

(6.7)

     Единица мощности в системе СИ - Ватт, сокращенное обозначение Вт.

     Таким образом, мощность, развиваемая силой , равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения данной силы. Как и работа, мощность - величина алгебраическая.

     Зная мощность силы , можно найти и работу, которую совершает эта сила за промежуток времени t. В самом деле, представив подынтегральное выражение в (6.2) в виде получим

     

.

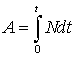     Следует также обратить внимание на одно весьма существенное обстоятельство. Когда говорят о работе (или мощности), то необходимо в каждом конкретном случае четко указывать или представлять себе, работа какой именно силы (или сил) имеется в виду. В ином случае, как правило, неизбежны недоразумения.