01-09-2014_14-57-50 / Моделир. Оптим.(з)_Подобие_ЛП_лекц

171

Равенство (7.13) принято называть соотношением двойственности, условия (7.14), (7.15)— условиями дополняющей нежесткости.

Теорема 7.4 (теорема двойственности). Прямая задача (7.11) имеет решение в том и только том случае, если двойственная задача (7.12) имеет решение; при этом значения данных задач совпадают, т. е. для любых их решений х* и у* выполнено соотношение двойственности (7.12).

При практическом применении теории двойственности особенно полезным является следующее утверждение, непосредственно вытекающее из теорем

7.3 и 7.4.

Теорема 7.5 (о дополняющей нежесткости). Точки x* Х и у* Y являются решениями взаимодвойственных задач (7.11) и (7.12) соответственно в том и только том случае, если выполняются условия (7.14), (7.15).

Итак, взаимодвойственые задачи ЛП имеют или не имеют решения одновременно. Следующая теорема показывает, что уже по их допустимым множествам можно отличить первый случай от второго.

Теорема 7.6. Если допустимые множества взаимодвойственных задач (7.11) и (7.12) непусты, то обе они имеют решение. Если же только у одной из них допустимое множество непусто, то ее значение бесконечно, т. е.

если X 0,Y 0, то sup <c,x>= ; x

если X 0, Y 0, то inf <b,y>=- . Y

Пример 7.2. Построить задачу двойственную к следующей задаче ЛП.

17х1 – 5 х2 + х3+ х4 – 8х5 max

3х1 – х2 – х3 + 4х4 + 7х5 ≤11

х1 – 5 х2 – 7х3 + х4 + 2х5 ≥-8

х1 + х2 + х3 + 3х4 – х5=4

х1≥0, х4≥0.

Решение. Составим таблицу перехода к двойственной задаче (табл. 7.1).

171

172

3y1 – y2 + y3 ≥17

–y1 + 5y2 + y3 = –5

–y1 + 7y2 + y3 =1 4y1 – y2 + 3y3 ≥1 7y1 – 2y2 – y3= –8

6.2.Симплексный метод

6.2.1. Геометрическая интерпретация симплексного метода

Выше рассмотрены основные теоремы линейного программирования, из которых следует, что если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений. Там же был указан путь решения любой задачи линейного программирования: перебрать конечное число допустимых базисных решений системы ограничений и выбрать среди них то, на котором функция цели принимает оптимальное решение. Геометрически это соответствует перебору всех угловых точек многогранника решений. Такой перебор, в конце концов, приведет к оптимальному решению (если оно существует), однако его практическое осуществление связано с огромными трудностями, так как для реальных задач число допустимых базисных решений хотя и конечно, но может быть чрезвычайно велико.

Число перебираемых допустимых базисных решений можно сократить, если производить перебор не беспорядочно, а с учетом изменений линейной функции, т. е. добиваясь того, чтобы каждое следующее решение было «лучше» (или, по крайней мере, не хуже), чем предыдущее, по значениям линейной

172

173

Такой перебор позволяет сократить число шагов при отыскании оптимума. Поясним это на графическом примере.

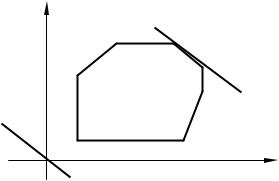
Пусть область допустимых решений изображается многоугольником ABCDEGH (рис. 6.12). Предположим, что его угловая точка А соответствует исходному допустимому базисному решению. При беспорядочном переборе пришлось бы испытать семь допустимых базисных решений, соответствующих семи угловым точкам многоугольника. Однако из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем к оптимальной точке С. Вместо семи перебрали только три вершины, последовательно улучшая линейную функцию.

Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программированиясимплексного метода (лат. simplex – простой, простейший выпуклый многогранник в n-мерном пространстве с n+1 вершиной, например, тетраэдр в 3-мерном пространстве).

Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере, не худшее) значение (по отношению к цели задачи) до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).

0

x1

Рис. 6.12. Область допустимых решений

Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г., однако, еще в 1939 г. идеи метода были разработаны российским ученым Л. В. Канторовичем.

Симплексный метод, позволяющий решить любую задачу линейного программирования, универсален. В настоящее время он используется для компьютерных расчетов, однако несложные примеры с применением симплексного метода можно решать и вручную.

173

174

Для реализации симплексного метода – последовательного улучшения решения – необходимо освоить три основных элемента:

способ определения какого-либо первоначально допустимого базисного решения задачи;

правило перехода к лучшему (точнее не худшему) решению;

критерий проверки оптимальности найденного решения.

Для использования симплексного метода задача линейного программиро-

вания должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений.

6.2.2. Симплексные таблицы

Пусть задача линейного программирования записана в каноническом виде в векторной записи

Считаем, что матрица А размера m×n, m < n, имеет ранг, равный m. Тогда система уравнений (6.17) совместна и имеет бесчисленное множество решений.

Из курса линейной алгебры известна процедура получения общего решения системы (6.17) методом последовательных исключений Жордана – Гаусса.

Выберем какой-нибудь базисный минор (т.е. минор порядка m, отличный от нуля) матрицы А. Для определенности будем считать, что он соответствует первым m столбцам матрицы А. Назовем переменные x1, …, xm − базисными, а остальные переменные xm+1, …, xn − свободными. При выборе базисных переменных на первом шаге достаточно воспользоваться следующим правилом: в качестве базисных переменных следует выбрать (если возможно) такие m переменных, каждая из которых входит только в одно из m уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.

Выполним элементарные преобразования строк расширенной матрицы системы (А/b) так, чтобы в первых m столбцах располагалась единичная матрица. В результате получим следующую систему уравнений, эквивалентную исходной:

Тогда общее решение системы уравнений (6.17) запишется следующим образом:

j m 1

174

175

где свободные переменные xm 1 ,..., xn могут принимать произвольные значения. Положив их равными нулю, получим частное решение:

или

которое называется базисным решением этой системы.

Если все компоненты базисного решения (6.21) удовлетворяют условию

стимым базисным решением системы (6.17) или угловой точкой допустимо-

го множества Е задачи линейного программирования (6.16)…(6.18). Если среди

зисное решение называется вырожденным (вырожденной угловой точкой), а соответствующая задача линейного программирования также называется вырожденной, а в противном случае ( bi0 0 ) – невырожденной.

В основе симплекс – метода лежит следующий факт:

Если задача линейного программирования (6.16)…(6.18) разрешима, то минимум целевой функции f(x) из (6.16) достигается хотя бы в одной из угловых точек допустимого множества X этой задачи.

Каждому выбору m базисных переменных системы (6.17) соответствует свое базисное решение. Поэтому число базисных решений (угловых точек) рав-

но числу всевозможных базисных миноров матрицы А, т.е. не превосходит C m . n

Предположим что задача линейного программирования (6.16)…(6.18) является невырожденной, а базисное решение (6.21) – допустимым.

Выразим целевую функцию задачи (6.16)…(6.17) через свободные переменные решения (6.21). Для этого подставим выражения базисных переменных через свободные из (6.20) в равенство (6.16):

Величина pj называется относительной оценкой небазисных перемен-

ных (xm+1,…, xn). Если pj < 0, то можно добиться уменьшения значения целевой функции f, вводя переменную xn в базис.

Для получения промежуточного допустимого базисного решения сим- плекс–метод превращает одну из базисных переменных в небазисную и вводит одну из небазисных переменных в базис. Необходимо выбрать базисную и небазисную переменные так, чтобы замена одной из них на другую давала максимальное приращение целевой функции.

175

176

В любом базисном решении базисные переменные положительны, а небазисные равны нулю. Следовательно, превращение небазисной переменной в базисную приводит к увеличению еѐ значения от нуля до некоторой положительной величины. Вводимая в базис переменная должна давать улучшение значения f. Для выбора вводимой в базис переменной следует присвоить небазисной переменной значение, равное единице, и вычислить изменение целевой функции.

имеет канонический вид, соответствующий допустимому базисному решению

Строке с номером i таблицы 6.3 соответствует i-ое уравнение системы

Пример 6.11. Записать одну из симплекс-таблиц для задачи:

x1 , x2 0.

176

177

Для того чтобы перейти к каноническому виду рассматриваемой задачи, прибавим к левым частям соответствующих ограничений-неравенств дополни-

В качестве базисных переменных удобно выбрать x3, x4 и x5, тогда переменные x1 и x2 будут свободными. Выпишем общее решение системы уравне-

ний из (6.26):

Полагая свободные переменные x1 и x2 равными нулю, получаем базисное решение x0 = (0;0;7;8;3). Очевидно, оно является допустимым базисным решением или угловой точкой множества X. Так как целевая функция задачи (6.26) зависит лишь от свободных переменных, то выражения (6.26) представляют собой канонический вид задачи линейного программирования, соответствующий допустимому базисному решению x0. Таким образом, искомая симплекстаблица имеет вид (табл. 6.4):

Таблица 6.4

Симплекс-таблица задачи 6.9

6.2.3. Описание симплекс-метода

Из анализа коэффициентов в условиях задачи (6.23)…(6.25) (или в соответствующей симплекс-таблице) можно сделать одно из следующих трех утверждений:

177

178

шения.

Замечание. Ситуация, описанная в теореме 6.8 возможна, если допустимое множество X задачи не ограничено.

ли хотя бы один из коэффициентов pj, j ≠ 0 в (6.23), например, pk, отрицателен (pk< 0) и при этом среди коэффициентов αik есть хотя бы один положительный, то существует допустимое базисное решение x1≠x0 множества Е, для которого

ными нулю, получим решение (6.27), (6.28) системы уравнений (6.24). По усло-

вию теоремы среди коэффициентов α есть положительные, поэтому с увели-

ik

чением xk может произойти нарушение условий неотрицательности (6.25) для

которая раньше всех обратиться в нуль при возрастании xk . С учетом (6.28) номер q находится из условия

178

(6.31)

Очевидно, что х1 является допустимым базисным решением системы (6.24); оно соответствует базисным переменным x1 ,..., xq 1 , xk , xq 1 ,..., xm . От-

метим, что в этом решении переменные хq и хk поменялись ролями: хq из базисных переменных перешла в свободные, а хk – наоборот.

Значение целевой функции (6.23) в точке x1 из (6.30) равно

Результаты теорем 6.7 … 6.9 лежат в основе симплекс-метода решения задач линейного программирования. Идея этого метода состоит в следующем.

Если в точке x0 из (6.21) выполняются условия теоремы 6.7 или 6.8, то решение задачи (6.16)…(6.18) на этом завершается.

Если же для точки x0 выполнены условия теоремы 6.9, то совершается переход от x0 к новому допустимому базисному решению x1 из (6.30), для которого f(x) уменьшается. Затем в точке x1 анализ коэффициентов задачи повторяется, и на основании теорем 6.7…6.9 делается одно из трех возможных заключений и т.д.

Так как число допустимых базисных решений задачи (6.16)…(6.18) не

конечное число раз. Поэтому в результате конечного числа шагов перехода к новому допустимому базисному решению задача будет решена или будет установлена ее неразрешимость.

Таким образом, симплекс – метод представляет собой направленный перебор допустимых базисных решений (угловых точек допустимого множества) задачи линейного программирования с последовательным уменьшением целевой функции.

179

180

Найдем канонический вид задачи, соответствующий допустимому базисному решению x1 из (6.30). Считая свободными переменные

(6.32)

Выразим из равенства (6.32) переменную xk и подставим найденные вы-

ражения в остальные уравнения системы (6.24) и в формулу (6.23) для целевой функции. В результате получим:

Зависимость целевой функции от новых свободных переменных примет

вид:

(6.34)

Задача линейного программирования (6.32) … (6.34) имеет канонический вид, соответствующий допустимому базисному решению x1 из (6.30)…(6.31) и может быть записана с помощью симплекс – таблицы. Компоненты нового базисного решения x1 можно найти, приравняв нулю свободные переменные

x j , j (m 1) : n, j k и хq и найдя при этом условии значения базисных пе-

ременных из (6.32), (6.33).

По знакам коэффициентов в системе (6.32), (6.33) и в выражении для целевой функции (6.34) можно сделать одно из трех приведенных выше заключе-

Как указано выше реализация симплекс – метода значительно упрощается при использовании симплекс - таблиц. Записав коэффициенты уравнений (6.19) и целевой функции (6.22) соответствующим образом (см. табл. 6.5), получим симплекс – таблицу задачи для угловой точки x0 из (6.21). Здесь введен

180