01-09-2014_14-57-50 / Моделир. Оптим.(з)_Подобие_ЛП_лекц

131

Простейшими примерами выпуклых функций одной переменной служат парабола y=x2 и экспонента y=ex. Функции y=-x2 и y=-ex являются вогнутыми.

Если при всех x1, x2 X x1 x2 и [0,1] неравенство (3.1) выполняется как строгое ( ), то f называется строго выпуклой на X (рис 3.7,а). Функция называется (строго) выгнутой, если - f (строго) выпукла (рис. 3.7, б).

Рис.3.7. Строго выпуклая (а) и строго вогнутая функции, их производные (пунктир) и функция, имеющая линейный участок

Функция f(x), определенная на выпуклом множестве Х, называется сильно выпуклой с константой l > 0, если

графику функции y=f(x) от точки B= (x2, f(x2)) до точки А= (х1, f(x1)) (рис.3.8).

Рис.3.8. График сильно выпуклой функции.

Уравнения

131

132

в плоскости xOy описывают прямую L (секущую), соединяющую точки А и В, а уравнения

точки А и В. Неравенство (3.2) в этом случае означает, что график функции y = f(x) на плоскости хОу расположен ниже не только секущей, соединяющей точки А и В, но и параболы Р, прогиб которой определяется параметром l и его можно выбрать сколь угодно малым. Другими словами, в области, ограниченной секущей и графиком функции, можно построить параболу, соединяющую точки А и В.

Теорема3.1 Непрерывно дифференцируемая на выпуклом множестве X функция f выпукла на этом множестве тогда и только тогда, когда для любых x1,x2 X верно неравенство

получаемое из разложения функции f(x) в ряд Тейлора в точке x1 путем исключения членов второго и более высокого порядка разложения

где h достаточно малое число, h . Известно, что если функция f дифференцируема в точке x1, то она в этой точке непрерывна и

f(x1) = ( f/ x1, f/ x2,.., f/ xn)т,

т.е. представляет собой вектор частичных производных первого порядка, вычисленных в точке x1 и называется градиентом функции f в точке x1.

Теорема 3.2 Пусть функция f дважды непрерывно дифференцируема на выпуклом множестве X, содержащем хотя бы одну внутреннюю точку, и2f(x)- ее гессиан. Тогда для выпуклости f на множестве X необходимо и достаточно, чтобы матрица 2f(x) была неотрицательно определена при всех x X, т.е. чтобы неравенство

132

133

выполнялось для всех точек x X, h En. Здесь числовая матрица 2f(x) называется гессианом (или матрицей Гессе). Если функция f имеет непрерывные частные производные второго порядка (дважды непрерывно дифференцируема ) в точке x1, то она дважды дифференцируема в x1 и обладает матрицей Гессе вида

Аналогичные утверждения имеют место и для вогнутых функций. При этом в формулах (3.2) и (3.4) знак неравенства следует заменить на .

Проверка функции на выпуклость.

Функция f выпуклая, если ее матрица Гессе положительно определена ( 0 ) или положительна полуопределена для всех значений x1,x2,..,xn.

Проверка функции на выгнутость.

Функция f выгнутая, если ее матрица Гессе отрицательно полуопределена ( 0 ) для всех значений x1,x2,..,xn.

Строго выпуклая или вогнутая функция имеет единственный экстремум, являющийся соответственно глобальным минимумом или максимумом. Функция, имеющая линейный участок (рис 3.7, в), имеет бесконечное число экстремумов, равных по величине.

Для суждения об одноэкстремальности при наличии ограничений можно воспользоваться понятием выпуклости допустимого множества. Множество является выпуклым, если любой отрезок прямой, соединяющей две точки границ множества, целиком лежит внутри множества.

О выпуклости или вогнутости целевой функции можно судить также по характеру изменения ее частных производных f/ x. В случае строго выпуклой функции эта производная по мере увеличения аргумента возрастает (рис 3.7 а), а для строго выпуклой падает (рис 3.7 б). При наличии линейного участка целевой функции указанная производная на этом участке постоянна.

133

134

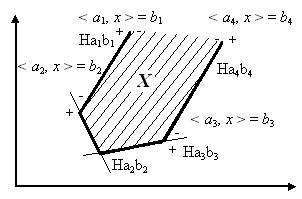
Выпуклое множество вида

X={x En} Ax b}={x En ai ,x> bi, i=1,..,m}

где A- некоторая матрица размера m*n со строками a1,..,am, b=(b1,..,bm) En(m=1,2,..). Принято называть полиэдральными или просто полиэдрами. Таким образом, полиэдр - это множество решений некоторой системы конечного числа линейных неравенств, или, что то же самое, пересечение конечного числа полупространств (рис. 3.9).

Рис.3.9. Полиэдральное множество (полиэдр).

Замечания 3.1.

1.Функцию f(x) называют выпуклой, если она целиком лежит не выше отрезка, соединяющего две ее произвольные точки. Функцию называют строго выпуклой, если она целиком лежит ниже отрезка, соединяющего две ее произвольные, но не совпадающие точки.

2.Если функция сильно выпуклая, то она одновременно строго выпуклая и выпуклая. Если функция строго выпуклая, то она одновременно выпуклая.

3.Выпуклость функции можно определить по матрице Гессе:

Если H(x) 0 x Rn, то функция выпуклая;

Если H(x) > 0 x Rn, то функция строго выпуклая;

Если H(x) lE x Rn, где Е- единичная матрица, то функция сильно выпуклая.

Отметим важное свойство выпуклой функции. Если функция f выпукла на множестве X, то для любых точек x1, x2,..., xm X и произвольных неотрицательных чисел 1+ 2+... m=1 имеет место неравенство Иен Сена

f( 1x1 + 2x2 +...+ mxm) 1f(x1) + 2f(x2) +...+ mf(xm).

При m=2 это неравенство совпадает с неравенством (3.1) из определения выпуклой функции.

134

135

Глава 4. Математические модели оптимизации

4.1 Постановка задачи оптимизации

Сама по себе постановка задачи оптимизации проста и естественна: заданы множество Х и функция (x),определѐнная на х, требуется найти точки минимума или максимума функции на х. Задачу на минимум запишем в виде:

При этом будем называть целевой функцией, х - допустимым множеством, любой элемент х Х – допустимой точкой задачи (4.1). Если х совпадает

Ограничения подразделения: а) на линейные (I, II) и нелинейные (III, IV) (рис.4.1);

б) детерменированные (А, В) и стахостатические (группы кривых Сj) (рис.4.2).

Стохастические ограничения являются всевозможными, вероятными, случайными.

Необходимо подчеркнуть, что само понятие точки минимума, т.е. решения задачи (4.1), неоднозначно и требует уточнения.

Точка х* Х называется:

1) точкой глобального минимума функции на множестве Х или глобаль-

135

136

2) точкой локального минимума на Х или локальным решением задачи

минимумов для произвольной кривой (x).

Задача оптимизации, в которой критерий оптимальности (x) имеет в области Х единственный локальный минимум, называется одноэкстремальной

(унимодальной) задачей оптимизации. Простейшими из унимодальных функ-

ций являются выпуклые функции (рис. 4.4.а).

На рис.4.4 приведены примеры унимодальных одномерных функций. Задача оптимизации, в которой критерий оптимальности (х) имеет не-

сколько локальных минимумов, называется многоэкстремальной задачей оп-

тимизации.

Обычные методы решений много экстремальных задач обеспечивают нахождение лишь отдельной особой точки, в которой частная производнаяf x 0 . Такой точкой в зависимости от случайных обстоятельств (выбор

начального приближения) может быть любой из локальных минимумов или точка перегиба. В связи с этим существенное значение имеет исследование

136

137

условий, при которых решение обеспечивает нахождение глобального минимума.

Если неравенство в (4.2) или (4.3) выполняется как строгое при х х*, то говорят, что х* -точка строгого минимума (строгое решение) в глобальном или локальном смысле. Ясно, что глобальное решение является и локальным; обратное неверно.

Для отражения того факта, что точка х* Х является точкой глобального минимума функции на Х, будем использовать запись:

мальное значение функции на Х. Множество всех точек глобального минимума на Х обозначим через

мизации или наоборот. Это объясняется тем, что минимум функции равен максимуму функции – , взятому с противоположным знаком, и достигаются оба эти экстремума при одних и тех же значениях переменных (рис.4.5). В точ-

ке х* min (x*)= -max(- (x*)) .

y= (x)

} min (x)

0 max (x){ x*. х

симизации, то достаточно вместо f (x1 , x2 ,..., xn ) взять в качестве целевой функ-

тивоположный. Полученное значение будет оптимумом исходной задачи. По анологии с (4.1) будем записывать задачу максимизации функции на множе-

137

138

(4.4)

Решения задач (4.1) и (4.4), т.е. точки минимума и максимума функции на Х называют также точками экстремума, а сами задачи (4.1) и (4.4)-

экстремальными задачами.

4.2 Условия оптимальности.

При изучении любого типа задач оптимизации важное место занимает во-

прос об условиях оптимальности или, как говорят, условиях экстремума.

Различают необходимое условие оптимальности, т.е. условия которым должна удовлетворять точка, являющаяся решением задачи, и достаточные условия оптимальности, т.е. условия из которых следует, что данная точка является решением задачи.

Замечания:

1.Если функция обладает свойством унимодальности, то локальный минимум автоматически является глобальным минимумом.

2.Если функция не является унимодальной, то возможно наличие нескольких локальных оптимумов, при этом глобальный минимум можно определить путѐм нахождения всех локальных оптимумов и выборе наименьшего из них.

Теорема 4.1.(необходимое условие минимума первого порядка): Пусть

Точка х*, удовлетворяющая условию (4.5), называется стационарной точкой функции или задачи (4.1). Ясно, что стационарная точка не обязана быть решением, т.е. (4.5)не является достаточным условием оптимальности. Такие точки являются подозрительными на оптимальные.

Пример 4.1. Рассмотрим, например, функцию f (x) x3 (рис.4.4). Эта функция удовлетворяет необходимому условию оптимальности, однако, не

онарная точка.

Если стационарная точка не соответствует локальному опт муму (миниму-

138

139

му или максимуму), то она является точкой перегиба или седловой точкой. Для того, чтобы провести различия между случаями, когда стационарная точка соответствует локальному минимуму, локальному максимуму или является точкой перегиба, необходимо построить достаточные условия оптимальности.

x* x

Рис.4.6. График функции, имеющей точку перегиба.

Теорема 4.2.(необходимое условие минимума второго порядка): Пусть функция дважды дифференцируема в точке x* E n . Если х* - локальное решение задачи (4.1), то матрица неотрицательно определена, т.е.

Достаточное условие локальной оптимальности содержит характерное

Теорема 4.3. (достаточное условие минимума второго порядка): Пусть функция дважды дифференцируема в точке x* E n . Предположим, что

Тогда х*- строгое локальное решение задачи (4.1). Для функции числового

как скалярная величина не отрицательна и положительна соответственно.

139

140

Итак, для функции числового аргумента не является гарантией наличие

статочным условием является следующая теорема.

Теорема 4.4. Пусть в точке х* первые (n-1) производные функции обращаются в нуль, а производная n-го порядка отлична от нуля:

1)Если n-чѐтное, то х* - точка перегиба;

2)Если n-нечѐтное, то х*- точка локального оптиума. Кроме того:

а) если эта производная положительная, то х*- точка локального миниму-

ма;

б) если эта производная отрицательна, то х* - точка локального максиму-

4.1) , вычислим:

Так как порядок первой отличной от нуля производной равен 3 (нечѐтное число), точка х=0 является точкой перегиба.

Пример 4.2. Рассмотрим функцию:

определенную на всей действительной оси.

dfdx 30x5 180x4 330x3 180x2 30x2 (x 1)(x 2)(x 3) .

Ясно, что первая производная обращается в нуль в точках х=0,1,2,3, и, следовательно, эти точки можно классифицировать как стационарные.

Вычислим значения второй производной в четырѐх точках х=0,1,2,3 (табл.4.1)

Значения второй производной функции (табл. 4.1).

140