Иваненко Гидравлика

Лекция 7

Гидродинамика. Виды движения жидкости

Гидродинамика – раздел гидравлики (механики жидкости), в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Причинами, вызывающими движение жидкости, являются действующие на нее силы: сила тяжести, внешнее давление и т. п. Основными параметрами, характеризующими движение, являются внутреннее давление и скорость в отдельных точках. Давление называется гидродинамическим. В общем случае скорость и давление являются функциями координаты и времени. Задача гидродинамики состоит в изучении взаимодействия между скоростью и давлением в отдельных точках.

Гидростатическое давление в каждой точке жидкости, как уже известно, является функцией только координат x, y, z, гидродинамическоежедавлениеР,крометого,можетизменятьсяисовременемt, являясь функцией времени, Р = f (x, y, z, t).

Скоростью течения жидкости u в заданной точке называется скорость перемещения данной частицы жидкости в пространстве. Скорость течения зависит от положения точек (координат x, y, z)

иможет изменяться со временем t, т. е. u = f (x, y, z, t).

Взависимости от изменения во времени основных элементов движения – давления и скорости, различают следующие виды движения жидкости:

• неустановившееся движение, при котором скорость и дав-

ление в каждой точке потока изменяются с течением времени, т. е.

Р = f1 (x, y, z, t) и u = f2 (x, y, z, t).

Например, движение в реке при изменяющемся горизонте воды;

• установившееся движение – это движение, при котором давление и скорость в каждой точке потока не изменяются с течением времени и зависят только от координат точки, т. е.

Р = f1 (x, y, z) и u = f2 (x, y, z) или dp/dt = 0, du/dt = 0.

Например, движение в канале при постоянном горизонте воды. Установившееся движение может быть равномерным и неравно-

мерным.

Равномерное движение – когда элементы движения (скорость, глубина, давление и т. д.) не меняются вдоль потока. Например, движение жидкости по трубам с постоянной скоростью.

Неравномерное движение – когда элементы движения (скорость, глубина, давление и т. д.) в каждой точке потока изменяются по длине. Например, движение в конической трубе, в которой по длине меняются поперечные сечения потока.

В зависимости от причин, вида сил и общих условий движения различают напорное и безнапорное движения.

Напорным называют движение, при котором жидкость заполняет все поперечное сечение трубопровода. Это движение осуществляется под действием внешних сил или под действием приложенного давления, превышающего атмосферное и сообщенного каким-либо внешним источником.

Безнапорное движение осуществляется самотеком, происходит под действием силы тяжести, жидкость не заполняет все поперечное сечение трубопровода и характеризуется наличием свободной поверхности с известным давлением на поверхности, обычно атмосферным.

Для описания движения частицы, а через нее и жидкости, существуют два метода: Лагранжа и Эйлера.

1. Метод Лагранжа. Для описания движения жидкости требуется описать движение каждой частицы. Описание движения жидкости методом Лагранжа сводится к рассмотрению положения частиц жидкости в любой момент времени.

Пусть в начальный момент времени t0 каждая частица имеет соответствующие начальные координаты x0, y0, z0. Однако к моменту t для каждой частицы координаты изменятся. Движение можно считать описанным (определенным), считает Лагранж, если возможно указать для каждой частицы координаты x, y, z в произвольный мо-

мент времени t как непрерывные функции от начальных координат

x0, y0, z0, т. е.

x = f1(x0, y0, z0, t), y =f2 (x0, y0, z0, t),

z = f3(x0, y0, z0, t),

где переменные x, y, z называют переменными Лагранжа.

Метод Лагранжа из-за громоздкости и трудности решения может использоваться при детальном изучении поведения лишь отдельных частиц жидкости. Использование этого метода для инженерных расчетов затруднительно.

2.МетодЭйлера.СутьметодаЭйлеразаключаетсявтом,чтоизучение движения жидкости подменяется изучением изменения поля скоростей. Под полем скоростей понимают некоторую достаточно большую совокупность точек бесконечного пространства, занятого движущейся жидкостью, когда в каждой точке пространства в каждый момент времени находится частица жидкости с определенной скоростью (вектором скорости). Несмотря на то что исходные условия создания модели движущийся жидкости довольно сложные, тем не менее, метод Эйлера весьма удобен для расчетов.

Построениеполяскоростейосуществляетсяследующимобразом. В некоторый момент времени (например, t0) произвольным образом выберем необходимое число точек, в которых находятся частицы жидкости. Приписав их скорости точкам неподвижного пространства, сделаем «моментальную фотографию» поля скоростей на выбранный момент времени. В следующий момент времени в тех же выбранных точках неподвижного пространства будут находиться другие частицы жидкости, имеющие другие скорости u. Выполнив уже известную процедуру второй раз, получим новую «моментальную фотографию» поля скоростей на момент времени t1. Теперь вместо изучения траекторий частиц жидкости будем сравнивать поля скоростей.

Изменение этого поля описывается следующей системой: ux = f1 (x, y, z, t),

uy = f2 (x, y, z, t), uz = f3 (x, y, z, t).

Переменные ux, uy, uz – три взаимноперпендикулярные составляющие полной скорости – еще называют переменными Эйлера. Они позволяют определить скорость в любой точке пространства в любой момент времени.

Поле скоростей движения жидкости иногда называют гидродинамическим полем по аналогии с электромагнитным, тепловым и другими полями. Это определение не противоречит физической стороне процесса движения жидкости. Такое поле называют нестационарным (изменяющимся) гидродинамическим полем. В частном случае, когда во всех точках неподвижного пространства с течением времени предыдущие частицы жидкости сменяются другими с такими же скоростями, поле скоростей во времени не меняется.

Лекция 8

Основные элементы потока. Уравнение неразрывности для капельных

и упругих жидкостей

Основной кинематической характеристикой гидродинамического поля является линия тока.

Линия тока (рис. 20, а) – кривая, в каждой точке которой вектор скорости направлен по касательной к кривой. Это мгновенная характеристика потока. Часто путают понятия линия тока и траектория.

Траектория – это путь движущейся частицы в течение некоторого промежутка времени. При установившемся движении траектория движущейся частицы совпадает с линией тока.

Если в движущейся жидкости выделить весьма малую площадку dω1, через которую провести линии тока, то полученная поверхность называется поверхностью тока, а образованное этой поверхностью тело будет называться трубкой тока (рис. 20, б). Жидкость, наполняющая трубку тока, называется элементарной струйкой. Поскольку линии тока никогда не пересекаются, то поверхность трубки тока является непроницаемой внешней границей для элементарной струйки жидкости. Сечение трубки тока, нормальное к линиям тока, называется живым сечением элементарной струйки и dω2. При установившемся движении жидкости понятия линии тока и траектории движения частицы жидкости совпадают.

Рис. 20. Основные элементы потока: а – линия тока; б – линии тока (1) и трубка тока (2)

42

Элементарная струйка обладает следующими свойствами:

•форма элементарной струйки остается неизменной во времени;

•обмен частицами между отдельными струйками невозможен (вектор скорости направлен по касательной, нормальная составляющая равна 0);

•скорость и давление во всех точках сечения одинаковы в виду малых размеров сечения.

Совокупность элементарных струек, протекающих через достаточно большую, но ограниченных размеров площадь, называется потоком.

При изучении потока рассматривают плавно и резко изменяющееся движение. В дальнейшем будем рассматривать только плавно изменяющееся движение – это движение, близкое к параллельно струйчатому движению, имеющее определенные свойства:

•кривизна линии тока незначительна, т. е. радиус кривизны стремится к бесконечности;

•угол, образующий линии тока, близок к 0;

•поперечное сечение потока плоское и расположено по нормали

коси потока;

•давление в пределах сечения подчиняется законам гидростати-

ки.

Поток жидкости представляет собой совокупность элементарных струек жидкости. По этой причине основные кинематические характеристики потока во многом совпадают по своему смыслу с аналогичными характеристиками для элементарной струйки жидкости. Тем не менее, различия все же имеются. Так, в отличие от элементарной струйки, которая отделена от остальной жидкости поверхностью трубки тока, образованной линиями тока, поток жидкости имеет реальные границы в виде твердой, газообразной или жидкой сред. По типу границ потоки бывают:

•напорные, когда поток ограничен твердой средой по всему периметру сечения;

•безнапорные, когда часть сечения потока представляет собой свободную поверхность жидкости;

•гидравлические струи, когда поток ограничен только жидкой или газообразной средой. Если гидравлическая струя ограничена со всех сторон жидкостью, то она называется затопленной гидравлической струей, а если газовой средой, то такая струя называется незатопленной.

43

Основные элементы потока:

Живое сечение, ω (м²) – площадь поперечного сечения потока, перпендикулярная к направлению течения.

Смоченный периметр, χ (м) – часть периметра живого сечения, ограниченная твердыми стенками (рис. 21).

Рис. 21. Смоченный периметр выделен утолщенной линией

Гидравлический радиус R (м) – отношение площади живого сечения к смоченному периметру: R = ω/χ.

Например, для круглого сечения:

R = π · r2 / (2π · r) = r / 2 = d / 4.

Расход Q (м3/с, л/с и т. п.) – количество жидкости, проходящее через данное сечение в единицу времени.

Рассмотрим элементарную струйку, перемещающуюся с постоянной скоростью u = сonst. Объем жидкости, прошедший через живое сечение площадью dω на расстояние dS (рис. 22), составит: dW = dS · dω.

Рис. 22. Элементарная струйка

Разделив обе части на промежуток времени dt, за которое произошло перемещение, получим:

dW/dt = dS/(dt · dω), но dW/dt = dQ , а dS/dt = u, следовательно, dQ = u · dω, где u – средняя скорость элементарной струйки в рассматриваемом сечении для потока жидкости

где v – средняя скорость потока, м/с.

Уравнение неразрывности потока

Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 23 расходы во входном и выходном сечениях напорной трубы равны:

•так как проникновение жидкости через боковую поверхность невозможно (поверхность образована линиями тока);

•жидкость несжимаема;

•жидкость является сплошной средой (отсутствуют разрывы).

2

1

1

Q1 = Q2 = const 2

Рис. 23. Схема к уравнению неразрывности потока

При этих условиях можно записать:

Q1 = Q2 = сonst, с учетом (27) получим уравнение неразрывности потока:

Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и часто применяется в технике.

Рис. 24. Трубка Пито

Скорость жидкости в различных точках поперечного сечения неодинакова, поэтому для удобства расчетов введено понятие средней

скорости. Средняя скорость потока, v (м/с) – частное от деления расхода потока на площадь живого сечения: v = Q/ω. Измерение скорости потока и расхода жидкости производится с помощью специальных приборов: трубки Пито (рис. 24) и трубки Вентури.

Трубка Пито – изогнутая под углом 90° трубка, устанавливаемая отверстием наконечника по течению.

Лекция 9

Уравнение Бернулли. Смысл членов уравнения. Пьезометрическая и напорная линии, гидравлический уклон

Уравнение движения жидкости, устанавливающее связь между скоростью, гидравлическим давлением и вертикальной координатой для любой точки движущейся жидкости, носит название уравнения Бернулли. Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики.

Обычно уравнение Бернулли записывается для двух сечений элементарной струйки или потока и при установившемся движении жидкости имеет следующий вид:

а) для элементарной струйки идеальной жидкости (рис. 25):

б) для элементарной струйки реальной жидкости (рис. 26):

в) для потока реальной жидкости:

высота или скоростной напор, м; u – местная скорость элементарной струйки, м/c; v – средняя скорость потока, м/с; α – коэффициент

Кориолиса, или коэффициент кинетической энергии, учитывающий неравномерность распределения скоростей по живому сечению потока (для ламинарного режима течения в круглой трубе α = 2, для

турбулентного – α = 1,045–1,1); hw, ∑hw – суммарная потеря напора

при движении жидкости на рассматриваемом участке, м. Слагаемые, входящие в уравнение Бернулли, можно истолковать

с геометрической и энергетической точек зрения.

Например ∑hw – удельная механическая энергия, затрачиваемая на преодоление сопротивления движению жидкости между сечениями потока и переходящая в тепловую энергию, которая состоит из:

где ∑hдл – потери энергии (напора) на трение по длине; ∑hмест – местные потери энергии (напора).

Для определения геометрического смысла уравнения Бернулли рассмотрим элементарную струйку жидкости, движущейся относительно произвольно выбранной плоскости сравнения (см. рис. 25). Выберем три сечения: 1–1; 2–2; 3–3, центры тяжести которых от-

носительно плоскости сравнения 0–0 расположены на высотах z1; z2; z3. В центры тяжести выбранных сечений установим пьезометры и трубки Пито. Под действием давления жидкость в пьезометрах поднимается на высоту hp= Р/γ.

В трубках Пито под действием давления и скорости жидкость поднимается выше уровня в пьезометрах на высоту hи = и2/2g (см.

рис. 25).

Все члены в уравнении Бернулли представляют собой геометрические высоты и имеют размерность длины.

Так как сумма трех членов Р/γ, z и и2/2g для идеальной жидкости постоянна вдоль оси струйки, то уровни жидкости в трубках Пито, установленных в различных сечениях, будут всегда лежать в одной горизонтальной плоскости, называемой напорной плоскостью, т. е. напорная линия E–E (см. рис. 25) будет горизонтальна. В этом состоит геометрический смысл уравнения Бернулли для идеальной жидкости. Для идеальной жидкости линия Р–Р также будет горизонтальной.

Если плавной кривой соединим уровни жидкости в пьезометрах, то получим пьезометрическую линию P–P (см. рис. 25, 26), которая может подниматься или опускаться, но никогда не пересекается с напорной линией.

Сумма трех высот называется полным напором и обозначается Н, т. е. полный напор представляет собой сумму пьезометрического Нр = hp + z = Р/γ + z и скоростного hи = и2/2g напоров:

С энергетической точки зрения уравнение Бернулли выражает закон сохранения энергии. Полный напор Н – это полная удельная энергия жидкости в рассматриваемом сечении. Сумма трех членов есть сумма трех удельных энергий: удельной потенциальной энергии давления Р/γ, удельной потенциальной энергии положения z, удельной кинетической энергии и2/2g. Для идеальной жидкости сумма трех удельных энергий (полный напор) по длине струйки есть величина постоянная.

Реальная жидкость в отличие от идеальной обладает вязкостью. При движении реальной жидкости ее вязкость обусловливает сопротивление движению и вызывает потерю части энергии, поэтому полный напор уменьшается по длине струйки. Следовательно, уровни жидкости в трубках Пито будут снижаться по ходу движения (см.

рис. 26). Напорная линия Е–Е, проведенная по этим уровням для вязкой жидкости, будет наклонной, нисходящей. Разность между горизонтальными линиями Е–Е, проведенными на уровне жидкости в трубках Пито в сечениях 1–1 и 2–2, представляет собой потери напора hw на участке между этими сечениями.

Таким образом для реальной жидкости:

Н1 = Н2 + hw.

Потери напора, отнесенные к единице длины струйки, называются гидравлическим уклоном и обычно обозначаются буквой J:

где L – расстояние между сечениями 1–1 и 2–2.

Величина гидравлического уклона вдоль струйки может изменяться, так как зависит от потерь напора на различных участках.

Изменение пьезометрического напора, отнесенное к единице длины, называется пьезометрическим уклоном:

Пьезометрический уклон может быть направлен как в сторону движения, так и в сторону, противоположную движению.

При помощи уравнения Бернулли, как указывалось раньше, в гидравлике решается большое количество практических задач и выводится много расчетных формул. Для правильного применения необходимо иметь в виду следующие условия его применения:

1.Уравнение Бернулли выведено для плавно изменяющегося движения потока, а поэтому может применяться лишь к таким двум сечениям, вблизи которых поток удовлетворяет условиям «плавной изменяемости».

2.Сумму гидродинамического давления и высоты положения, т. е. двухчлен Нр =Р/γ + z, или пьезометрическую высоту, имеем право относить к любой точке каждого из двух взятых сечений, однако на практике ее удобно относить или к точкам на свободной поверхности потока, или к точкам, находящимся в центре тяжести сечений.

Вэтих случаях уравнение Бернулли приводится к сокращенному виду.

Лекция 10

Гидравлические сопротивления. Основное уравнение равномерного движения. Два режима движения жидкости.

Число Рейнольдса

Как указывалось в предыдущей лекции, при движении реальной жидкости происходит потеря напора или потеря энергии потока, выражением(мерой)которойявляютсягидравлическиесопротивления. Знаменитый русский ученый Д. И. Менделеев в своем сочинении «О сопротивлении жидкостей и о воздухоплавании» в 1880 г. указывал на существование в природе двух режимов движения жидкости с различными законами ее сопротивления. Эта же мысль была развита и доказана в 1883 г. русским физиком Н. П. Петровым (1836–1920), впервые установившим, что «при смазке силы трения, определяемые вязким сопротивлением при спокойном движении, пропорциональны первой степени скорости».

Полные потери напора можно представить как сумму всех видов потерь напора – местных потерь и потерь напора по длине (31). Оценка величины местных потерь напора или деформаций жидкости в потоке практически всегда базируется на результатах экспериментов, по которым определяются величины коэффициентов потерь. Для вычисления потерь напора по длине имеются более или менее надежные теоретические предпосылки, позволяющие вычислять потери с помощью привычных формул. Основной причиной таких сопротивлений являются силы трения.

Рассмотрим вначале потери напора, вызванные силами трения (потери по длине), а также их связь с основными параметрами потоков.

Установим закономерность между потерями напора и силами трения. Для этого выделим в трубе или открытом канале с движущейся жидкостью объем жидкости, ограниченный двумя попереч-

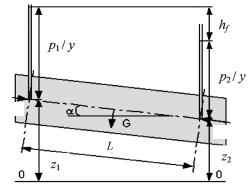
ными сечениями 1–1 и 2–2, находящимися на расстоянии L друг от друга (рис. 27).

При равномерном движении площади живых сечений, а следовательно, и скоростные напоры равны, поэтому hl = z1 + p1/γ – z2 – p2/γ.

Выделенный объем жидкости находится в равномерном движении. Равномерное движение возможно лишь в случае, когда все силы, действующие на тело, уравновешены. Рассмотрим все силы, которые действуют на выделенный объем жидкости.

На выделенный объем жидкости действуют:

1. Сила тяжести G = ρ · g · ω · L, приложенная в его центре тяжести.

2. Силы гидродинамического давления P1 = p1 · ω и P2 = p2 · ω , нормальные к сечениям и направленные в разные стороны.

3.Сила трения, возникающая на поверхности соприкосновения жидкости со стенками T = τ · χ · L , направленная противоположно движению.

4.Так как движение равномерное (без ускорения), силы инерции не возникают.

Спроецируем все действующие силы на ось направления движения жидкости:

P1 – P2 + G · sin α – T = 0,

p1 ·ω – p2 ·ω +ρ · g · ω · L · sin α – τ · χ · L = 0, L · sin α = z1 – z2,

ω (p1 – p2) + ρ · g · ω (z1 – z2) = τ · χ · L .

P1

P2

Рис. 27. Схема равномерного движения

52

Разделив на ρ · g · ω с учетом (3), получим

(p1 −γ p2 )+(z1 − z2 )= τγLωχ.

Левая часть выражения есть не что иное, как потери напора на рассматриваемом участке, т. е. можно записать

Выражение (35) является основным уравнением равномерного движения. Напряжение силы трения, отнесенное к единице веса, равно произведению гидравлического радиуса на гидравлический уклон.

При проведении многочисленных экспериментов с потоками движущейся жидкости было неоднократно подмечено, что на величину гидравлических сопротивлений, кроме физических свойств самой жидкости, формы и размеров каналов, состояния их стенок, существенное влияние оказывает особенности движения частиц жидкости в потоке. Впервые дал теоретическое обоснование этой зависимости английский физик Осборн Рейнольдс. Суть его эксперимента заключалась в следующем.

В емкость А (рис. 28) достаточного большого объема была вставлена длинная (не менее 20 диаметров) стеклянная трубка В. На конце этой трубки устанавливался кран С для регулирования расхода жидкости. Измерение расхода жидкости осуществлялось с помощью мерной емкости, расположенной в конце трубки. Из малого бачка D

спомощью тонкой изогнутой трубки по центру основной трубки вводилась подкрашенная жидкость. Ее расход также регулировался

спомощью краника Е. Уровень жидкости в основном баке А поддерживался постоянным. Плавно меняя расход жидкости в трубке, Рейнольдс отметил, что при малых скоростях движения жидкости подкрашенная струйка жидкости текла по центру потока жидкости, не смешиваясь с остальной жидкостью потока. Однако при определенной скорости жидкости подкрашенная струйка жидкости теряла свою устойчивость и, в конечном итоге, частицы окрашенной жидкости перемешивались с остальной жидкостью. При снижении ско-

53

Рис. 28. Схема установки Рейнольдса

рости движения жидкости положение восстанавливалось: хаотичное движение частиц жидкости снова становилось упорядоченным. Рейнольдс менял длину и диаметр трубки, вязкость жидкости, количество подкрашенных струек жидкости и установил, что эффект перемешивания (смена режима течения жидкости) зависит от скорости движения жидкости, ее вязкости и от диаметра трубки, причем при увеличении вязкости жидкости для смены режима течения жидкости требовалась большая скорость. Отсюда Рейнольдс сделал вывод, что смена режима движения жидкости зависит от целого комплекса параметров потока, а именно от соотношения, которое получило название числа Рейнольдса:

Число Рейнольдса оказалось безразмерной величиной, представлявшей собой отношение сил инерции к силам вязкостного трения.

Режимы движения всех потоков (напорных и безнапорных) можно разделить на два типа (рис. 29):

• ламинарный режим – спокойный, параллельноструйный (жидкость движется слоями без поперечного перемешивания), при ма-

Рис. 29. Шкала режимов

54

лых скоростях движения жидкости, причем пульсации скорости

идавления отсутствуют;

•турбулентный режим – бурлящий, вихреобразный, с водоворотами, при больших скоростях движения жидкости. При турбулентном режиме слоистость нарушается, движение жидкости сопровождается перемешиванием и пульсациями скорости и давления.

Для выяснения типа режима нужно рассчитать число Рeйнольдса Re и сравнить его с критическим числом Reкр. Критическое число Рeйнольдса Reкр – это число, при котором наступает смена режима движения. Его величина для напорных потоков Reкр = 2320, а для безнапорных потоков Reкр = 500.

Многочисленныеэкспериментальныеисследованиягидравлических сопротивлений показывают, что между ними и скоростью движения жидкости имеется зависимость hl = f(v). Важным оказалось то обстоятельство, что при смене режима движения существенно менялась зависимость величины гидравлических сопротивлений от скорости движения жидкости. При преобладании сил вязкости – режим ламинарный, при преобладании сил инерции – режим турбулентный. Этот факт можно проиллюстрировать на графике зависимости потерь напора от скорости, построенном в логарифмической системе координат (рис. 30). Если опытные данные нанести на график, то можно выявить три области: ламинарную (линия AB), турбулентную (линия CD) и неустойчивую, расположенную между точками B и C. Точки В и С называются критическими, т. е. точками, в которых происходит изменение режима, точка В – нижней критической точкой. Скорости, соответствующие этим точкам, называются критическими скоростями. Для точек В и С характерно то, что при скоростях меньше vн.к всегда наблюдается ламинарный режим, а при скоростях больших vв.к – турбулентный режим. При изменении скоростей от малых к большим ламинарный режим может удерживаться до точки Е. При изменении скоростей от больших к малым турбулентный режим может удерживаться до точки В. Значение числа Рейнольдса, соответствующее нижней критической точке В, называется нижним критическим числом Рейнольдса

иравно

Rен.к = vн.к · d/υ.

Число Рейнольдса в верхней критической точке С называется верхним критическим числом и равно:

55

D

C

E

Rев.к = vв.к · d/υ.

Потери напора по длине связаны со скоростью зависимостью, которая выражается уравнением

hl = а · vm,

где hl – потери напора по длине; a – коэффициент пропорциональности; v – средняя скорость потока; m – показатель степени.

Прологарифмировав данное уравнение, можно получить линей-

ную зависимость: lg hl = lg a + m · lg ν или m = lgh1 −lga . Если точlgv

ки, соответствующие значениям lg hl, lg v, нанести на график (рис. 31), то значение показателя степени m определится как тангенс угла наклона прямых в ламинарной и турбулентной областях к горизонтальной оси.

Для расчетов можно принять:

1. Для ламинарного участка наклон линии к оси абсцисс tg 45° = 1,2.

2.Для турбулентного участка наклон линии превышает единицу

иизменяется в пределах 1,75–2,0.

56

Лекция 11

Ламинарный и турбулентный режимы движения в круглой трубе

Рассмотрим характер распределения скоростей в сечении потока при ламинарном (от лат. lamina – слой) и турбулентном (от лат. turbulentus – беспорядочный) режимах движения жидкости.

Структура и свойства ламинарного потока

Как показали теоретический анализ и опыты, при ламинарном режиме движения жидкости в круглой трубе скорости в поперечном сечении распределены неравномерно по сечению, причем при движении существуют лишь продольные составляющие скоростей.

Чтобы установить картину изменения скорости по живому сечению, рассмотрим наиболее интересный и важный случай движения вязкой жидкости в напорном трубопроводе круглого сечения радиусом r (рис. 32). Совместим ось 0x с осью трубы и наметим ось r по направлению измерения диаметра. Выделим внутри трубы цилиндрический столб движущейся жидкости радиусом r (заштрихован).

Рис. 32. Схема для рассмотрения ламинарного потока

57