3. Третий уровень

1. [691] Напишите формулу бинома Ньютона (а+b)ⁿ для данного натурального n.

2. [692] Известно, что функция y=f(x) имеет единственный корень на отрезке [а; b]. Найдите этот корень методом половинного деле­ния с любой наперед заданной степенью точности.

3. [693] Постройте параболу y=x²+px+q, где р и q подобраны так, что график параболы пересекает оси координат в трех точках. Про­ведите окружность через эти три точки.

4. [694] Даны n точек на координатной плоскости. Проведите ок­ружность наименьшего радиуса, в которой содержатся все данные точки.

5. [695] Переведите запись числа из системы счисления с основа­нием р в систему счисления с основанием q, где р и q<=16.

6. [696] Решите систему n линейных уравнений с n неизвестными, используя метод последовательного исключения неизвестных, то есть метод Гаусса.

7. [697] Решите систему n линейных уравнении с n неизвестными, используя определители n-го порядка.

Тесты и результаты.

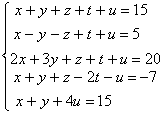
(1; 2,3; 4; 5).

8. [698] Треугольник задан сторонами а, b и с. Найдите его медиа­ны, биссектрисы, высоты, площадь и периметр.

9. [699] “Магический n-угольник". Правильный n-угольник называ­ется магическим, если в каждой его вершине и в каждой его стороне проставлены все натуральные числа от 1 до 2*n, и сумма чисел в вершине и прилежащих ей сторонах одинакова для каждой верши­ны. Для данного n распечатайте как можно больше магических n-угольников.

10. [700] Найдите наибольший общий делитель дробно - рациональ­ной функции, если корни числителя и знаменателя являются целы­ми числами. Сократите дробь, определяя коэффициенты нового числителя и знаменателя.

5. К о м б и н а т о р и к а.

6. 1. Первый уровень

1. [801] Найдите все расстановки одного белого, одного синего, од­ного красного и трех черных кружков в ряд.

2. [802] Найдите все расстановки одного знака плюс ("+"), одного знака минус ("-") и четырех звездочек ("*") в ряд.

3. [803] Даны k предметов с массами m1, m2,...mk. Выделите все группы предметов, у которых сумма масс равна S.

4. [804] Даны n чисел. Выделите из них группы, содержащие от 1 до n элементов, каждая из которых имеет данное произведение q. Одно число q считается имеющим произведение q.

5. [895] Даны n чисел. Выделите из них группы, содержащие от 1 до n элементов, каждая из которых имеет сумму, равную простому числу.

6. [806] Найдите все тройки элементов данного одномерного массива натуральных чисел, сумма которых кратна десяти.

7. [807] Найдите все четверки элементов данного одномерного мacсива нату­ральных чисел, произведение которых равно 120.

8. [808] Найдите все пятерки элементов данного одномерного масси­ва нату­ральных чисел, сумма которых равна числу, оканчивающе­муся на 25.

9. [809] Имеется n точек на координатной прямой. Выделите из них все пары то­чек, расстояние между которыми равно данному числу.

10. [810] Имеется n точек на координатной плоскости. Выделите из них все пары точек, расстояние между которыми равно данному числу.