2.5 Знакопеременные ряды

Определение 1. Числовые ряды, члены которых как положительные числа, так и отрицательные, называются знакопеременными.

Знакочередующиеся ряды

являются частным случаем рядов знакопеременных.

Определение 2. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд называется условно или неабсолютно сходящимся.

Теорема

Если сходится ряд, составленный из абсолютных величин членов данного ряда, то сходится и данный ряд, называемый в этом случае абсолютно сходящимся.

Теорема Лейбница (достаточный признак сходимости знакочередующегося ряда)

Если абсолютные величины членов знакочередующегося ряда , монотонно убывают и абсолютная величина общего члена ряда стремится к нулю при, то ряд сходится, его сумма положительна и меньше первого члена.

Следствие. При замене суммы ряда частичной суммой мы отбрасываем все члены ряда начиная с, т.е. отбрасываем знакочередующийся ряд, который удовлетворяет признаку Лейбница. Сумма этого ряда по абсолютной величине меньше модуля первого члена ряда, т.е. меньше. Значит, абсолютная величина допущенной ошибки при такой замене на будет меньше абсолютной величины первого члена отброшенной части ряда.

Примечания:

1. Исследование сходимости знакопеременных рядов следует начинать с исследования их абсолютной сходимости, так как это часто приводит быстрее к цели, чем применение признака Лейбница с последующим выяснением абсолютной сходимости ряда.

2. Для знакоположительных рядов мы будем применять один из пяти признаков их сходимости (пп. 2.4.1 – 2.4.4).

Задача 8.31 [7]

Исследовать на сходимость ряд .

Решение:

Этот ряд знакопеременный. Исследуем его на абсолютную сходимость. Составляя ряд из абсолютных величин (модулей) членов данного ряда, получим ряд . Применим признак Даламбера. Выпишем членыи; , .

Тогда ,

, т.е. ряд сходится. Следовательно, исходный ряд сходится абсолютно.

Задача 9.31 [7]

Вычислить сумму ряда с точностью .

, .

Решение:

Прежде чем искать приближенно сумму данного ряда, надо знать, что она действительно существует, т.е. что данный ряд сходится. Проверяем сходимость ряда по признаку Лейбница: его члены монотонно убывают по абсолютному значению (убедитесь в этом самостоятельно), и .

Находим первые члены ряда с четырьмя знаками после запятой (в приближенных вычислениях надо брать одну запасную цифру).

Получили: .

Таким образом, достаточно взять первые три члена ряда, чтобы его сумма удовлетворяла заданной точности.

.

Согласно следствию из теоремы Лейбница, допущенная ошибка вычисления суммы ряда меньше 0,001.

Задача 10.31 [7]

Доказать справедливость равенства .

Решение:

Рассмотрим ряд . Исследуем его на сходимость, применяя признак Даламбера: ,.

, ряд сходится.

Тогда по необходимому признаку сходимости числового ряда следует, что его -й член стремится к нулю при , т.е. .

3 Функциональные ряды

Рассмотрим ряд

, (7)

где все функции определены в одном и том же промежутке, называемом областью определения ряда. Придавая аргументуопределенные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися.

Совокупность тех значений х, при которых функциональный ряд сходится, называется областью его сходимости.

В области сходимости сумма функционального ряда является некоторой функцией от х:

, (8)

где , х принадлежит области сходимости ряда (7).

Разность (9)

называется n-м остатком ряда.

Так как исследование сходимости функциональных рядов сводится к исследованию сходимости числовых рядов, то для нахождения областей сходимости функциональных рядов можно применять достаточные признаки сходимости числовых рядов. При этом различают области абсолютной и условной сходимости функционального ряда.

Задача 11.31 [7]

Найти область сходимости функционального ряда .

Решение:

Рассмотрим ряд . Сравним его с числовым рядом, используя второй признак сравнения (п. 2.4.1). Найдем предел частного общих членов этих рядов при :

.

Следовательно, ряд расходится, так как расходится гармонический ряд. Далее воспользуемся теоремой: если рядрасходится и (с – какое-либо фиксированное число), то ряд также расходится. В данном случае,. Значит, приряд расходится. Привсе члены функционального рядаравны нулю, при , т.е. ряд сходится. Итак, данный ряд расходится при всех х, кроме .

Задача 12.31 [7]

Найти область сходимости функционального ряда .

Решение:

Применим признак Даламбера:

, ;

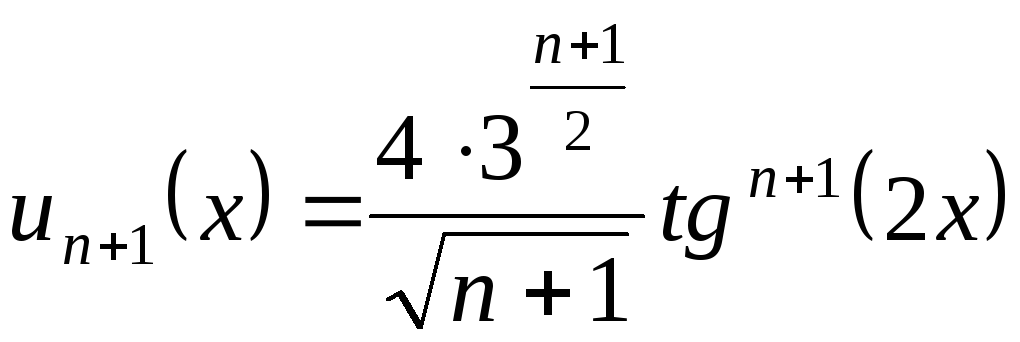Данный ряд будет сходиться, причем абсолютно, для тех значений , при которых .

Решим полученное неравенство:

;

, , .

При . Исследуем сходимость данного ряда в этих точках.

При получаем ряд .

Ряд Дирихле расходится при (см. задачу 3.31). При получим знакочередующий ряд . По признаку Лейбница он сходится, но не абсолютно.

Таким образом, данный ряд сходится при , .

Задача 13.31 [7]

Найти область сходимости функционального ряда

Решение:

Члены данного ряда определены на всей числовой оси, за исключением . Эта точка не принадлежит области определения ряда. Исследуем ряд на сходимость с помощью радикального признака Коши.

.

Найдем .

при всех допустимых значениях х. Итак, данный ряд сходится при всех х, кроме х = 0.

Задача 14.31 [7]

Найти область сходимости функционального ряда .

Решение:

Воспользуемся признаком Даламбера:

, ;

.

При m < 1 данный ряд будет сходиться, т.е. x² < 1, | x | < 1,

–1 < x < 1.

Исследуем границы интервала . При получим ряд, который расходится, так как (см. п. 2.3). Следовательно, областью сходимости данного ряда является интервал .