1.1 О рядах

В «бесконечной» сумме процесс сложения никогда не кончается, за каждым слагаемым всегда стоит следующее.

Ряд

(его члены образуют геометрическую прогрессию со знаменателем x) в случае стремится к 1/(1-x). Поэтому пишут:

или .

Сумма этого ряда была определена впервые в III в. до н.э. (из истории математики). Архимед применил суммирование бесконечной геометрической прогрессии со знаменателем 1/4.

После Архимеда вплоть до XVI в. рядами не занимались. С XVI в. началось изучение изменяющихся процессов. Для знакочередующегося ряда

Г. Лейбниц находит сумму. Она равна /4.

Л. Эйлер нашел сумму для ряда ,

, .

Это дало возможность приближенно вычислить число π с любой степенью точности (если взять достаточно много слагаемых).

Понятие сходимости ряда в XVI в. точно установлено еще не было, и считалось, что любой ряд имеет сумму и что с рядами можно выполнять такие же арифметические действия, как и с многочленами: складывать, умножать, переставлять слагаемые и т.п. И это часто приводило к фантастическим результатам. Например, получали, что сумма ряда могла быть и 0, и 1, и даже 1/2.

Рассуждения были примерно следующие:

или

.

Пусть ; перепишемS так:

, т.е. , откуда.

И только когда началось систематическое изучение рядов (начало XIX в.), было установлено, что, например, абсолютно сходящиеся ряды не меняют сумму при перестановке членов.

Идея представления функций степенными рядами принадлежит И. Ньютону. Он нашел разложения многих функций.

Например,

,

где x – радианная мера угла.

Так, ряд дает разложение функции.

Если

,

то, ограничиваясь несколькими первыми членами, мы получим приближенное представление функции: оно тем точнее, чем больше будет взято членов ряда (слагаемых).

При рассмотрении периодических процессов пользуются тригонометрическими рядами:

.

Формулы, по которым определяются коэффициенты функции, – формулы Фурье – дают название таким рядам – ряды Фурье.

2 Числовые ряды

Определение. Выражение

(1)

называется рядом, где – последовательность чисел или функций. Слагаемые– это члены ряда,– общий член ряда.

Ряд называется числовым, если все его члены являются числами.

Ряд является функциональным, если все члены ряда – функции.

2.1 Сумма ряда

Определение. Сумма конечного числа первых членов ряда называетсяn-й частичной суммой ряда:

. (2)

– первая частичная сумма,

– вторая частичная сумма,

– третья частичная сумма,

…………………………………………………………….

– n-я частичная сумма и т.д.

Определение. Если существует конечный предел последовательности частичных сумм

, (3)

то его называют суммой ряда и говорят, что ряд сходится. Если не существует, то говорят, что ряд расходится и суммы не имеет. При этом пишут:.

задача 1.31 [7]

Найти сумму ряда .

Решение:

Общий член ряда следует упростить. Представим его суммой двух простейших дробей. Знаменатель разложим на множители.

, тогда ,.

.

.

Значения коэффициентов А и В найдем устно: чтобы при сложении дробей в числителе получилось 14, надо положить А = 1, В = –1.

.

Далее найдем (для формулы (3)).

,

,

,

,

,

,

,

………………………

,

.

Чтобы вывести формулу для конечной суммы , проанализируем некоторые частичные суммы.

,

,

.

Таким образом, n-я частичная сумма

.

.

.

Задача 2.31 [7]

Найти сумму ряда .

Решение:

Как и в первой задаче, сначала упростим . Разложим правильную рациональную дробьна простейшие дроби. Такую операцию мы часто выполняли, например, при интегрировании рациональных дробей.

.

Выпишем столбцом a₁, a₂, , a₃,…, a_n. При этом расположим слагаемые с одинаковыми знаменателями друг под другом:

,

,

,

,

,

……………………………….…

,

,

.

В столбцах со знаменателями 3, 4, 5 получим соответственно: ,,и т.д.

Тогда, например, ,

и т.д.

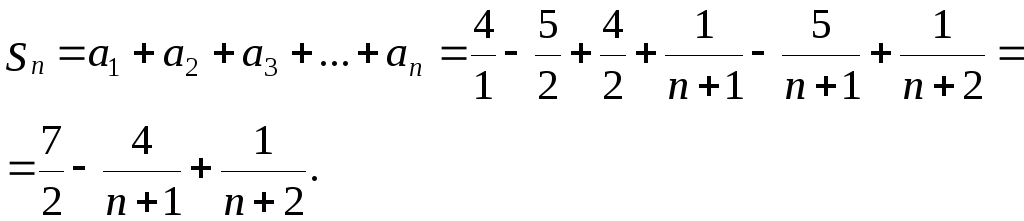
Сумма , т.е.

.

Примечание. Важнейшей задачей теории числовых рядов является вычисление их сумм. В задачах 1.31, 2.31 это можно было сделать с помощью формулы (3). Но такое нахождение суммы ряда часто требует громоздких выкладок или даже невозможно (см. задачу 3.31). Тогда пользуются различными признаками сходимости рядов. Для сходящегося ряда ограничиваются приближенным вычислением его суммы, заменяя ее частичной суммой с достаточно большим числом членов и оценивая допущенную погрешность (см. задачу 9.31).