
Kalashnikova_Nacher_geom
.pdf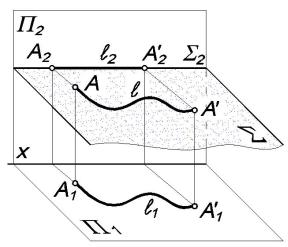
При всяком перемещении точки в плоскости, параллельной плоскости проекции П1, ее фронтальная проекция перемещается по прямой, параллельной оси проекций х.
В случае произвольного перемещения точки в плоскости, параллельной плоскости П2, ее горизонтальная проекция перемещается по
прямой, параллельной оси проекций х. |
|
Зададим плоскость Σ, параллель- |
|
ную горизонтальной плоскости про- |
|
екций П1 (рис. 7.1). Пусть точка А, |
|
принадлежащая плоскости Σ, пере- |
|
местится из положения А в положе- |
|
ние А', двигаясь в плоскости Σ по |
|
произвольной траектории ℓ. Фрон- |
|
тальная проекция точки А2 перемес- |
|
тится в положение А'2, при этом от- |
|
резок [А2А'2] принадлежит следу Σ2, |
|
который параллелен оси х. Горизон- |
Рис. 7.1 |
тальная проекция точки А1 перемещается в положение А'1 по той же произвольной траектории, что и сама точка А.
Рассмотрим основные задачи, решаемые способом плоскопараллельного перемещения. Четыре задачи, рассмотренные при изучении темы замены плоскостей проекций, можно свести к двум комбинированным.
Задача 1. Отрезок [AB] прямой общего положения перевести в положение проецирующей прямой (рис. 7.2).
Задача решается в два этапа:
1. Отрезок [АВ] переводится в положение линии уровня, т.е. параллельное плоскости проекций П2. У отрезка [АВ], параллельного плоскости П2, горизонтальная проекция должна быть параллельна оси проекций х. Поэтому переводим проекцию [А1В1] в новое положение [А'1В'1] параллельно оси х. При этом новая горизонтальная проекция [А'1В'1] равна по длине исходной [А1В1].
Фронтальные проекции точек отрезка [A2B2] будут перемещаться в новое положение по прямым, параллельным оси проекций х. Для построения фронтальной проекции отрезка в перемещенном положе-
нии [А'2В'2] из проекций А'1 и В'1 проведем линии связи, перпендикулярные к оси х, и найдем точки пересечения их с соответствующими горизонтальными прямыми, проведенными из проекций А2 и В2.
Рис. 7.2
Выполнив эти действия, мы достигли следующего: отрезок [А'В'] параллелен плоскости проекций П2;
проекция [А'2В'2] определяет натуральную величину отрезка [АВ];
угол , образованный проекцией [А'2В'2] с осью х, определяет угол наклона отрезка [АВ] к плоскости П1.
2. Отрезок [А'В'] переводится в положение проецирующей прямой.
Фронтальная проекция отрезка [А'2В'2] перемещается в новое положение [А''2В''2], перпендикулярное к оси проекций х, при этом величина отрезков [А'2В'2] и [А''2В''2] не меняется. Горизонтальная проекция отрезка [А''1В''1] находится по ранее изложенному способу. Отрезок [А''В''] перпендикулярен к плоскости П1, следовательно, имеет вырожденную горизонтальную проекцию [А''1В''1] в виде точки.
Задача 2. Плоскость Σ (ABC) общего положения перевести в положение плоскости уровня (рис. 7.3).
Задача решается в два этапа:
1. Плоскость Σ(ABC) переводится в проецирующее положение. Для этого в плоскости треугольника ABC проводим горизонталь h
через точки C и 1. Горизонтальную проекцию A1B1C1 треугольника перемещаем без изменения размеров в положение А'1В'1С'1 так, чтобы горизонтальная проекция горизонтали h'1 была перпендикулярна к
оси проекций х. Фронтальной проекцией треугольника в новом положении является прямая А'2В'2С'2, т.е. плоскость треугольника стала фронтально проецирующей.
Рис. 7.3
Выполнив эти действия, мы достигли следующего:
плоскость Σ'(A'B'C') стала перпендикулярной к фронтальной плоскости проекций П2;
угол , образованный проекцией – следом А'2В'2С'2 с осью х, равен натуральной величине угла наклона плоскости Σ к горизонтальной плоскости проекций П1.
2. Плоскость Σ'(A'B'C') переводится в положение плоскости уровня.
Фронтальную проекцию А'2В'2С'2 перемещаем в положение А''2В''2С''2, параллельное оси проекций х. Это соответствует тому, что в пространстве треугольник параллелен горизонтальной плоскости проекций П1. Проекция А''1В''1С''1 определяет натуральную величину треугольника ABC.
7.3Вращение вокруг оси, перпендикулярной к плоскости проекций
Вращение вокруг оси, перпендикулярной к плоскости проекций, является частным случаем плоскопараллельного перемещения. Отли-
чие состоит лишь в том, что за траекторию перемещения точки берется не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения.
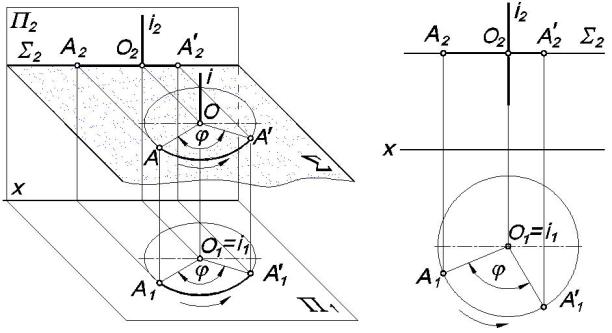
Проследим, как будет изменяться положение точки А при ее вращении вокруг оси i, перпендикулярной к плоскости П1 (рис. 7.4).
Рис. 7.4 Рис. 7.5
Точка А перемещается по дуге окружности: в плоскости Σ, перпендикулярной к оси вращения i и, следовательно, параллельной горизонтальной плоскости проекций П1. Поэтому эта окружность проецируется на плоскость П1 без искажения, а на плоскость П2 – в отрезок прямой, параллельный оси проекций х.
Таким образом, при вращении точки вокруг оси, перпендикулярной к плоскости проекций П1, горизонтальная проекция точки перемещается по окружности с центром на горизонтальной проекции оси вращения, а фронтальная – по прямой, параллельной оси проекций х (рис. 7.5).
Вращение точки вокруг оси i, перпендикулярной к фронтальной плоскости проекций, показано на рис. 7.6. Точка В перемещается в новое положение В' по окружности, принадлежащей фронтальной плоскости уровня . Фронтальная проекция
точки перемещается по окружности, центр которой принадлежит фронтальной проекции оси вращения, а горизонтальная проекция точки – по прямой, параллельной оси х.
Задача 7.3.1. Отрезок [АВ] прямой общего положения перевести в положение прямой, перпендикулярной к плоскости проекций П2
(рис. 7.7). |
|
|
|
Чтобы осуществить |
переме- |
|
|
щение отрезка из общего в про- |
|
||
ецирующее положение, необхо- |
|
||
димо последовательно |
выпол- |
|
|
нить два вращения вокруг осей, |
|
||
перпендикулярных к плоскостям |
|
||
проекций. После первого пере- |
|
||
мещения отрезок переводится в |
|
||
положение, параллельное плос- |
|
||
кости П1, и лишь после этого |
|
||
вращением вокруг оси, перпен- |
Рис. 7.7 |
||
дикулярной к плоскости |
проек- |
||
|
|||
ций П1, перемещают отрезок в положение, перпендикулярное к плоскости П2. На рис. 7.7 отрезок [AB] вначале вращением вокруг оси вращения i П2 переведен в положение, параллельное плоскости П1 ([А'2В'2] || x). Затем вращением вокруг оси i' П1 отрезок [AB] перемещен во фронтально проецирующее положение ([А''1В''1] x). Для упрощения геометрических построений ось вращения следует выбирать так, чтобы она пересекала вращаемую прямую.
В случае перевода плоскости общего положения в частное задача решается аналогично вышерассмотренным примерам. Чтобы плоскость, произвольно расположенная в пространстве, заняла проецирующее положение, достаточно плоскость повернуть до того положения, когда линия уровня, принадлежащая этой плоскости, станет перпендикулярна к плоскости проекций.
Задача 7.3.2. Определить угол наклона плоскости Σ (ABC) к горизонтальной плоскости проекций (рис. 7.8).
Для решения задачи плоскость Σ необходимо перевести в положение фронтально проецирующей. Проведем в плоскости Σ горизонталь h.
Вращением вокруг оси i, проходящей через горизонталь h и пер-
|
пендикулярной к |
плоскости |
||
|
П1, горизонталь переводится в |
|||
|
положение h' (h'1; h'2) |
и рас- |
||
|
полагается перпендикулярно к |
|||
|
плоскости П2. При повороте |
|||
|
горизонтали на угол φ на та- |
|||
|
кой же угол повернется все |
|||
|
множество точек этой плоско- |
|||
|
сти. Поэтому для определения |
|||
|
нового положения проекций |
|||
|
треугольника ABC достаточно |
|||
|
повернуть вокруг оси точки А, |
|||
|
В, С на тот же угол φ. |
|
||
|
По горизонтальным |
про- |
||
|
екциям А'1В'1С'1 |
определяем |
||
|
их фронтальные проекции. На |
|||
|
плоскости П2 |
треугольник |
||
|
А'В'С' проецируется в линию. |
|||
|
Отсюда определяем величину |
|||
|
угла α. |
|
|
|
Рис. 7.8 |
Задача 7.3.3. |
Определить |
||
угол наклона плоскости Σ, за- |
||||
|
||||
данной следами, к плоскости П2 (рис. 7.9).
Поскольку плоскость Σ задана следами, выберем ось вращения i, расположенную в плоскости П1. Тогда ось i имеет со следом Σ1 общую точку 2. Из фронтальной проекции оси i2 опускаем перпендикуляр на след Σ2 и поворачиваем его
|
до совмещения с осью х. |
|||
|
Через точку 1'2 |
проводим новое |
||
|
положение фронтального следа Σ2' |
|||
|
перпендикулярно |
к |
повернутому |
|
|
перпендикуляру. |
Горизонтальный |
||
|
след находим с помощью точки 2. |
|||
|
Угол β – искомый. |
|
|
|
|
Весьма важным в инженерной |
|||
|
практике |
является |
исследование |
|
|
траекторий |
точек |
|
вращающихся |
Рис. 7.9 |
элементов конструкций. |
|||
Задача 7.3.4. |
Вращением вокруг оси i точку А ввести в плос- |
||
кость Σ (рис. 7.10). |
|
||
Точка А вращается вокруг оси |
|||
в горизонтальной |
плоскости . |
||
Центром |
вращения |
является |
|
точка О, радиусом вращения – от- |
|||
резок [ОА]. Плоскость |
пересека- |
||
ет данную плоскость Σ по гори- |
|||
зонтали h. Дуга окружности тра- |
|||
ектории движения точки А пе- |
|||
ресекает |
данную |
горизонталь в |
|
точке А' (вторая точка не по- |
|
казана). |
|
Точка А' является искомой. |
Рис. 7.10 |
7.4Вращение вокруг оси, параллельной плоскости проекций (вращение вокруг линии уровня)
Эффективным способом, упрощающим решение задач, связанных с определением метрических характеристик плоских фигур, является способ вращения этих фигур вокруг их линий уровня. Путем такого вращения можно плоскость, которой принадлежит рассматриваемая фигура, повернуть в положение, параллельное плоскости проекций. В этом случае ортогональная проекция любой принадлежащей плоскости фигуры будет равна оригиналу и, следовательно, позволит определить все метрические характеристики проецируемой фигуры непосредственно по ее проекции без каких-либо дополнительных построений.
Вращая плоскость вокруг горизонтали, можно перевести ее в положение, параллельное плоскости П1, и получить неискаженный вид геометрической фигуры на горизонтальной проекции. Вращение плоскости вокруг фронтали позволяет перевести ее в положение, параллельное плоскости П2, что обеспечит получение неискаженного вида фигуры на фронтальной проекции. Каждая точка плоскости при ее вращении перемещается по окружности, принадлежащей плоско-
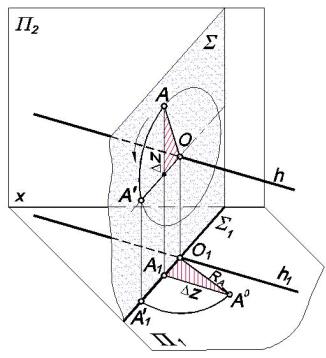
сти, перпендикулярной к оси вращения. Центр окружности будет расположен на оси вращения, а величина радиуса вращения равна расстоянию от точки до оси вращения. Если за ось вращения взята горизонталь, то окружность, представляющая траекторию движения точки, будет проецироваться на плоскость П1 в отрезок прямой, перпендикулярной к горизонтальной проекции горизонтали. Точка пересечения горизонтальных проекций горизонтали и окружности определяет горизонтальную проекцию центра вращения.
|
Точка А при вращении во- |
|||||
|
круг горизонтали h будет пере- |
|||||
|
мещаться по окружности, плос- |
|||||
|
кость которой Σ перпендику- |
|||||
|
лярна к |
оси |
вращения |
h |
||
|
(рис. 7.11). Чтобы переместить |
|||||
|
точку в новое положение путем |
|||||
|
поворота ее вокруг горизонтали, |
|||||
|
необходимо |
найти |
положение |
|||
|
центра вращения и определить |
|||||
|
величину |
радиуса |
вращения. |
|||
|
Центр вращения точка О нахо- |
|||||
|
дится в точке пересечения оси |
|||||
Рис. 7.11 |
вращения |
h |
с |
плоскостью |
Σ. |
|
|
||||||
Чтобы определить величину радиуса вращения |ОА|, необходимо построить в плоскости П1 прямоугольный треугольник О1А1А0. Для этого принимаем горизонтальную проекцию O1A1 за катет прямоугольного треугольника, второй катет равен разности аппликат концов отрезка [OA]: ZA - ZO = Z. Гипотенуза треугольника О1А1А0 – отрезок [O1A0] – равна искомому радиусу R. Новое, после поворота, положение точки A'1 находится в месте пересечения дуги окружности, проведенной из горизонтальной проекции центра вращения O1 радиусом, равным |O1A0|, с горизонтальным следом Σ1 плоскости Σ.
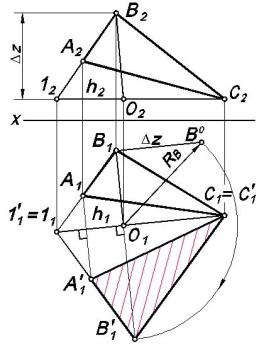
На рис. 7.12, а преобразования, описанные выше, выполнены на проекционном чертеже. На рис. 7.12, б показано вращение точки В вокруг фронтали f.
а |
б |
Рис. 7.12
Рассмотрим задачи, которые наиболее целесообразно решать способом вращения вокруг линии уровня.
Задача 7.4.1. Определить натуральную величину треугольника
ABC (рис. 7.13).
Проводим в плоскости треугольника через точку С горизонталь h. Вращаем точку В вокруг горизонтали h. Для этого на чертеже через точку B1 проведем прямую, перпендикулярную к проекции горизонтали h1, и отметим точку O1 – проекцию центра вращения. Для определения натуральной величины радиуса вращения точки В строим прямоугольный треугольник О1В1В0, у которого один катет – горизонтальная проекция O1В1 отрезка [ОВ], а второй катет равен разности аппликат точек В и О. Определяем величину |O1В0| ра-
диуса вращения точки В и отклады- Рис. 7.13 ваем его от точки O1 на линии O1В1.
Для построения повернутого положения точки А нет необходимости повторять проделанные для точки В построения. Для этого доста-
точно обратить внимание на то, что точка 1, лежащая на пересечении стороны АВ с горизонталью h, не будет изменять своего положения при вращении и, следовательно, сторона А'1В'1 пройдет через эту точку. Таким образом, точка А'1 будет лежать в точке пересечения прямой 1'1В'1 с траекторией перемещения точки А1 – прямой, проходящей через точку А1 и перпендикулярной к линии h.
Соединяя точки А'1 и В'1 с неподвижной точкой С'1, получим натуральный вид треугольника ABC: А'1В'1С'1 = АВС.
Способом вращения вокруг линии уровня целесообразно пользоваться при определении величины угла:
между прямой и плоскостью;
между двумя плоскостями;
между скрещивающимися прямыми.
Эти задачи сводятся к определению угла между пересекающимися прямыми.
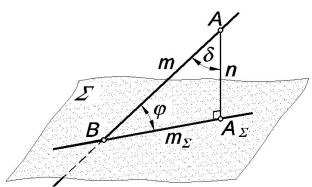
Углом между прямой и плоскостью называется угол между этой прямой и ее прямоугольной проекцией на данную плоскость
(рис. 7.14).
Рис. 7.14
плоскостью Σ.
Задача на определение угла между прямой т и плоскостью Σ имеет следующий план решения:
1.Из произвольной точки А, принадлежащей прямой m, опускаем перпендикуляр n на плоскость Σ.
2.Определяем точку AΣ пересечения перпендикуляра n с
3.Находим точку В – пересечение прямой т с плоскостью Σ.
4.Проводим линию тΣ – проекцию прямой т на плоскость Σ.
5.Угол ABAΣ – искомый.
Решение задачи может быть упрощено, если определять не угол φ
между прямой т и плоскостью Σ, а дополнительный до 90° угол |
δ. |
|
Тогда |
отпадает необходимость в нахождении точек В и |
АΣ. |
900 |
. |
|
Задача 7.4.2. Определить угол между прямой т и плоско-
стью Σ(h, f) (рис. 7.15).
