
Kalashnikova_Nacher_geom
.pdfПри этом возможны случаи:
1)прямая n параллельна прямой m, следовательно, прямая m параллельна плоскости Σ;
2)прямая n пересекает прямую m, следовательно, прямая m пересекает плоскость Σ.
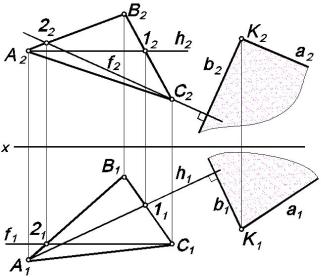
По этой схеме решим задачу на проекционном чертеже. Пусть даны плоскость Σ, заданная треугольником АВС, и прямая m. Определим точку пересечения прямой с плоскостью (рис. 4.13). Придерживаясь схемы, задачу решаем в такой последовательности:
1. Прямую m заключаем в горизонтально проецирующую плоскость , для этого через горизонтальную проекцию прямой следует
провести горизонтальный след 1 |
Рис. 4.13 |
плоскости . |
|
2.Определяем линию пересечения заданной плоскости Σ и вспомогательной проецирующей плоскости , прямая (1-2) пересечения плоскостей определяется по точкам 1 и 2 пересечения прямых АВ и ВС данной плоскости проецирующей плоскостью.
3.Определяем точку К пересечения прямой m с прямой линией (1-2) пересечения плоскостей.
Точка К является искомой точкой пересечения прямой m с плоскостью треугольника ABC. Укажем видимые и невидимые (относительно плоскостей проекций) отрезки прямой линии, применяя способ конкурирующих точек. Если смотреть по направлению проецирующей прямой, то можно увидеть ту из конкурирующих точек, которая наиболее удалена от плоскости проекций или наиболее близко расположена к наблюдателю.
Так, на горизонтально проецирующей прямой (1-3) находятся точки 1 и 3, принадлежащие прямым m и АВ. Точка 1 принадлежит стороне треугольника АВ, точка 3 – прямой m. По фронтальным про-
екциям 12 и 32 этих точек устанавливаем, что точка 1 расположена дальше, чем точка 3, относительно плоскости проекций П1. Следовательно, на участке (3-K) прямая линия m (если смотреть на горизон-
тальную плоскость проекций П1) находится под плоскостью треугольника, т.е. закрыта этим треугольником. Условно горизонтальную проекцию прямой m1 на участке (31-К1) покажем штриховой линией.
Чтобы определить видимость прямой относительно фронтальной плоскости проекций, воспользуемся фронтально проецирующей прямой (4-5). Здесь точка 5 принадлежит стороне ВС треугольника, а точка 4 – прямой m. По местоположению горизонтальных проекций этих точек устанавливаем, что точка 5 ближе к наблюдателю, чем точка 4. Поэтому на участке (К-4) (если смотреть на фронтальную плоскость проекций П2) прямая m закрыта треугольником и является
невидимой. Условно на участке (К2-42) проекцию m2 прямой покажем штриховой линией.
Рассмотрим задачу определения точки пересечения прямой m с плоскостью общего положения Σ, заданной следами
(рис. 4.14).
Порядок решения задачи аналогичен предыдущей. В результате выполненных построений находим точку К – точку пересечения прямой m с плоскостью Σ.
Рис. 4.14 |
|
|
На рис. 4.15 показано нахождение |
|
точки пересечения плоскости общего по- |
|
ложения Σ с проецирующей прямой m. В |
|
данном случае сразу определяется гори- |
|
зонтальная проекция К1 искомой точки |
|
пересечения, так как она принадлежит |
|
горизонтально проецирующей прямой m. |
|
Фронтальная проекция K2 определяется |
|
исходя из условия принадлежности точ- |
|
ки плоскости с помощью, например, |
Рис. 4.15 |
фронтали f этой плоскости. |
4.8 Пересечение двух плоскостей общего положения
Две плоскости пересекаются по прямой линии, следовательно, для определения линии пересечения достаточно найти:
а) две точки, принадлежащие одновременно каждой из двух заданных плоскостей;
б) одну точку, если известно направление линии пересечения.
В общих случаях, когда непосредственно из чертежа нельзя определить точки, принадлежащие обеим плоскостям, и неизвестно направление линии пересечения плоскостей, для построения линии пе-
ресечения применяют способ вспомогательных секущих плоскостей (или плоскостей-посредников).
Этот способ состоит из следующих этапов:
1.Ввести вспомогательную секущую плоскость частного или общего положения, пересекающуюся с двумя заданными плоскостями.
2.Построить линии пересечения введенной плоскости с каждой из заданных плоскостей.
3.Найти общую точку, принадлежащую трем плоскостям. Эта точка будет принадлежать искомой линии пересечения.
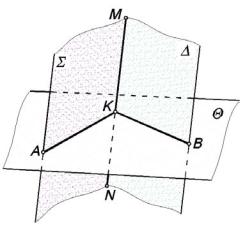
Для построения линии пересечения плоскостей Σ и (рис. 4.16) можно применить вспомогательные секущие плоскости. Точка К пересечения двух заданных плоскостей и вспомогательной Θ принадлежит линии МN пересечения заданных плоскостей:
Σ = (М N);
Σ Θ = (АК); Θ = (ВК);
К = (АК) (ВК);
К (МN).
Если одной вспомогательной плоскости недостаточно для решения задачи, то вводят еще столько плоскостей, сколько необходимо.
Рис. 4.16
В качестве плоскостей-посредников для упрощения построений чаще всего выбирают плоскости частного положения – проецирующие или плоскости уровня.
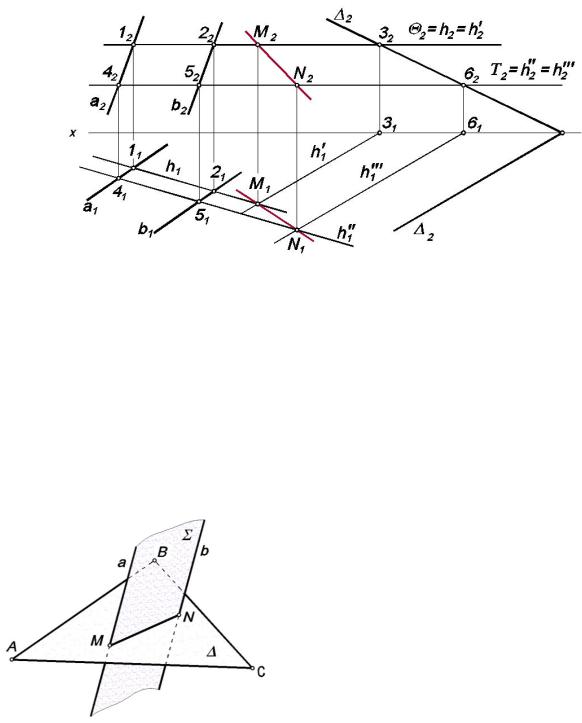
Задача 4.8.1. Построить линию пересечения плоскостей: данной параллельными прямыми а и b, и , заданной следами
(рис. 4.17).
Рис. 4.17
Σ, за-
1 и 2
Вводим вспомогательную горизонтальную плоскость уровня Θ. Она пересекает плоскость Σ по горизонтали h, проходящей через точки 1 и 2, а плоскость по горизонтали h΄, проходящей через точку 3. Горизонтали пересекаются в точке М.
Вторая секущая горизонтальная плоскость уровня Т пересекает заданные плоскости по горизонталям h˝ и h΄˝, которые в свою очередь пересекаются в точке N. Прямая (MN) является искомой линией пересечения заданных плоскостей Σ и .
Другой способ построения линии пересечения двух плоскостей заключается в том, что находят точки пересечения двух прямых, принадлежащих одной из плоскостей, с другой плоскостью (дважды решают задачу на определение точки пересечения прямой линии и плоскости) (рис. 4.18).
Плоскость Σ задана параллельными прямыми а и b, плоскость – треугольником ABC. Найдем точки
пересечения прямых а и b плоскости Σ с плоскостью треугольника ABC. Прямая а пересекает плоскость треугольника в точке М, прямая b – в точке N. Линия пересечения заданных плоскостей проходит через найденные точки М и N.
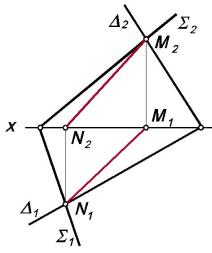
Задача 4.8.2. Построить линию пересечения плоскостей: Σ, заданной прямыми а и b, и , заданной треугольником АВС (рис. 4.19).
Найдем пересечение прямой а с |
|
||
плоскостью треугольника ABC. Через |
|
||
прямую а проводим фронтально про- |
|
||
ецирующую плоскость Г. Определяем |
|
||
линию (1-2) пересечения этой плоско- |
|
||
сти с плоскостью треугольника ABC. |
|
||
Найденная линия (1-2) пересекается с |
|
||
прямой а в точке М, которая является |
|
||
точкой пересечения линии а с плоско- |
|
||
стью . |
|
|
|
Аналогично определяем точку N – |
|
||
точку пересечения прямой b с плоско- |
|
||
стью треугольника ABC. Прямая (МN) |
|
||
является линией |
пересечения двух |
|
|
плоскостей. |
|
|
|
Видимость плоскостей |
относи- |
Рис. 4.19 |
|
|
|
|
|
тельно плоскостей |
проекций |
опреде- |
|
лена с помощью конкурирующих точек.
В частном случае, когда плоскости заданы следами, которые пересекаются в поле чертежа, решение задачи упрощается. Две точки, через которые проходит линия пересечения плоскостей, находятся как точки пересечения одноименных следов. В данном случае вспомогательными секущими плоскостями можно считать непосредственно плоскости проекций П1 и П2.
Определяют точки пересечения одноименных следов плоскостей. Эти точки, общие для двух плоскостей, являются следами линии пересечения заданных плоскостей.
Определим линию |
пересечения |
двух |
||
плоскостей |
Σ и , |
заданных |
следами |
|
(рис. 4.20). Горизонтальные следы |
Σ1 |
и 1 |
||
пересекаются в точке М, фронтальные |
||||
следы Σ2 и |
2 – в точке N. Прямая (МN) яв- |
|||
ляется линией пересечения заданных плоско- |
|
стей. |
Рис. 4.20 |
|
5 ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ, ПРЯМЫХ, ПЛОСКОСТЕЙ
5.1 Взаимно перпендикулярные прямая и плоскость
Прямая перпендикулярна к плоскости, если она перпендикулярна хотя бы к двум пересекающимся прямым, принадлежащим этой плоскости.
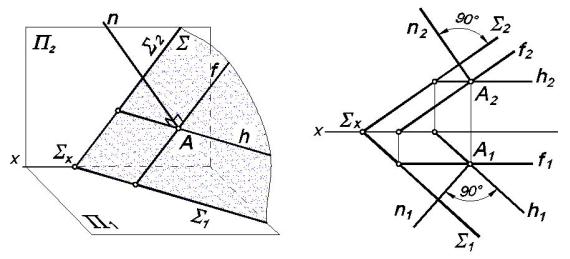
Если в плоскости взять не произвольные пересекающиеся прямые, а ее горизонталь и фронталь (рис. 5.1, а), то появляется возможность воспользоваться свойством проекции прямого угла:
прямой угол между прямой n и горизонталью h проецируется без искажения на плоскость П1;
прямой угол между прямой n и фронталью f проецируется без искажения на плоскость П2.
а |
б |
Рис. 5.1
Отсюда вытекает следующее свойство: прямая линия перпендикулярна к плоскости, если ее горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция перпендикулярна к фронтальной проекции фронтали плоскости (рис. 5.1, б).
n1 h1; n2 f2 .
Если плоскость задана следами (линии уровня проводить не обязательно), то горизонтальная проекция n1 перпендикулярна к горизонтальному следу Σ1, а фронтальная проекция перпендикуляра n2 – к фронтальному следу Σ2:
n1 Σ1; n2 Σ2 .

Задача 5.1.1. Определить расстояние от точки А до плоскости Σ, заданной следами (рис. 5.2).
Данная задача решается в три этапа:
1. Построим проекции перпендикуляра n из точки А на плоскость Σ:
n1 Σ1; n2 Σ2.
2.Находим точку В пересечения перпендикуляра n с плоскостью Σ (по схеме задачи о пересечении прямой и плоскости).
3.Находим длину отрезка [AB] методом прямоугольного треуголь-
ника. Отрезок [A1B0] определяет расстояние от точки А до плоскости Σ.
Задача 5.1.2. |
Определить расстояние от точки А до плоскости |
|
треугольника ВСD (рис. 5.3). |
|
|
Условие задачи аналогично пре- |
|
|
дыдущей, иначе задана плоскость – не |
|
|
следами, а плоской фигурой. |
|
|
Для того чтобы опустить перпен- |
|
|
дикуляр из точки А на плоскость тре- |
|
|
угольника ВСD, в плоскости тре- |
|
|
угольника надо провести горизон- |
|
|
таль h и фронталь f. Проанализировав |
|
|
условие, видим, что горизонталью |
|
|
плоскости является сторона ВD тре- |
|
|
угольника ВСD, а фронталью – сторо- |
|
|
на ВС. Проекции перпендикуляра |
|
|
строим следующим образом: |
Рис. 5.3 |
|
n1 (В1D1); |
n2 (В2С2). |
|
Далее решение задачи аналогично предыдущей.
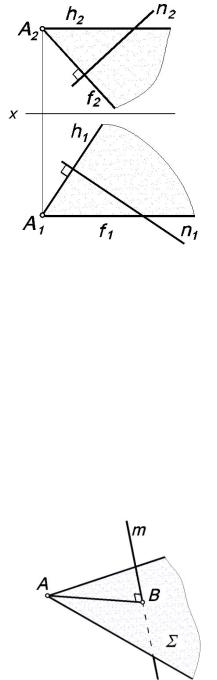
Задача 5.1.3. Рассмотрим обратную задачу. Через точку А провести плоскость, перпендикулярную к прямой n (рис. 5.4).
Через точку А проведем линии уровня – горизонталь и фронталь – перпендикулярно к прямой n:
h1 n1, |
h2 || x; |
f2 n2, |
f1 || x. |
Данные горизонталь и фронталь определяют искомую плоскость.
Рис. 5.4
5.2 Взаимно перпендикулярные прямые
Две прямые взаимно перпендикулярны, если через каждую из них можно провести плоскость, перпендикулярную ко второй прямой.
Через точку можно провести бесчисленное множество прямых, перпендикулярных к данной прямой, но только одна из них будет пересекать данную под прямым углом. Все эти прямые принадлежат одной плоскости.
Задача, в которой требуется опустить перпендикуляр из точки А на прямую m общего положения, решается по следующей схеме (рис. 5.5):
1. Через точку А провести плоскость Σ перпендикулярно к заданной прямой m.
2. Определить точку В пересечения прямой m с плоскостью Σ.
Рис. 5.5 |
3. Через точки А и В построить пер- |
|
пендикуляр из точки А на прямую m. |
||
|
||
Задача 5.2.1. Определить расстояние от точки А до прямой m |
||
(рис. 5.6). |
|
|
Задача решается по предложенной выше схеме:
1.Через точку А проведем плоскость Σ, заданную горизонталью h
ифронталью f, перпендикулярно к прямой m:
h1 m1, |
h2 || x; |
f2 m2, |
f1 || x. |
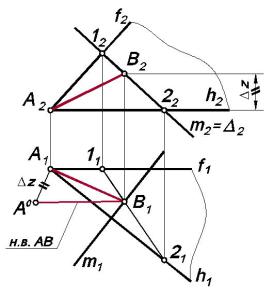
2.Определим точку В пересечения прямой m с плоскостью Σ.
3.Найдем длину отрезка [AB] методом прямоугольного треуголь-
ника.
Задача 5.2.2. Построить недостающую проекцию прямой b, если известно, что в пространстве прямые
аи b взаимно перпендикулярны
(рис. 5.7, а).
Для решения задачи используется условие перпендикулярности двух прямых.
Через точку К проводим плоскость Σ, перпендикулярную к прямой а, задаем ее горизонталью h и
фронталью f (рис. 5.7, б).
Рис. 5.6
а |
б |
Рис. 5.7
Если прямая b перпендикулярна к прямой а, то она должна лежать в построенной плоскости Σ. Горизонтальную (недостающую) проекцию b1 прямой b находим с помощью точки 3, принадлежащей произвольной линии (1-2) плоскости Σ.
5.3 Взаимно перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из плоскостей содержит прямую линию, перпендикулярную к другой плоскости.
Для построения плоскости, перпендикулярной к другой плоскости, достаточно определить прямую, перпендикулярную к этой плоскости. Через прямую можно провести множество плоскостей. Чтобы конкретизировать ответ, необходимо указать дополнительные условия.
Задача. Через прямую а провести плоскость , перпендикулярную к плоскости Σ, заданной треугольником АВС
(рис. 5.8).
В плоскости Σ проводим линии уровня – горизонталь h и фронталь f . На прямой а выбираем произвольную точку К и из нее опускаем перпендикуляр на заданную плоскость Σ:
Рис. 5.8 |
b1 h1; b2 f2. |
Линии а и b определяют искомую плоскость . |
|
|
На рис. 5.9 показана фронтально |
|
проецирующая плоскость , проходя- |
|
щая через точку В и перпендикуляр- |
|
ная к плоскости Σ. |
|
Отличительной особенностью чер- |
|
тежа, на котором заданы две взаимно |
|
перпендикулярные плоскости, из ко- |
|
торых одна – фронтально проецирую- |
|
щая, является перпендикулярность их |
Рис. 5.9 |
фронтальных следов. |
