
Kalashnikova_Nacher_geom
.pdf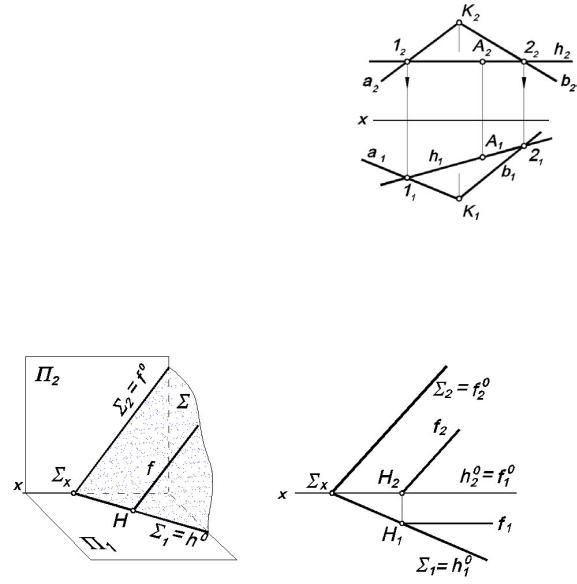
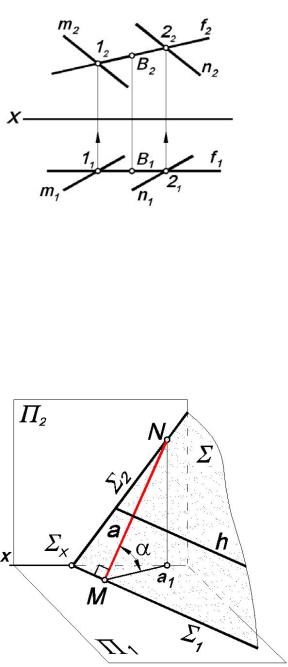
Горизонталь плоскости всегда параллельна горизонтальному следу плоскости (рис. 3.17, а). Горизонтальный след плоскости Σ1 можно обозначить как «нулевую» горизонталь h0. Характерной особенностью горизонтали является то, что ее горизонтальная проекция параллельна горизонтальному следу плоскости, а фронтальная параллельна
оси проекций х (рис. 3.17, б): |
|
h1 Σ1; |
h2 x. |
Задача 3.5.1. В плоскости , заданной |
|
пересекающимися прямыми a и b, через точку А провести горизонталь (рис. 3.18).
Фронтальную проекцию горизонтали h2 проводим через заданную проекцию А2 параллельно оси х: h2 x.
Горизонтальную проекцию h1 находим с помощью точек 1 и 2. Горизонтальная проекция точки А принадлежит горизонтальной проекции горизонтали: А1 h1.
Фронталь плоскости – это прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций. Обозначают фронталь буквой f (рис. 3.19).
а |
б |
|
Рис. 3.19 |
Фронталь параллельна фронтальному следу плоскости (рис. 3.19, а). |
|
Фронтальный след плоскости |
Σ2 можно обозначить как «нулевую» |
фронталь f 0. Характерной особенностью фронтали является то, что ее горизонтальная проекция параллельна оси проекций х, а фронтальная параллельна фронтальному следу плоскости (рис. 3.19, б):
f1 x; f2 Σ2.
|
Задача 3.5.2. |
В плоскости |
, заданной |
|
параллельными |
прямыми m и |
n, через |
|
точку B построить фронталь (рис. 3.20). |
||
|
Горизонтальную проекцию фронтали f1 |
||
|
проводим через заданную проекцию B1 |
||
|
параллельно оси х: f1 x. |
|
|
|
Фронтальную проекцию f2 |
находим с |
|
|
помощью точек 1 и 2. Фронтальная проек- |
||
Рис. 3.20 |
ция точки В принадлежит фронтальной |
||
|
проекции фронтали: В2 f2. |
|
|
Очевидно, что через каждую точку плоскости можно провести одну горизонталь h и одну фронталь f. Вообще же в плоскости можно провести множество горизонталей и фронталей. Все горизонтали плоскости параллельны между собой, так же как и параллельны все фронтали.
Линией наибольшего наклона
плоскости к плоскости проекций является прямая, образующая с плоскостью проекций наибольший угол.
С помощью линий наибольшего наклона определяют углы наклона плоскости к плоскостям проекций.
Линию наибольшего наклона плоскости к горизонтальной плоскости проекций называют линией ската плоскости.
Рис. 3.21 Представление о линии наибольшего наклона плоскости дает рис. 3.21, на котором показана прямая а – линия наибольшего наклона
плоскости к горизонтальной плоскости проекций (линия ската). Отличительной особенностью является то, что линия ската плоскости пер-
пендикулярна к горизонтали плоскости или ее горизонтальному следу.
На рис. 3.21 прямая а h является линией наибольшего наклона плоскости к плоскости П1. Из всех прямых, принадлежащих плоскости, она образует наибольший угол с плоскостью П1. Поэтому угол α является линейным углом двугранного угла, образуемого плоскостями Σ и П1.
На проекционном чертеже горизонтальная проекция линии наибольшего наклона плоскости к горизонтальной плоскости проекций П1 всегда перпендикулярна к горизонтальной проекции горизонтали этой плоскости.
Если прямая перпендикулярна к фронтали f, то она образует наибольший угол с плоскостью П2. Линия наибольшего наклона плоскости к фронтальной плоскости проекций П2 имеет фронтальную проекцию, перпендикулярную к фронтальной проекции фронтали этой плоскости.
Плоскость на чертеже можно задать проекциями одной из принад-
лежащих ей линий наибольшего наклона. |
|
||
Задача 3.5.3. |
Определить углы наклона плоскости к плоскостям |
||
проекций П1 и П2. |
|
|
|
Для определения |
угла |
|
|
наклона плоскости Σ к гори- |
|
||
зонтальной плоскости |
про- |
|
|
екций П1 построим линию |
|
||
ската а (рис. 3.22) |
|
|
|
Горизонтальная проек- |
|
||
ция линии ската а1 перпен- |
|
||
дикулярна к горизонтально- |
|
||
му следу Σ1, ее фронтальная |
|
||
проекция находится из усло- |
|
||
вия принадлежности прямой |
|
||
плоскости с помощью точек |
|
||
1 и 2. Определяем методом |
Рис. 3.22 |
||
прямоугольного |
треуголь- |
|
|
ника длину отрезка [1-2] и величину угла его наклона к плоскости П1
– угол α. Данный угол α определяет угол наклона плоскости Σ к горизонтальной плоскости проекций.
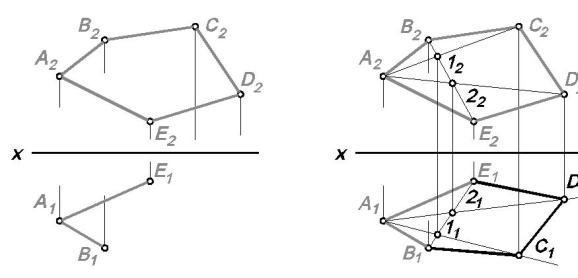
Для определения угла наклона плоскости Σ к фронтальной плоскости проекций П2 строим линию наибольшего наклона плоскости Σ к плоскости П2 – прямую b. Фронтальная проекция этой линии перпендикулярна к фронтальному следу плоскости Σ, а горизонтальная определяется с помощью точек 2 и 3. Методом прямоугольного треугольника определяем величину угла наклона прямой b к плоскости П2. Данный угол β и определяет угол наклона плоскости Σ к фронтальной плоскости проекций.
3.6Построение проекций плоских фигур
Любая из точек плоской фигуры (треугольника, квадрата, окружности и т.п.) принадлежит плоскости этой фигуры. Поэтому проекции плоской фигуры строят по условию принадлежности точек фигуры ее плоскости.
На рис. 3.23 показано построение недостающей горизонтальной проекции многоугольника ABCDE. Здесь плоскость многоугольника представлена двумя его сторонами АЕ и АВ (рис. 3.23, а).
а |
б |
|
Рис. 3.23 |
Построим в плоскости многоугольника диагональ BE (ее проек-
ции B1E1 и B2E2) (рис. 3.23, б).
На фронтальной проекции диагонали A2C2 и A2D2 пересекают диагональ B2E2 соответственно в точках 12 и 22. Найдем горизонтальные проекции точек 11 и 21 на горизонтальной проекции диагонали B1E1. Через точки 11 и 21 построим горизонтальные проекции диагоналей, на которых расположены проекции вершин C и D. Точки C1 и D1 находим с помощью линий связи.
4ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ, ПРЯМОЙ ЛИНИИ И ПЛОСКОСТИ
4.1 Относительное положение двух плоскостей
Две плоскости в пространстве могут занимать относительно друг друга следующие положения:
а) быть параллельными (частный случай параллельных плоскостей – плоскости совпадающие);
б) быть пересекающимися (частный случай – плоскости взаимно перпендикулярные).
4.2 Относительное положение прямой линии и плоскости
Прямая линия и плоскость в пространстве относительно друг друга могут занимать следующие положения:
а) прямая линия параллельна плоскости (частный случай – прямая лежит в плоскости);
б) прямая пересекается с плоскостью (частный случай – прямая перпендикулярна к плоскости).
4.3 Взаимная параллельность плоскостей
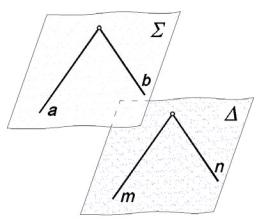
Из элементарной геометрии известна теорема признака парал-
лельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны (рис. 4.1).
Следовательно, чтобы построить
плоскость , параллельную плоскости |
|
Σ, достаточно провести через задан- |
|
ную точку две прямые, соответственно |
|
параллельные каким-нибудь двум пе- |
|
ресекающимся прямым, принадлежа- |
|
щим плоскости Σ. |
Рис. 4.1 |
Задача 4.3.1. Через точку K провести плоскость, параллельную плоскости Σ, заданной пересекающимися прямыми а и b (рис. 4.2).
Проведем через точку К прямые m и n, соответственно параллельные прямым
а и b:
m1 a1; n1 b1; m2 a2; n2 b2.
Прямые m и n определяют плоскость, проходящую через точку К и параллельную плоскости Σ.
Если плоскости заданы следами или линиями уровня (горизонталью и фронталью), то для условия параллельности плоскостей достаточно, чтобы
их следы или линии уровня были между собой параллельны.
Задача 4.3.2. Через точку K провести плоскость , параллельную плоскости Σ, заданной следами Σ1 и Σ2 (рис. 4.3).
Проведем через точку К одну из линий уровня плоскости, например, горизонталь h. Через фронтальный след горизонтали – точку F – проходит фронтальный след искомой плоскости 2, параллельно одноименному следу Σ2 заданной плоскости.
Горизонтальный след 2 параллелен следу данной плоскости Σ1 и проходит через точку пересечения фронтального следа искомой плос-
кости с осью проекций х (точку схода следов).
4.4 Взаимная параллельность прямой линии и плоскости
Прямая параллельна плоскости, если она параллельна любой прямой этой плоскости.
Через каждую точку пространства можно провести бесчисленное множество прямых, параллельных данной плоскости. Для получения единственного решения необходимо задать дополнительные условия.
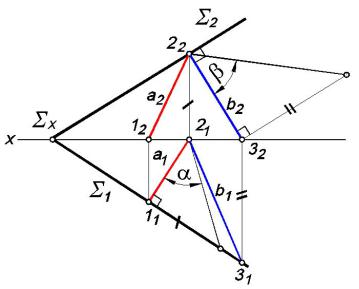
Задача 4.4.1. Доказать параллельность прямой m и плоскости , заданной двумя параллельными прямыми а и b (рис. 4.4, а).
Проведем в плоскости прямую (1-2). Ее фронтальная проекция (12 - 22) по построению параллельна фронтальной проекции m2 прямой m (рис. 4.4, б). Горизонтальную проекцию (12 - 22) построим
из условия принадлежности прямой (1-2) плоскости . |
|
|||
Проверяем |
параллель- |
|
|
|
ность горизонтальных проек- |
|
|
||
ций прямой m и (1-2). |
|
|
||
Прямая |
m параллельна |
|
|
|
плоскости , так как она па- |
|
|
||
раллельна прямой (1-2) этой |
|
|
||
плоскости: |
|
|
|
|
m1 || (11 - 21); |
|
|
|
|
m2 || (12 - 22). |
а |
|
б |
|
|
|
|
||
|
|
Рис. |
4.4 |
|
Задача 4.4.2. Через прямую а провести плоскость |
, параллель- |
|||
ную заданной прямой k (рис. 4.5). |
|
|
||
Для решения |
задачи достаточно |
|
|
|
взять на прямой а произвольную точку |
|
|
||
М (M1 a1, |
M2 a2) и провести через нее |
|
|
|
прямую b, параллельную прямой k: |
|
|
||
|
b1 || k1; |
b2 || k2. |
|
|
Пересекающиеся прямые а и b опре- |
|
|
||
деляют искомую плоскость . |
Рис. |
4.5 |
||
4.5 Пересечение прямой линии с проецирующей плоскостью
При рассмотрении проецирующих плоскостей установлена важная для них особенность. Любая геометрическая фигура, расположенная в проецирующей плоскости, имеет одну из своих проекций на соответствующем следе этой плоскости.
Это свойство проецирующих плоскостей дает возможность легко решать задачи на построение точек пересечения прямых линий про-
ецирующими плоскостями.
Точка пересечения прямой линии m горизонтально проецирующей плоскостью Σ (рис. 4.6, а) определяется следующим образом. В
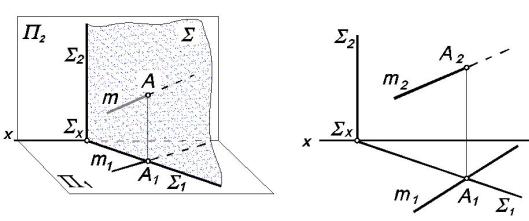
точке пересечения горизонтального следа плоскости Σ1 и горизонтальной проекции прямой m1 находим горизонтальную проекцию А1 точки А, принадлежащей данной прямой m.
а |
б |
|
Рис. 4.6 |
Фронтальная проекция точки А2 определяется как недостающая проекция точки А, принадлежащей прямой m (рис. 4.6, б). Луч прямой m, расположенный правее точки А, на фронтальной проекции изображается как невидимый, так как он расположен за плоскостью Σ, что видно на горизонтальной проекции.
На рис. 4.7 показано построение точки пересечения прямой n фронтально проецирующей плоскостью , заданной треугольником АВС.
Для этого сначала находим фронтальную проекцию К2 точки К на пересечении фронтальной проекции n2 прямой n с фронтальной проекцией (следом 2) плоскости. Горизонтальная проекция K1 точки К определяется на пересечении линии связи с горизонтальной проекцией n1 прямой n. Видимость устанавливается следующим образом: часть пря-
мой, расположенная правее точки К, находится под плоскостью треугольника ABC, поэтому на горизонтальной проекции она невидима.
4.6Пересечение плоскости общего положения с проецирующей плоскостью
Линия пересечения плоскости общего положения с проецирующей плоскостью определяется по точкам пересечения двух любых прямых линий плоскости общего положения проецирующей плоскостью.
Пусть произвольно расположенная плоскость, заданная треугольником ABC, пересекается горизонтально проецирующей плоскостью Σ (рис. 4.8). Находим точки 1 и 2 пе-
ресечения прямых AВ и ВС плоскости
треугольника ABC с горизонтально- проеци-рующей плоскостью Σ. Прямая (1- 2) является линией пересечения плоскостей. По горизонтальной проекции видно, что часть плоскости с вершиной В расположена за плоскостью Σ, следовательно, на фронтальной проекции она не видна.
На рис. 4.9 показано построение линии пересечения горизонтально проецирующей плоскости Σ с фронтально проецирующей плоскостью .
Линию (1-2) пересечения двух проецирующих плоскостей определяют, исходя из основного свойства этих плоскостей: горизонтальная проекция (11-21) прямой (1-2) должна принадлежать горизонтальному следу Σ1 плоскости Σ, а фронтальная проекция (12-22) этой прямой
– фронтальному следу 2 плоскости .
На рис. 4.10 показано построение линии пересечения двух горизонтально проецирующих плоскостей Σ и . Эти плоскости пересекаются по прямой а, перпендикулярной к горизонтальной плоскости проекций.
Рис. 4.8
Рис. 4.9
Рис. 4.10
На рис. |
4.11 построена линия пересечения плоскостей Σ и . |
||
Плоскость |
Σ является |
плоскостью |
общего положения, плоскость |
– плоскостью уровня (дважды проецирующей). |
|||
|
|
Если одна из пересекающихся плоско- |
|
|
|
стей является плоскостью уровня, плоско- |
|
|
|
сти пересекаются по линии уровня. В дан- |
|
|
|
ном случае плоскости пересекаются по го- |
|
|
|
ризонтали h. Эта горизонталь h проходит |
|
|
|
через точку N пересечения фронтальных |
|
Рис. 4.11 |
следов Σ2 и |
2. |
|
4.7Пересечение прямой линии с плоскостью общего положения
Задача на построение точки пересечения прямой линии с плоскостью общего положения является весьма важной среди других позиционных задач курса начертательной геометрии.
Иногда на чертеже нельзя непосредственно установить взаимное положение прямой линии и плоскости. В этом случае прибегают к вспомогательным построениям. В результате данных построений от вопроса о взаимном положении прямой линии и плоскости переходят
квопросу о взаимном положении двух прямых линий.
Взадачах этого типа используют способ вспомогательных плоско-
стей, который заключается в следующем (рис. 4.12):
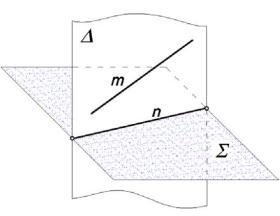
1.Через данную прямую m проводят вспомогательную плоскость . При этом подбор вспомогательных плоскостей ведется таким образом, чтобы решение задачи было наиболее простым.
2.Строят линию n пересечения плоскостей – заданной Σ и вспомогательной .
3.Устанавливают взаимное положение прямой m и линии пересе-
Рис. 4.12 |
чения плоскостей n. |
