Kalashnikova_Nacher_geom

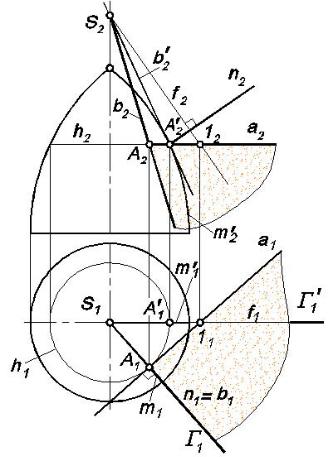
Задача 10.4.4. Провести через точку А касательную плоскость и нормаль к поверхности вращения (рис. 10.14).

Выберем пару наиболее простых линий, проходящих через заданную точку. Это будут параллель и меридиан. Касательная плоскость определяется двумя касательными а и b, проведенными в точке А к параллели и меридиану поверхности Ф. Проекции касательной а к параллели n поверхности Ф будут расположены: а1 – перпендикулярно к S1A1, а2 – параллельно оси х. Горизонтальная проекция касательной b1 к меридиану m поверхности Ф, проходящему через точку А, совпадет с горизонтальной проекцией меридиана. Чтобы найти

фронтальную проекцию касательной b2, меридиональную плоскость Г, проходящую через точку А, вращением вокруг оси поверхности Ф переводим в положение Г′, параллельное плоскости П2. В этом случае точка A перемещается в положение A′ (А′1, А′2) и будет лежать на главном меридиане. Построим в ней касательную b′2 и отметим ее точку пересечения с осью поверхности вращения – точка S (S1, S2).

Если мы теперь возвратим плоскость Г в первоначальное положение, то точка S останется на месте, как принадлежащая оси вращения, a фронтальная проекция касательной b′2 переместится в положение b2 и определится прямой (А2S2).

Для построения нормали к поверхности Ф в точке А определяем положение линий уровня в касательной плоскости, горизонталью плоскости является линия а, фронталь строим с помощью точек S и 1. Проекции нормали проводятся следующим образом: n1 a1 ; n2 f2 .

10.5 Пересечение прямой линии с поверхностью

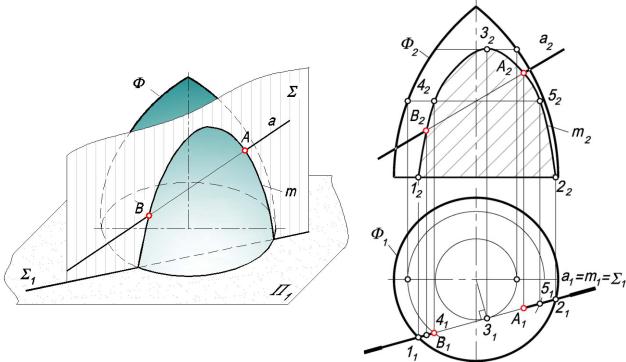
Точки пересечения прямой линии с поверхностью в общем случае определяют по следующей схеме (рис. 10.15):

1)через прямую линию а проводят вспомогательную секущую плоскость Σ;

2)строят линию т пересечения этой вспомогательной секущей плоскости Σ с поверхностью Ф;

3)находят точки {А, В} пересечения прямой линии а с линией пересечения т поверхности вспомогательной плоскостью.

На рис. 10.16 по этой схеме решена задача на пересечение прямой а с поверхностью вращения Ф. На первом этапе через прямую а проводят горизонтально проецирующую плоскость Σ. Плоскость Σ пересекает поверхность Ф по линии т. Точки {А, В}= т ∩ а – искомые.

Для решения задачи часто используют проецирующие плоскости. Но в некоторых случаях для удобства решения задачи целесообразно заключать прямую не в проецирующую плоскость, а в плоскость общего положения, если такая плоскость позволяет получить более простую форму сечения.

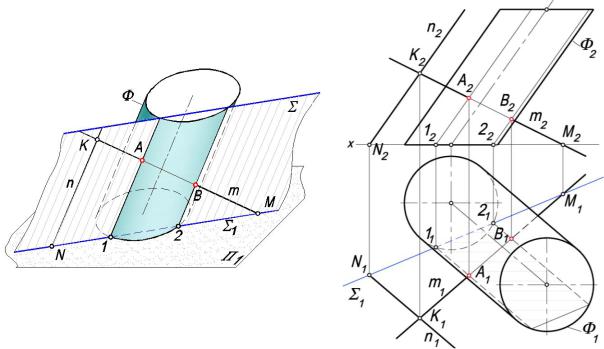
Задача 10.5.1. Найти точки пересечения цилиндрической поверхности и прямой линии m (рис. 10.17).

Рис. 10.17

Проведем через прямую т плоскость Σ, параллельную образующим цилиндрической поверхности, и построим горизонтальный след этой плоскости. Для этого на прямой т выберем произвольную точку К и через нее проведем прямую п, параллельную образующим цилиндра. Найдем горизонтальные следы прямых т и п – точки М (М1, М2) и N (N1, N2). Горизонтальный след плоскости Σ1 проходит через точки М1 и N1. Отметим точки 1 и 2 пересечения следа с основанием цилиндра. Через эти точки проходят образующие, пересекающие прямую т в точках А и В.

Задача 10.5.2. Определить точки пересечения прямой т с конической поверхностью (рис. 10.18).

Задача решается по общей схеме. Однако через прямую т проводим не проецирующую плоскость, а плоскость общего положения Σ, проходящую через вершину конуса S. Данная плоскость определяется прямой т и точкой S и пересекает конус по образующим.

Для нахождения этих образующих построим линию пересечения плоскости основания конуса и вспомогательной плоскости – горизонтальный след Σ1.

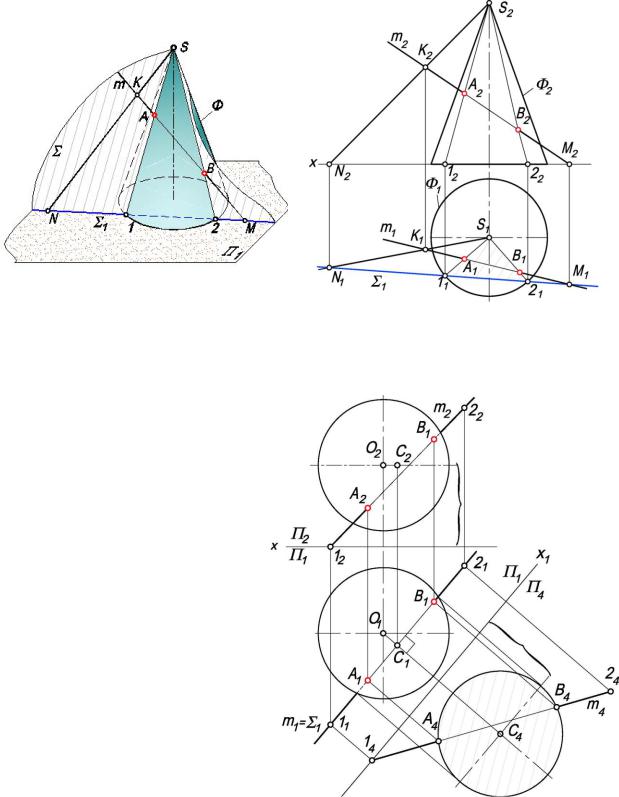
След Σ1 пересекает окружность основания в точках 1 и 2. Искомые образующие – линии (S-1) и (S-2). В пересечении этих линий и прямой т находим точки А и В - точки пересечения прямой т с поверхностью конуса.

Рис. 10.18

Задача 10.5.3. Найти точки пересечения сферической поверхности и линии т (рис. 10.19).

Прямую т, пересекающую сферу и имеющую общее положение относительно плоскостей проекций, заключим во вспомогательную горизонтально проецирующую плоскость Σ.

Введем новую плоскость проекций П4, параллельную плоскости Σ, на этой плоскости построим проекции прямой т4 и окружности, которая получится в пересечении сферы плоскостью Σ. На плоскости проекций П4 най-

10.6 Построение разверток поверхностей вращения

Для поверхностей вращения можно построить приближенную или условную развертку. Приближенную развертку можно построить для развертывающейся поверхности, условную – для неразвертывающейся.

При построении приближенной развертки заданную поверхность аппроксимируют поверхностями вписанных или описанных многогранников, имеющих грани в форме прямоугольников или треугольников. Поэтому при графическом выполнении развертки поверхности всегда приходится производить разгибание или спрямление прямых линий, принадлежащих поверхности, что неизбежно приводит к потере точности. Построение разверток многогранников рассмотрено ранее, поэтому ограничимся в рассмотрении примеров.

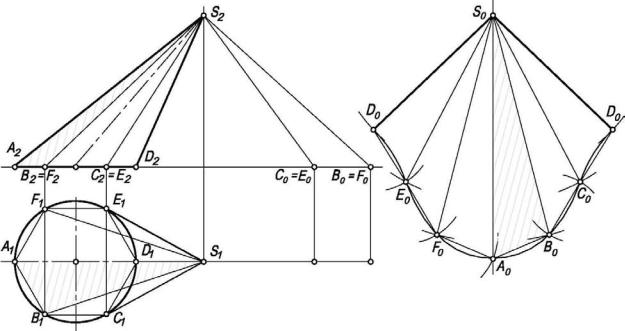
Задача 10.6.1. Построить развертку боковой поверхности наклонного конуса (рис. 10.20, а).

Рис. 10.20

Задача на построение развертки конической поверхности решается так же, как и в случае построения развертки боковой поверхности пирамиды, – способом треугольников. Для этого коническую поверхность аппроксимируют вписанной в нее пирамидальной поверхностью.

На рис. 10.20, б показана развертка поверхности пирамиды SABCDEF, вписанной в заданную коническую поверхность.

Фигуру S0D0E0F0A0B0C0D0 принимаем за приближенную развертку конической поверхности. Чем больше будет число граней у вписанной пирамиды, тем меньше будет разница между действительной и приближенной развертками конической поверхности.

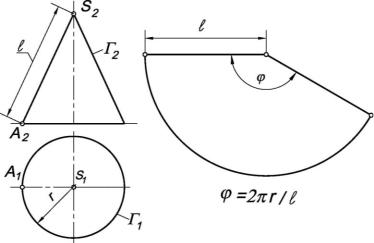
Развертка боковой поверхности прямого кругового конуса (рис. 10.21, а) представляет собой круговой сектор (рис. 10.21, б), радиус которого равен образующей конической поверхности ℓ = |AS|, а центральный угол φ определяется по формуле

ходится кроме изгибания осуществлять также сжатие и растяжение определенных участков листа.

Общий прием решения задачи на построение условной развертки состоит в том, что отсеки заданной поверхности аппроксимируют отсеками развертывающихся поверхностей – гранными, цилиндрическими или коническими.

Задача 10.6.2. Построить развертку цилиндроида, сопрягающего две трубы одинакового диаметра (рис. 10.22, а).

Решение сводится к следующему: заданную неразвертываемую поверхность цилиндроида аппроксимируем вписанными в нее отсеками конической поверхности, которые, в свою очередь, заменяем треугольниками.

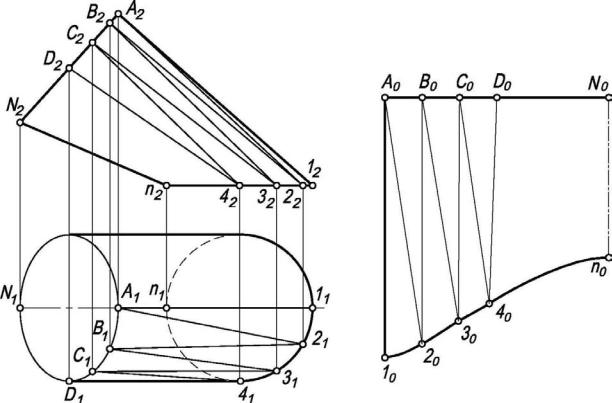
Чтобы заменить поверхность цилиндроида отсеками конических поверхностей, проводим на поверхности цилиндроида семейство прямолинейных образующих, параллельных плоскости параллелизма. В данном случае плоскостью параллелизма служит фронтальная плоскость проекций.

Рис. 10.22

На участке поверхности, заключенном между двумя смежными образующими (1-A) и (2-В,) проводим "диагональ" (2-А), полученные отсеки поверхности (1-A-2) и (А-2-В) принимаем за плоские треугольники. Так же поступаем и с остальными отсеками поверхности цилиндроида, заключенными между образующими. Для построения развертки необходимо найти натуральные величины сторон треугольников. После этого осуществляем построение развертки многогран-

рис. 10.20). Точки 10, 20,… и A0, B0,... соединим плавными кривыми. На рис. 10.22, б показана только половина развертки, а вторая половина симметрична ей относительно прямой N0n0.

10.7 Взаимное пересечение поверхностей

К числу важнейших задач в начертательной геометрии относятся так называемые обобщенные позиционные задачи. В краткой форме эти задачи могут быть сформулированы следующим образом:

построить линию пересечения поверхности с плоскостью; построить точки пересечения поверхности с прямой линией; построить линию взаимного пересечения поверхностей. Рассмотрим задачу о пересечении двух поверхностей, которая яв-

ляется некоторым обобщением уже известных нам позиционных задач.

Две поверхности пересекаются по некоторой линии, точки которой принадлежат каждой из пересекающихся поверхностей. Поэтому построение линии пересечения двух поверхностей Ф и Ψ сводится к нахождению общих точек, принадлежащих как множеству точек, составляющих поверхность Ф, так и другому множеству точек, входящих в состав поверхности Ψ.

Построение линии пересечения поверхностей осуществляется с помощью вспомогательных секущих поверхностей (посредников).

Сущность способа состоит в том, что заданные поверхности пересекают третьей, вспомогательной поверхностью и находят линии, по которым вспомогательная секущая поверхность пересекает каждую из заданных поверхностей. Вследствие принадлежности вспомогательной поверхности эти линии могут пересекаться, касаться или не иметь общих точек.

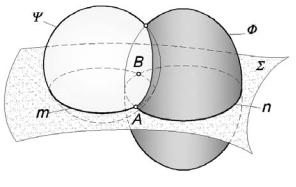
Если эти линии пересекаются (или касаются), то полученные точки пересечения (касания) принадлежат обеим данным поверхностям, а следовательно, и их линии пересечения (рис. 10.23):

Ф ∩ Σ = n; Ψ ∩ Σ = m;

m ∩ n ={A, B}.

Выполнив аналогичные операции n раз, получим множество точек, через которые

Вид и расположение вспомогательной секущей поверхности выбирают таким образом, чтобы в сечении получались графически простые линии – прямые, окружности. В качестве вспомогательных секущих поверхностей обычно выбираются плоскости или сферы. В первом случае построение осуществляется способом вспомогатель-

ных секущих плоскостей, а во втором – способом вспомогательных секущих сфер.

Прежде чем решить вопрос, какую вспомогательную секущую поверхность выбрать для построения линии пересечения поверхностей, необходимо выяснить, не занимает ли одна из пересекающихся поверхностей проецирующее положение. В этом случае решение поставленной задачи упрощается из-за того, что одна из проекций линии пересечения будет совпадать со следом проецирующей поверхности, которая входит в условие задачи. Решение сводится к определению недостающей проекции линии, принадлежащей поверхности, если известна одна ее проекция и указаны проекции поверхности.

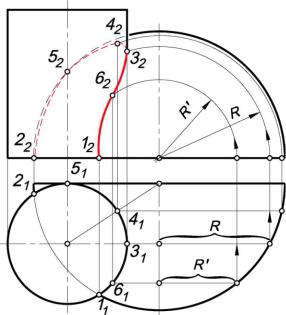
Задача. Построить линию пересечения цилиндрической и сферической поверхностей (рис. 10.24), причем цилиндрическая поверхность является горизонтально проецирующей.

Точки 1 и 2 расположены в основаниях поверхностей, точка 3 – крайняя правая на линии пересечения. Она является также границей видимости. Зная горизонтальную проекцию точки 31 на поверхности сферы, найдем ее фронтальную проекцию 32 с помощью окружности радиусом R. Точка 4 является наивысшей точкой линии пересечения, она ближайшая к вертикальной оси поверхности сферы, находится аналогичным способом. Точка 5 принадлежит главному меридиану сферы. Точки 1, 2, 3, 4, 5 яв-

ляются опорными (характерными) точками линии пересечения поверхностей. Для более точного построения искомой линии построим промежуточную точку 6.

10.8Построение линии пересечения поверхностей методом вспомогательных секущих плоскостей

При решении задач на построение линии пересечения поверхностей в качестве вспомогательных плоскостей выбирают проецирующие плоскости (часто плоскости уровня) или плоскости, вращающиеся вокруг прямой («пучок» плоскостей).

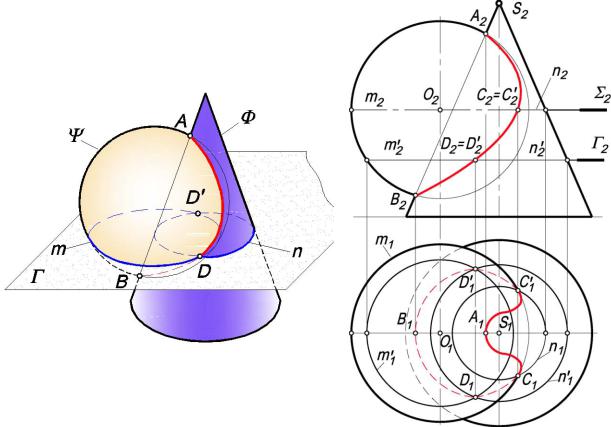
Задача 10.8.1. Построить линию пересечения конуса и сферы. Анализ условия показывает, что для решения могут быть исполь-

зованы горизонтальные плоскости уровня, пересекающие обе поверхности по окружностям (рис. 10.25, а). С помощью таких плоскостей можно построить любое количество произвольных точек.

Рис. 10.25

Определяем верхнюю А и нижнюю В опорные точки (на пересечении главных меридианов поверхностей). Эти точки устанавливают границы, в которых следует проводить вспомогательные секущие плоскости (рис. 10.25, б). Найдем точки С и С′ – точки пересечения экватора сферы с поверхностью конуса. Для этого проведем плоскость Σ, которая пересекает сферу по экватору m, конус – по парал-