
Kalashnikova_Nacher_geom
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Н.Г. Калашникова, Т.А. Татаренкова
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Рекомендовано редакционно-издательским советом ОрелГТУ в качестве учебного пособия для вузов
Орел 2010
УДК 514.18(075) ББК 22.151.3я7
К17
Рецензенты:
Кандидат технических наук, доцент кафедры «Инженерная графика и САПР»
Орловского государственного технического университета
Ю.П. Мельков
Доктор технических наук, профессор, заведующий кафедрой «Промышленное и гражданское строительство»
Курского государственного технического университета
С.И. Меркулов
Калашникова, Н.Г.
К17 Начертательная геометрия: учебное пособие для вузов / Н.Г. Калашникова, Т.А. Татаренкова. – 2-е изд. – Орел: Орел-
ГТУ, 2010. – 145 с.
В учебном пособии изложены основные теоретические положения классического курса начертательной геометрии в объеме, предусмотренном современными стандартами образования для технических специальностей. Пособие имеет своей целью помочь студентам в освоении теории и получении навыка решения задач. Приведено большое количество примеров решения задач с подробным описанием. Все разделы проиллюстрированы наглядными рисунками и чертежами, что облегчает восприятие материала.
Предназначено студентам технических специализаций и специальностей всех форм обучения, изучающим дисциплину «Начертательная геометрия».
УДК 514.18(075) ББК 22.151.3я7
© ОрелГТУ, 2010
СОДЕРЖАНИЕ
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ………………………………………….6
ВВЕДЕНИЕ………………………………………………………………9
1ОБРАЗОВАНИЕ ПРОЕКЦИЙ. ТОЧКА…………………………….10
1.1Методы проецирования………………………………………...10
1.2Центральное проецирование…………………………………...10
1.3Параллельное проецирование………………………………….11
1.4Инвариантные свойства параллельного проецирования……..12
1.5Проецирование точки на две плоскости проекций…………...14
1.6Проецирование точки на три плоскости проекций…………...17
2ЛИНИЯ………………………………………………………………...20
2.1Определение и задание линии на чертеже…………………….20
2.2Прямая. Положение прямой относительно плоскостей проекций…………………………………………………………20
2.3Прямые уровня…………………………………………………..21
2.4Проецирующие прямые…………………………………………23
2.5Принадлежность точки прямой………………………………...24
2.6Следы прямой…………………………………………………...25
2.7Определение длины отрезка прямой линии и углов его наклона к плоскостям проекций………………….26
2.8Взаимное положение двух прямых в пространстве…………..29
2.9Теорема о проецировании прямого угла………………………31
3ПЛОСКОСТЬ…………………………………………………………32
3.1Задание плоскости на чертеже…………………………………32
3.2Следы плоскости………………………………………………..33
3.3Положение плоскости относительно плоскостей
проекций………………………………………………………...34
3.3.1Проецирующие плоскости…………………………………..35
3.3.2Плоскости уровня……………………………………………38
3.4Прямая и точка в плоскости……………………………………39
3.5Прямые особого положения в плоскости……………………...40
3.6Построение проекций плоских фигур…………………………44 4 ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ, ПРЯМОЙ ЛИНИИ И ПЛОСКОСТИ………………………………….45
4.1Относительное положение двух плоскостей………………….45
4.2Относительное положение прямой линии и плоскости……...45
4.3Взаимная параллельность плоскостей…………………………45
4.4Взаимная параллельность прямой линии и плоскости……….46
4.5Пересечение прямой линии с проецирующей плоскостью…..47
4.6Пересечение плоскости общего положения
спроецирующей плоскостью…………………………………..48
4.7Пересечение прямой линии с плоскостью общего положения………………………………………………50
4.8Пересечение двух плоскостей общего положения……………52
5 ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ,
ПРЯМЫХ, ПЛОСКОСТЕЙ…………………………………………….56
5.1Взаимно перпендикулярные прямая и плоскость………….....56
5.2Взаимно перпендикулярные прямые…………………………..58
5.3Взаимно перпендикулярные плоскости……………………….60
6 СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИОННОГО ЧЕРТЕЖА. ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ………………...61
6.1Основные понятия и определения……………………………..61
6.2Замена плоскостей проекций…………………………………..62
6.3Замена одной плоскости проекций……………………………62
6.4Замена двух плоскостей проекций…………………………….63
6.5Основные задачи, решаемые способом замены плоскостей проекций…………………………………………...65
7 ПЕРЕМЕЩЕНИЕ (ВРАЩЕНИЕ) ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ В ПРОСТРАНСТВЕ………………………………………...70
7.1Основные понятия и определения……………………………..70
7.2Плоскопараллельное перемещение……………………………70
7.3Вращение вокруг оси, перпендикулярной к плоскости проекций………………………………………………………....73
7.4Вращение вокруг оси, параллельной плоскости проекций (вращение вокруг линии уровня)…………………...77
7.5Вращение вокруг оси, принадлежащей плоскости проекций (совмещение)………………………………………...82
8МНОГОГРАННИКИ…………………………………………………86
8.1Общие сведения о многогранниках……………………………86
8.2Чертежи многогранников………………………………………86
8.3Пересечение многогранника плоскостью……………………..87
8.4Пересечение многогранника прямой линией…………………91
8.5Взаимное пересечение многогранников………………………92
8.6Развертки многогранников……………………………………..93
9ПОВЕРХНОСТИ……………………………………………………...97
9.1Основные понятия и определения……………………………..97
9.2Линейчатые поверхности с одной направляющей…………..100
9.3Линейчатые поверхности с двумя направляющими
иплоскостью параллелизма…………………………………..102
9.4Линейчатые поверхности с тремя направляющими……...…104
9.5Нелинейчатые поверхности с образующей переменного вида……………………………………………...106
9.6Нелинейчатые поверхности с образующей постоянного вида………………………………………………106
9.7Винтовые поверхности………………………………………..107 10 ПОВЕРХНОСТИ ВРАЩЕНИЯ……………………………...……109
10.1Основные понятия и определения……………………….109
10.2Классификация поверхностей вращения………………...110
10.3Пересечение поверхности вращения плоскостью……….111 10.3.1 Пересечение цилиндра вращения плоскостью………..111 10.3.2 Пересечение конической поверхности плоскостью….113 10.3.3 Пересечение сферической поверхности плоскостью...116
10.4Касательная плоскость и нормаль к поверхности………117
10.5Пересечение прямой линии с поверхностью……………121
10.6Построение разверток поверхностей вращения…………124
10.7Взаимное пересечение поверхностей……………………127
10.8Построение линии пересечения поверхностей методом вспомогательных секущих плоскостей………..129
10.9Построение линии пересечения поверхностей методом вспомогательных секущих сфер……………….132
10.10Особые случаи построения линии пересечения поверхностей………………………………………………137
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ…………………………………….140
ЛИТЕРАТУРА…………………………………………………………144
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
1.Точки обозначают прописными буквами латинского алфавита: А, В, С,… или арабскими цифрами: 1, 2, 3…
2.Прямые и кривые линии, расположенные произвольно относительно плоскостей проекций, обозначают строчными буквами латинского алфавита: a, b, c, d, …, l, m, n…
Линии уровня: h - горизонталь, f – фронталь, p - профильная прямая.
Для описания линий принимают также следующие обозначения: (АВ) – прямая, определяемая точками А и В; [АВ) – луч с началом в точке А;
[АВ] – отрезок прямой, ограниченный точками А, В;АВ – длина отрезка, натуральная величина отрезка АВ; AB – вектор.
Если нет необходимости четко различать отрезок, прямую и т.д., скобки могут быть опущены.
3.Плоскости обозначают прописными буквами греческого алфа-
вита: , , , , , , , …
4.Пространственные фигуры, поверхности обозначают прописными буквами греческого алфавита: , .
5.Последовательность точек (или других элементов) отмечают соответствующими индексами: A , A , A ,…, a , a , a .
6.Несобственные элементы (точки, линии и т.д.) обозначают соответствующей буквой с верхним индексом ∞. Например: А , а ,…
7.Углы обозначаются строчными буквами греческого алфавита:, , , , , , а также символически: АВС – угол с вершиной в точке В; а^ – угол, составленный прямой а и плоскостью .
8.Плоскости проекций обозначаются греческой буквой П с до-
бавлением подстрочного индекса: П1 – горизонтальная, П2 – фронтальная, П3 – профильная и т.д.
9.Оси проекций: х – ось абсцисс; у – ось ординат; z – ось аппли-
кат.
10.Проекции точек, линий, фигур обозначают теми же буквами или цифрами, что и оригинал, с добавлением подстрочного индекса, соответствующего плоскости проекций:
на произвольную плоскость проекций П0 – А0, В0, С0, а0, b0, c0; на горизонтальную плоскость проекций П1 – А1, В1, С1, а1, b1, c1; на фронтальную плоскость проекций П2 – А2, В2, С2, а2, b2, c2; на профильную плоскость проекций П3 – А3, В3, С3, а3, b3, c3.
11. Теоретико-множественные символы, обозначающие основные геометрические операции:
{A,B,C,…} – множество с элементами A, B, C,…;
– принадлежность точки (элемента множества) геометрической фигуре (множеству): А m, B ;
– принадлежность (включение) геометрической фигуры (под-
множества) данной фигуре (множеству): m ; |
|
||||||
– |
объединение множеств: [АВ] [ВС] – ломаная АВС; |
||||||
– |
пересечение множеств а Σ; |
|
|
||||
= |
– |
геометрическое совпадение |
точек; результат операции: |
||||
А1 = В1; а Σ = А; |
|
|
|||||
|
– |
параллельность прямых, плоскостей: а b; Σ |
; |
||||
– перпендикулярность прямых, плоскостей: а |
; |
||||||
|
∙ |
– скрещивающиеся прямые: а ∙ |
b; |
|
|||
|
|
|
|
|
|
|
|
– отображение геометрических элементов: А А1; 12. Знаки, обозначающие логические операции:
– соответствует союзу «и»;– соответствует союзу «или»;
– логическое следование («если …, то…»): а b а1 b1 , а2 b2;– равносильные утверждения («в том и только в том случае, ес-
ли…»).
Приведенные символы могут быть перечеркнуты наклонной чертой, что соответствует частице «не». Например: А m – точка А не принадлежит линии m.
Латинский алфавит
A, a |
– |
а |
J, j |
– |
йот (жи) |
S, s |
– |
эс |
B, b |
– |
бе |
K, k |
– |
ка |
T, t |
– |
те |
C, c |
– |
це |
L, l |
– |
эль |
U, u |
– |
у |
D, d |
– |
де |
M, m |
– |
эм |
V, v |
– |
ве |
E, e |
– |
э |
N, n |
– |
эн |
W, w |
– |
дубль-ве |
F, f |
– |
эф |
O, o |
– |
о |
X, x |
– |
икс |
G, g |
– ге (же) |
P, p |
– |
пе |
Y, y |
– |
ипсилон |
|
H, h |
– ха (аш) |
Q, q |
– |
ку |
Z, z |
– |
зета |
|
I, i |
– |
и |
R, r |
– |
эр |
|
|
|
Греческий алфавит
|
– |
альфа |
|
– |
иота |
|
– |
ро |
|
– |
бета |
|
– |
каппа |
|
– |
сигма |
|
– |
гамма |
|
– |
ламбда |
|
– |
тау |
|
– |
дельта |
|
– |
ми |
|
– |
и псилон |
|
– |
э псилон |
|
– |
ни |
|
– |
фи |
|
– |
дзета |
|
– |
кси |
|
– |
хи |
|
– |
эта |
|
– |
о микрон |
|
– |
пси |
|
– |
тета |
|
– |
пи |
|
– |
о мега |
ВВЕДЕНИЕ
Пособие представляет краткое изложение классического курса начертательной геометрии. При подборе материала авторы старались включить в издание минимально необходимый объем информации, который позволяет на практике решать задачи по определению формы, размеров и взаимного расположения объектов, представленных на чертеже. При этом наиболее подробно были изложены разделы, вызывающие затруднение у студентов при самостоятельном изучении. Для более полного освоения курса начертательной геометрии следует воспользоваться перечисленными в библиографическом списке учебниками, задачниками и справочными пособиями.
Данное пособие может быть использовано как в качестве дополнения к курсу лекций, так и для организации самостоятельной работы студентов.
В число дисциплин, составляющих основу инженерного образования, входит начертательная геометрия, которая изучает теоретические основы методов построения изображений (чертежей) пространственных фигур на плоскости и способы решения на этих чертежах различных геометрических задач.
Предметом начертательной геометрии является разработка об-
щих методов построения и чтения чертежей, не зависящих от технологии производства и служебного назначения документов, а также способов решения на чертежах геометрических задач, связанных с геометрическими свойствами формы изображаемых предметов. Объекты, различаемые только по их форме и размерам, принято называть
геометрическими фигурами.
Начертательная геометрия учит:
строить чертежи геометрических фигур;
читать чертежи;
решать на чертежах задачи по определению натуральных величин (размеров) изображаемых элементов;
решать на чертежах задачи на взаимное расположение геометрических фигур.
Кроме того, начертательная геометрия является лучшим средством развития пространственного мышления, без которого немыслимо никакое инженерное творчество.
1 ОБРАЗОВАНИЕ ПРОЕКЦИЙ. ТОЧКА
1.1Методы проецирования
Не всякое изображение предмета на листе бумаги позволяет точно определить геометрическую форму предмета. Закономерное изображение пространственного предмета достигается при помощи метода проецирования. Получающийся при этом чертеж называется проекци-
онным.
С позиции теории множеств любую геометрическую фигуру следует рассматривать как множество всех принадлежащих ей точек. Отображение геометрической фигуры на плоскость (или какую-либо другую поверхность) можно получить путем проецирования ее точек на эту плоскость (поверхность). Таким образом, построение проекций пространственного предмета сводится к построению проекций некоторого множества его точек. Поэтому изучение метода проецирования начинают с построения проекции точки.
1.2Центральное проецирование
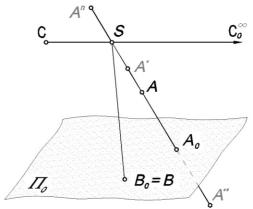
Зададим в пространстве некоторую плоскость П0, называемую
плоскостью проекций, и произвольную точку S – центр проецирова-
ния, не принадлежащую плоскости П0 (рис. 1.1).
П0 – произвольная плоскость проекций;
S – центр проекций;
SA – проецирующая прямая;
А0 – центральная проекция точки А на плоскость П0
Рис. 1.1
