- •Глава I. Производная и ее приложения. § 1. Формулы дифференцирования.
- •1.1. Справочный материал.
- •1.2. Таблица производных элементарных функций.
- •1.7. Производная сложной функции.
- •Задачи раздела I.
- •Задачи раздела II.
- •Решение задач раздела I.
- •Ответы к задачам раздела II.
- •§ 2. Исследование функции на монотонность.
- •2.1 Справочной материал.
- •2.2. Схема исследования функции на монотонность.
- •Ответ: убывает на (-; 2),
- •Ответ: возрастает на промежутке ; убывает на промежутке . § 3. Исследование функции на экстремум.
- •3.1. Справочный материал.
- •3.2 Схема исследования функции на экстремум.
- •Ответ: экстремум не существует.
- •§ 4. Наибольшее и наименьшее значения непрерывной функции на отрезке.
- •4.1. Справочный материал.
- •4.2 Схема нахождения наибольшего и наименьшего значений функции .
- •Ответ: 8 м и 16 м. Задачи раздела I.
- •Задачи раздела II.
- •Решение задач раздела I.
- •Ответ: .
- •Ответ: возрастает для всех хr.
- •Убывает на (-7/3; 1)
- •Ответ: возрастает на (0; 3), убывает на (3; 6).
- •Ответ: экстремумов нет.
- •11. Квадрат со стороной 9.
Глава I. Производная и ее приложения. § 1. Формулы дифференцирования.
1.1. Справочный материал.
Пусть функция
y=f(x)
определена на промежутке Х.
Если аргумент изменяется от фиксированного
значения х
до нового значения
![]()
![]() ,
то значение функции изменяется от
,
то значение функции изменяется от![]() до
до![]() .
.
Определение 1.1. Дифференциальным отношением называется отношение приращения функции к приращению аргумента
![]()
Определение 1.2. Дифференциальное отношение измеряет среднюю скорость изменения функции y=f(x).
Определение 1.3.
Производной
функции
y=f(x)
в некоторой точке x
называется предел отношения приращения
функции к приращению аргумента при
![]() (если этот предел существует)
(если этот предел существует)
![]()
Определение 1.4. Процесс нахождения производной называется дифференцированием.
Производную обозначают символами
![]()
1.2. Таблица производных элементарных функций.
Пример 1.1. Вычислить производные:
по формулам
![]()
![]() где
где![]()
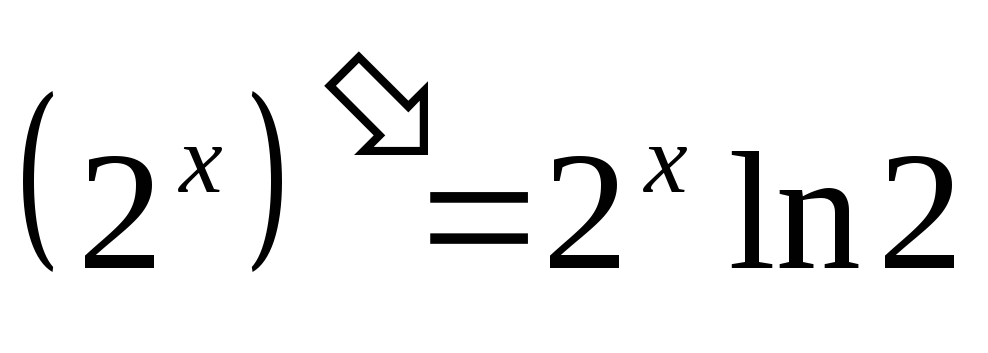 (по формуле
(по формуле
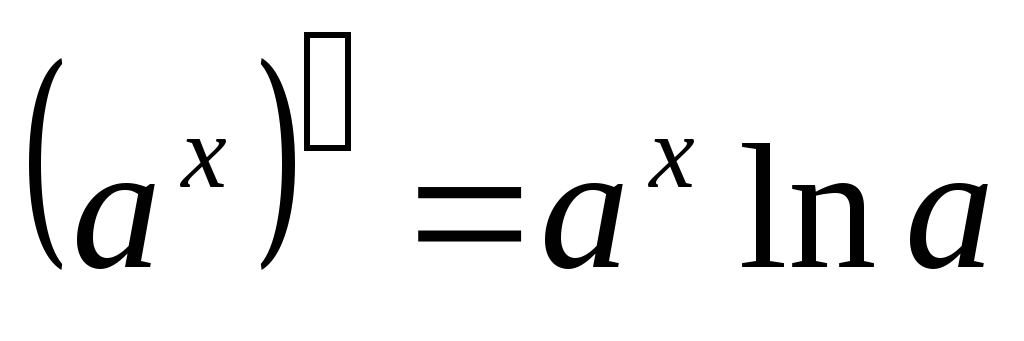 ,
гдеa=2)
,
гдеa=2)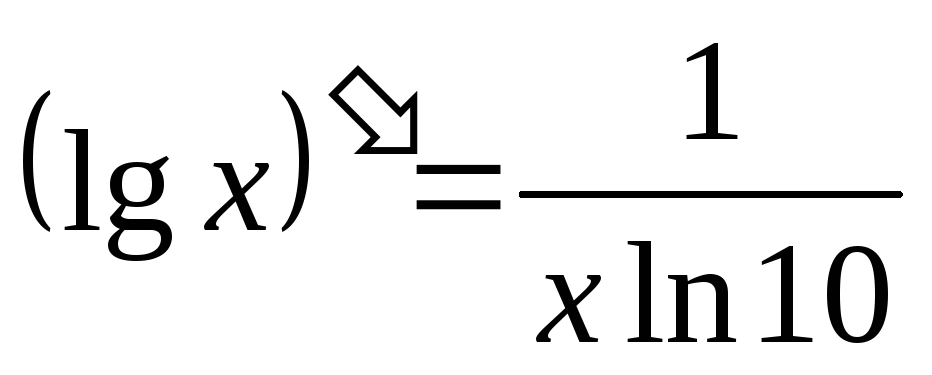 (по формуле
(по формуле
 ,
гдеa=10)
,
гдеa=10)
1.3. Производная суммы.
Определение 1.5.Производная суммы двух дифференцируемых в точке x функций u(x) и v(x) существует в этой точке и вычисляется по формуле:
![]()
или короче
![]() (1)
(1)
Пример 1.2. Вычислить производные:
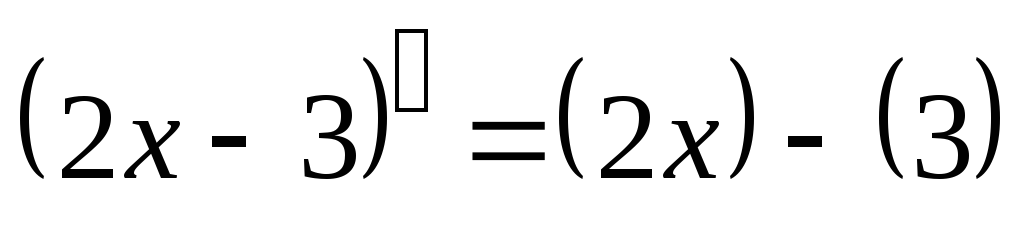 =2-0=2
(по формулам
=2-0=2
(по формулам
 ,
,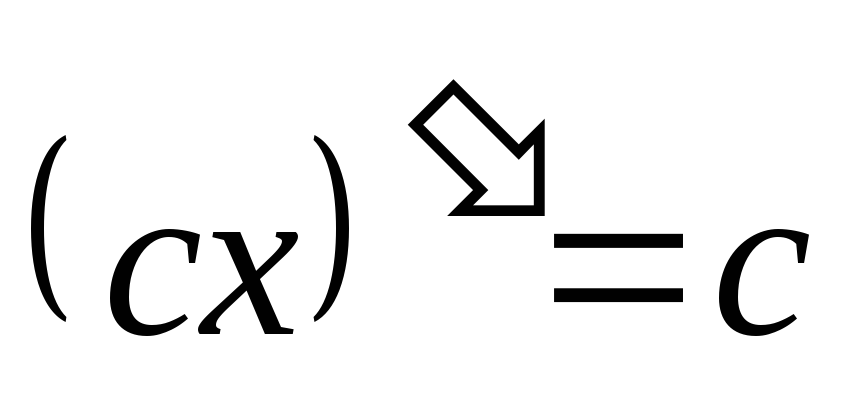 ,
,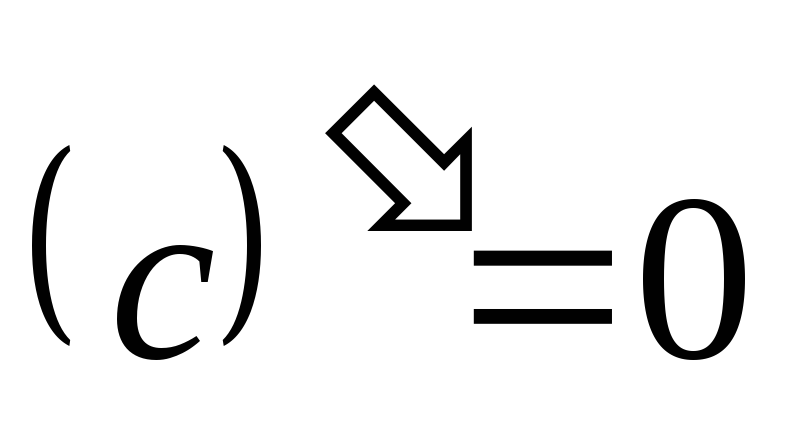 )
)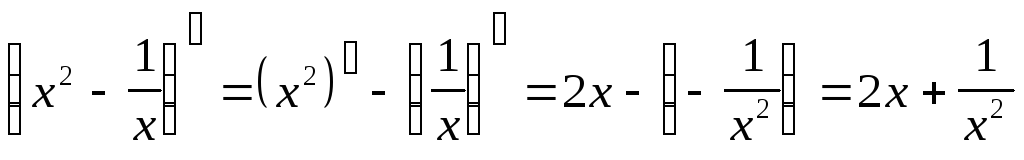
(по формулам
![]() ,
,![]() ,
,![]() )
)
1.4. Производная произведения.
Определение 1.6.Производная произведения двух дифференцируемых в точке x функций u(x) и v(x) существует в этой точке и вычисляется по формуле:
![]()
или короче
![]() (2)
(2)
Утверждение 1.1 Если функция u=u(x) дифференцируема в точке х, а С – постоянная, то функция Cu дифференцируема в этой точке и
![]() (3)
(3)
или короче: постоянный множитель можно выносить за знак производной.
Доказательство самостоятельно
Пример 3.
Найти
![]() :
:![]() .
.
Решение.
![]()
![]() .
.
Была использована
формула 4:
![]()
1.5. Производная частного.
Определение 1.6 Производная частного двух дифференцируемых в точке x функций u(x) и v(x) при условии, что функция v(x) не равна нулю в этой точке, существует в этой точке и вычисляется по формуле:
![]()
или короче
![]() (4)
(4)
Пример 4.
Найти значение производной функции
![]() в точкех
= 1:
в точкех
= 1:
Решение.
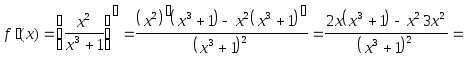
![]()
![]()
Ответ:
![]()
1.6. Понятие сложной функции.
Пример 5.
Пусть требуется вычислить значение
функции
![]() в некоторой фиксированной точкеx.
Для этого нужно:
в некоторой фиксированной точкеx.
Для этого нужно:
1) вычислить
![]() ;
;
найти значение синуса при полученном значении
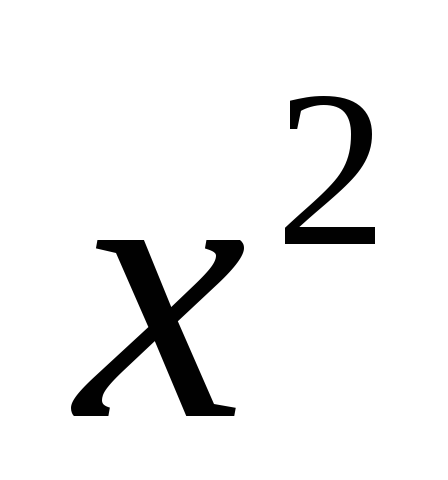 .
.
Иными словами,
сначала надо найти значение функции
![]() ,
а затем
,
а затем![]() ,
аргументu
( u
=g(x))
в этом случае
называют промежуточным, а x
– независимой переменной.
,
аргументu
( u
=g(x))
в этом случае
называют промежуточным, а x
– независимой переменной.
Пусть функция u=g(x) определена на некотором множестве X, а функция y=f(u) – на множестве значений функции u=g(x), тогда на множестве X определена функция y=f(g(x)), называемая сложной функцией.
Пример 6.
Рассмотрим функцию
![]() .
Чтобы найти значение этой функции в
фиксированной точкех,
нужно сначала найти значение функции
g(x)
= 1 - x2,
а потом найти значение
.
Чтобы найти значение этой функции в
фиксированной точкех,
нужно сначала найти значение функции
g(x)
= 1 - x2,
а потом найти значение
![]() .
В этом примере
.
В этом примере![]() ,
гдеu
= 1 - x2.
,
гдеu
= 1 - x2.
Пример 7.
Составить сложную функцию
![]() ,
если
,
если![]() .
.
Решение.
![]() .
.
1.7. Производная сложной функции.
Если функция u=g(x) дифференцируема в точке x, а функция y=f(u) дифференцируема в точке u=g(x), то сложная функция y=f(g(x)), дифференцируема в точке x, причем:
![]()
Короче эту формулу записывают в виде:
![]()
Пример 8. Найти производные функций
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
Решение.
а) Здесь
![]()
Значит
![]()
Решение.
б) Так как
![]() то
то![]() .
.
Решение.
в)
![]() .
.
Решение. г)
![]()
Решение. д)
![]() .
.
Пример 9. Найти производные функций
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
ж)
![]()
Решение.
а)
![]()
![]()
Решение.
б)
![]()
![]()
Решение. в) Прежде, чем дифференцировать функцию, целесообразно упростить ее варажение, применяя формулы логарифмирования:
![]() .
Теперь
.
Теперь
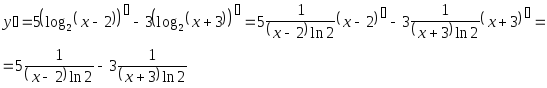
Решение.
г)
![]() .
.
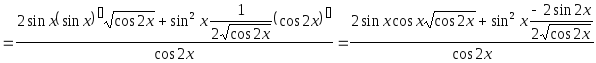
После преобразований. получим:
![]()
![]()
![]()
Решение.
д)
![]()
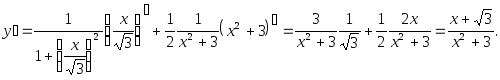
Решение. е) По правилу дифференцирования сложной функции
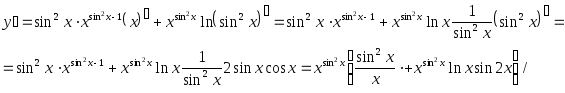
Решение. ж) При дифференцировании неявно заданной функции учитываем, что y есть функция от x:
![]() откуда
откуда
![]()