
- •Содержание
- •Пояснительная записка
- •1. Интегральное исчисление функций одной независимой переменной
- •1.1. Неопределенный интеграл
- •Свойства неопределенного интеграла (правила интегрирования)
- •4. Интегрирование простейших рациональных дробей.
- •6. Интегрирование тригонометрических функций.
- •7. Интегрирование иррациональных функций.
- •1.2. Определенный интеграл Основные свойства определенного интеграла
- •Правила вычисления определенных интегралов
- •1.3. Приложение определенного интеграла
- •Вычисление площади плоской фигуры
- •Вычисление длины дуги плоской кривой
- •2. Дифференциальное исчисление функций нескольких переменных
- •3. Дифференциальные уравнения
- •1. Уравнения с разделяющимися переменными
- •2. Однородные уравнения
- •3. Линейные уравнения первого порядка
- •4. Уравнение Бернулли
- •Сводная таблица видов частных решений для различных видов правых частей
- •Контрольная работа №4. «Интегральное исчисление функции одной независимой переменной»
- •Контрольная работа №5. «Дифференциальное исчисление функций многих переменных»
- •Контрольная работа №6. «Дифференциальные уравнения»
- •Список литературы
6. Интегрирование тригонометрических функций.
Интегралы
вида
![]() ,
где
,
где![]() - рациональная функция.
Интегралы указанного вида приводят к
интегралам от рациональных функций с
помощью, так называемой универсальной
тригонометрической подстановки
- рациональная функция.
Интегралы указанного вида приводят к
интегралам от рациональных функций с
помощью, так называемой универсальной
тригонометрической подстановки
![]() .
В результате этой подстановки имеем:
.
В результате этой подстановки имеем:
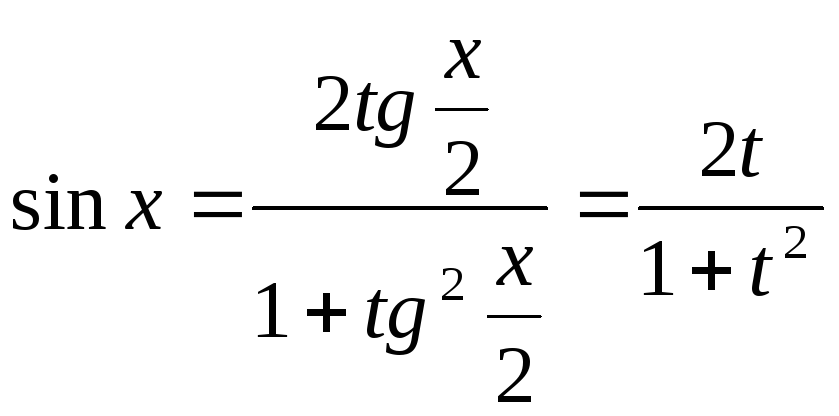 ,
,
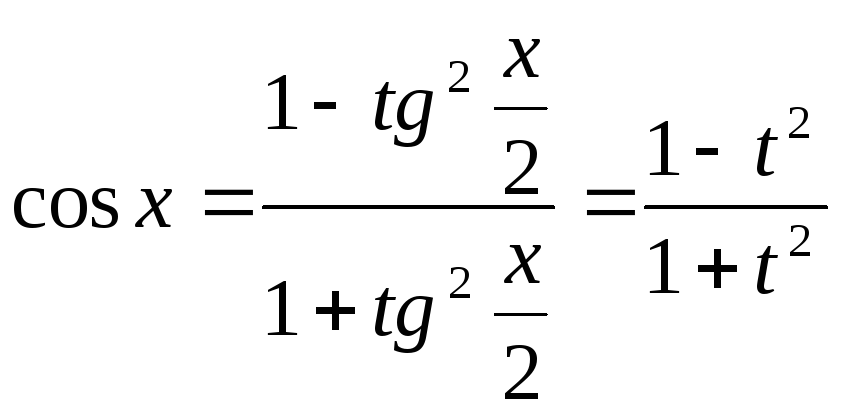 ,
,
![]() ,
,![]() .
.
Пример
1.18. Вычислить
![]() .
.
Решение.
Подынтегральная
функция является рациональной относительно
![]() и
и![]() .
Воспользуемся подстановкой
.
Воспользуемся подстановкой![]() ,
тогда
,
тогда![]() ,
,
![]() ,
,
![]() ,
откуда
,
откуда
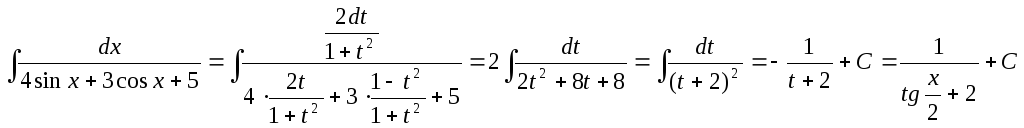
Замечание
1.3. Универсальная
подстановка
![]() во
многих случаях приводит к сложным
вычислениям.
во
многих случаях приводит к сложным
вычислениям.
В
некоторых частных случаях нахождение
интегралов вида
![]() можно
упростить.
можно
упростить.
1.
Если
![]() -нечетная
относительно
-нечетная
относительно
![]() ,
то есть, если
,
то есть, если![]() ,
то интеграл рационализируется подстановкой
,
то интеграл рационализируется подстановкой![]() .
.
2.
Если
![]() -нечетная
относительно
-нечетная
относительно
![]() ,
то есть, если
,
то есть, если![]() ,
то интеграл рационализируется подстановкой
,
то интеграл рационализируется подстановкой![]() .
.
3.
Если
![]() -четная
относительно
-четная
относительно
![]() и
и![]() ,
то есть
,
то есть![]() ,
то интеграл рационализируется подстановкой
,
то интеграл рационализируется подстановкой![]() (или
(или
![]() ).
).
Пример
1.19. Вычислить
![]() .
.
Решение.
Подынтегральная
функция четна относительно синуса и
косинуса. Полагаем
![]() ,
тогда
,
тогда
![]() ,
,![]() ,
,![]() ,
,![]() .
Отсюда получаем
.
Отсюда получаем
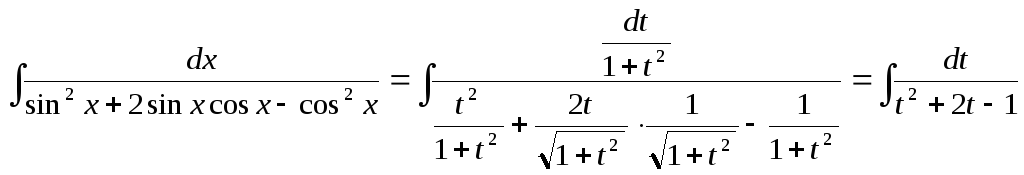 .
.
Далее имеем
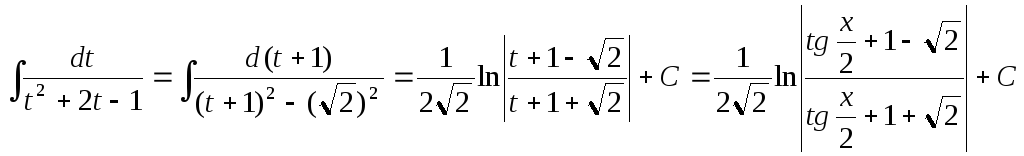 .
.
Заметим,
что нахождение интеграла можно упростить,
если в исходном интеграле разделить
числитель и знаменатель на
![]() :
:
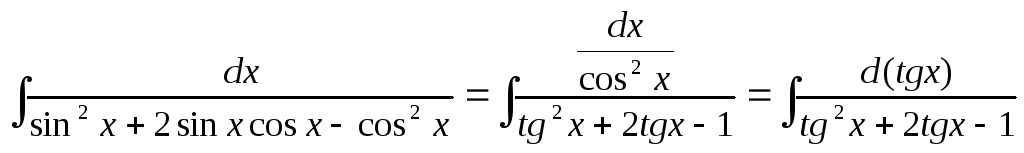 .
.
Интегралы
вида
![]() .
Выделим здесь два случая.
.
Выделим здесь два случая.
Случай
1. По
крайней мере один из показателей
![]() или
или![]() - нечетное положительное число.
- нечетное положительное число.
Если
![]() - нечетное положительное число, то
применяют подстановку
- нечетное положительное число, то
применяют подстановку![]() ;
если же
;
если же![]() - нечетное положительное число, то
применяют подстановку
- нечетное положительное число, то
применяют подстановку![]() .
.
Пример
1.20. Вычислить
![]() .
.
Решение.
Полагая
![]() ,
,![]() ,
получим
,
получим
![]()
![]() .
.
Случай
2. Оба
показателя
![]() или
или![]() - четные положительные числа. Здесь
следует преобразовать подынтегральную
функцию с помощью формул
- четные положительные числа. Здесь
следует преобразовать подынтегральную
функцию с помощью формул
|
|
(1.4) |
|
|
(1.5) |
|
| |
Пример
1.21. Вычислить
![]() .
.
Решение. Из формулы (1.4) следует, что
![]() .
.
Применив теперь формулу (1.5), получим
![]() .
.
Итак,
![]() .
.
7. Интегрирование иррациональных функций.
Интегралы
вида
![]() ,
где
,
где![]() - рациональная функция;
- рациональная функция;![]() - целые числа.С
помощью подстановки
- целые числа.С
помощью подстановки
![]() ,
где
,
где![]() - наименьшее общее кратное чисел
- наименьшее общее кратное чисел![]() ,
заданный интеграл преобразуется в
интеграл от рациональной функции.
,
заданный интеграл преобразуется в
интеграл от рациональной функции.
Пример
1.22. Вычислить
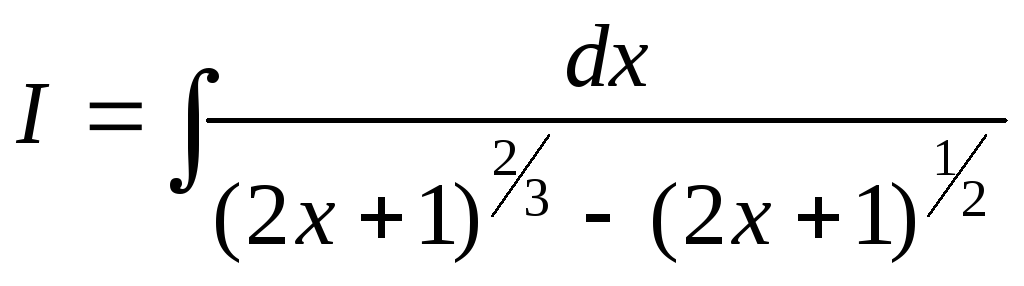 .
.
Решение.
Здесь
![]() поэтому
поэтому![]() .
Воспользуемся подстановкой
.
Воспользуемся подстановкой![]() ,
тогда
,
тогда![]() ,
,![]() и, следовательно,
и, следовательно,
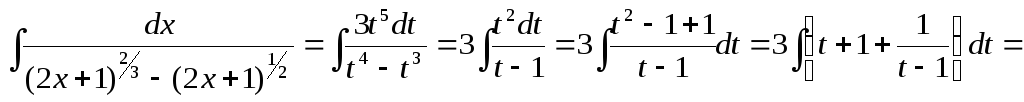
![]() .
.
Интегралы
вида
![]() ,
,
![]() ,
,![]() приводят
к интегралам от
приводят
к интегралам от
![]() ,
,![]() функции с помощью соответствующей
замены: для первого интеграла
функции с помощью соответствующей
замены: для первого интеграла![]() (или
(или![]() ),
для второго
),
для второго![]() (или
(или![]() )
и для третьего
)
и для третьего![]() (или
(или![]() ).
).
Пример
1.23. Вычислить
![]() .
.
Решение.
Положим
![]() ,
,![]() ,
,![]() .
Подставляя в исходный интеграл, получим
.
Подставляя в исходный интеграл, получим
![]() .
.
Выразим
![]() ,
если
,
если![]() ,
,
![]() .
.
Окончательно получаем
![]() .
.
1.2. Определенный интеграл Основные свойства определенного интеграла
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() ,
где
,
где![]() - постоянная.
- постоянная.
Правила вычисления определенных интегралов
1. Формула Ньютона-Лейбница:
![]() ,
,
где
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
,![]() - первообразная для
- первообразная для![]() .
.
2. Интегрирование по частям:
![]() ,
,
где
![]() ,
,![]() - непрерывно дифференцируемые функции
на отрезке
- непрерывно дифференцируемые функции
на отрезке![]() .
.
3. Замена переменной:
![]() ,
,
где
![]() - непрерывная вместе со своей производной
- непрерывная вместе со своей производной![]() на отрезке
на отрезке![]() ,
,![]() ,
,![]() ,
,![]() - функция, непрерывная на
- функция, непрерывная на![]() .
.
3.
Если
![]() - нечетная функция, то есть
- нечетная функция, то есть![]() ,
то
,
то
![]() .
.
4.
Если
![]() - четная функция, то есть
- четная функция, то есть![]() ,
то
,
то
![]() .
.
Пример
1.24. Вычислить
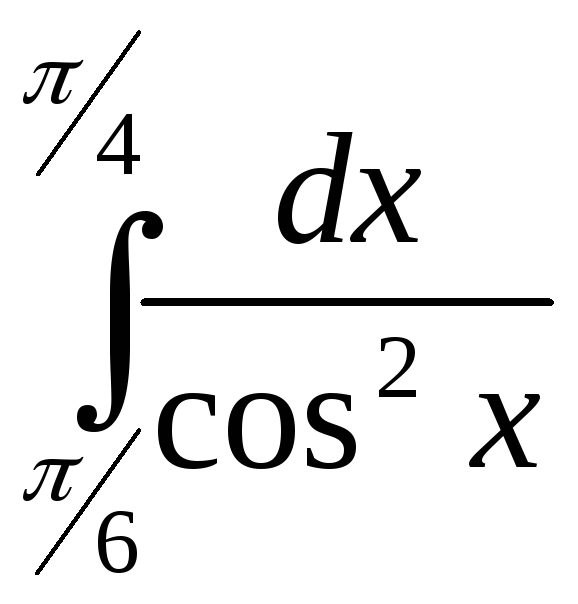 .
.
Решение. По формуле Ньютона-Лейбница имеем
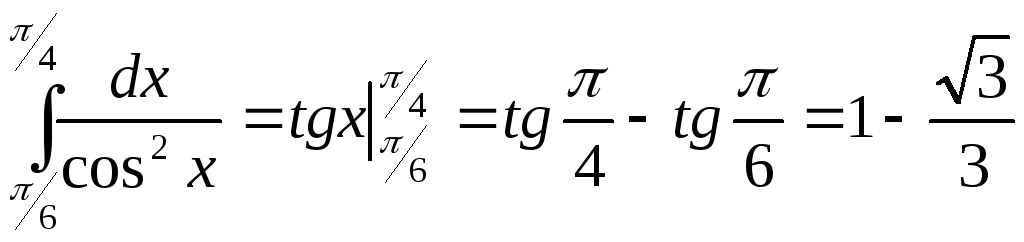 .
.
Пример
1.25. Вычислить
![]() .
.
Решение.
Воспользуемся
методом интегрирования по частям.
Положим
![]() ,
,![]() ,
откуда
,
откуда![]() ,
,![]() .
Тогда получим
.
Тогда получим
![]() .
.
Пример
1.26. Вычислить
![]() .
.
Решение.
Положим
![]() ,
тогда
,
тогда![]() ;
если
;
если![]() ,
то
,
то![]() ;
если
;
если![]() ,
тогда
,
тогда![]() .
Следовательно,
.
Следовательно,
![]() .
.
