§ 8.3. Прямые и плоскости в аффинном пространстве
Пример 1. Найдите проекцию прямой
на
плоскость
.
Решение. Прямая задана пересечением двух плоскостей. Найдем ее параметрическое уравнение, для чего решим систему уравнений.
.
Отсюда
,y
– свободная переменная,
и параметрическое уравнение данной
прямой
Отыщем точку пересечения А прямой с плоскостью:
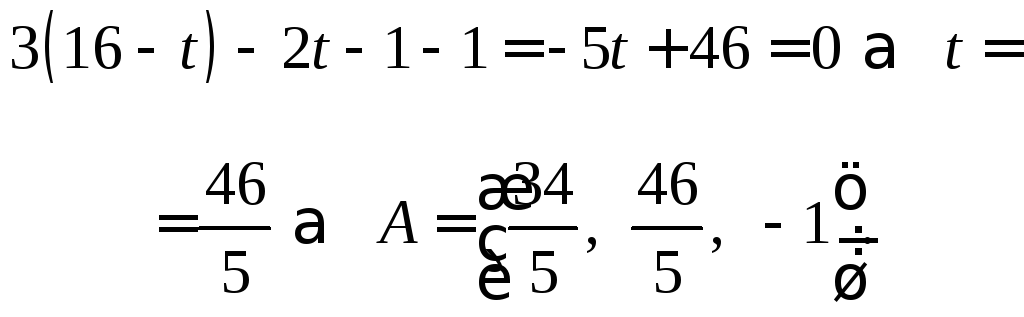
Выберем
на прямой
точку (0, 16, –1) и через нее проведем прямую
ортогональную плоскости
.
Получим точку пересеченияВ
этой прямой с плоскостью:
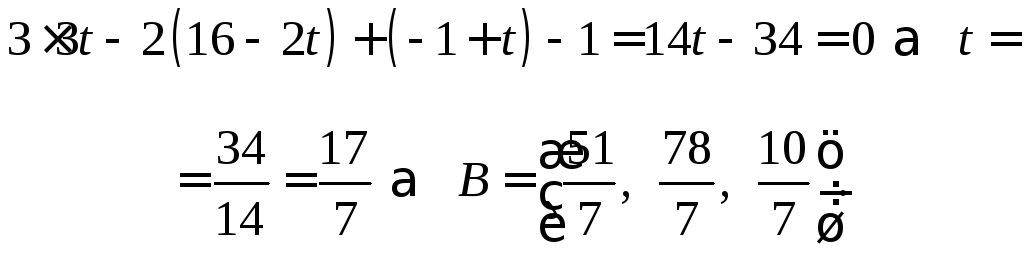
Проведем через точки А и В прямую. Поскольку
,
каноническое
уравнение искомой прямой
.
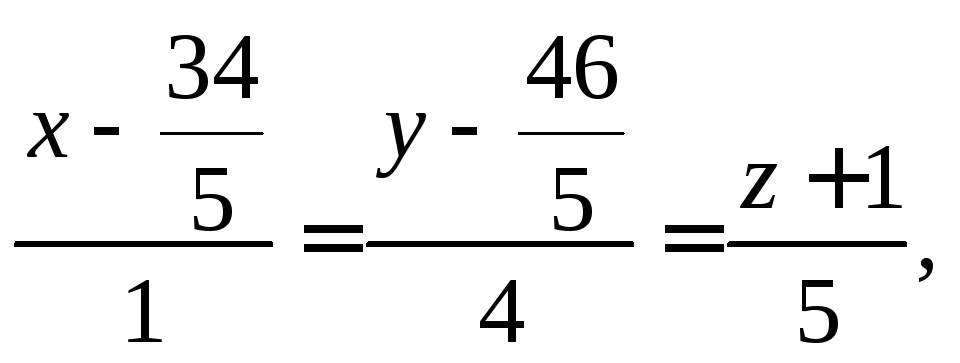
Пример
2. Найдите
точку, симметричную точке А
= (0, 5, –3) относительно прямой
Решение. Как и в предыдущем примере, прямая задана пересечением двух плоскостей. Найдем ее параметрическое уравнение:
Отсюда
свободная переменная,
и параметрическое уравнение данной
прямой
Определим
основание В перпендикуляра, опущенного
из точки А
на эту прямую. Предположим, что система
координат прямоугольная. Поскольку
и точкаВ
находится на минимальном расстоянии
от точки А,
найдем значение переменной t,
при котором
принимает свое наименьшее значение. В
силу того, что
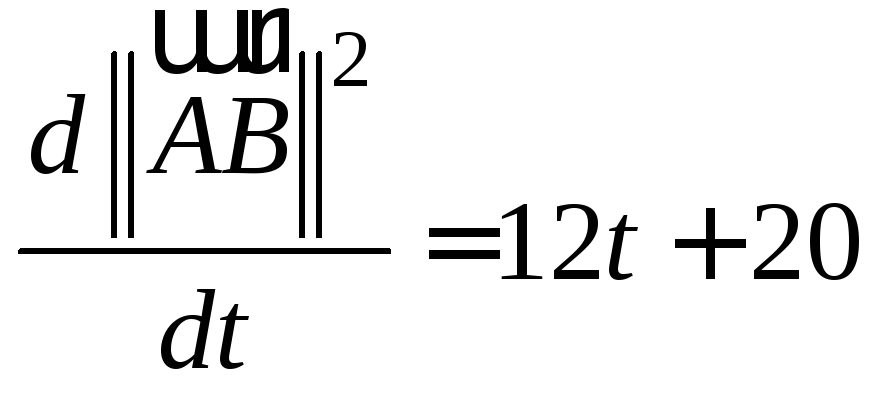и
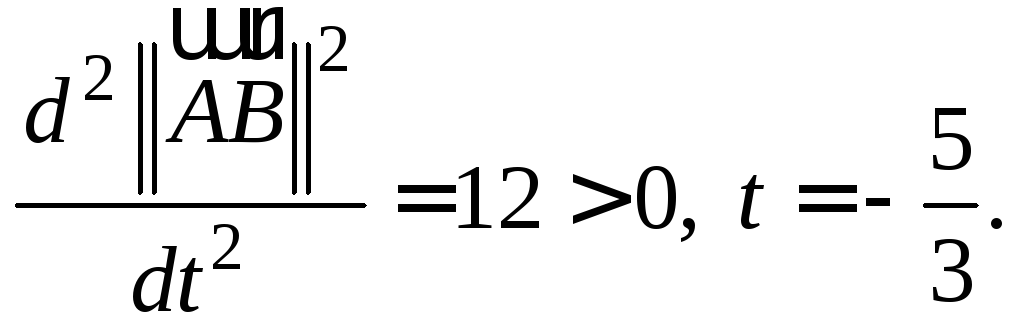
Следовательно,
и
параметрическое уравнение прямой АВ
Искомая
точка С
принадлежит прямой АВ
и отстоит от прямой
на расстояние
.
Найдем координаты точкиС
при помощи соотношения (8.1.8), в котором
.
Получим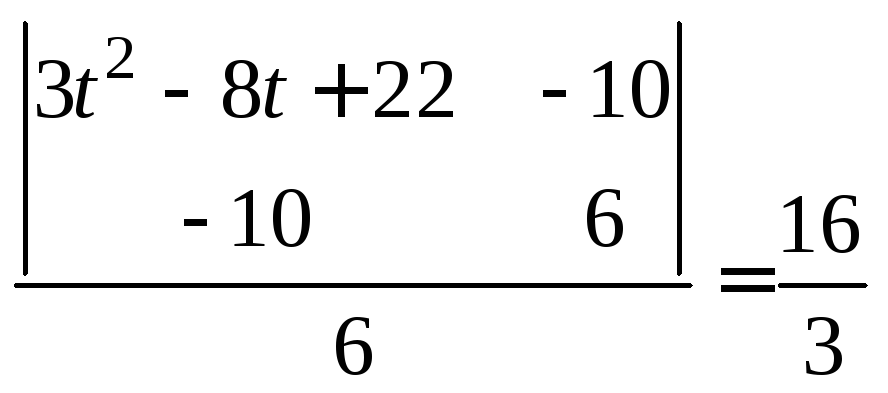
или
.
Данное
уравнение имеет два корня:
соответствует
точкеА,
– точкеС.
Таким образом,
.
Пример
3.
Составьте уравнение плоскости, проходящей
через прямую
параллельно прямой
.
Решение.
Воспользуемся формулой (8.2.6). Выбрав в
качестве
получим
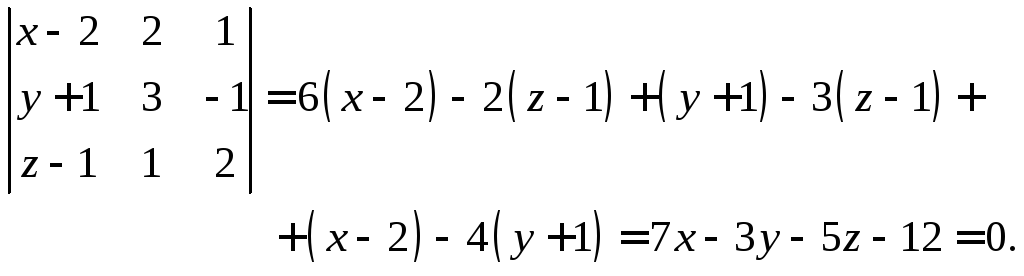
В задачах, требующих вычисления скалярных произведений, предполагается, что система координат прямоугольная.
8.3.1.
Проверьте, лежит ли данная прямая в
плоскости
,
параллельна этой плоскости или пересекает
ее в единственной точке; в последнем
случае найдите координаты точки
пересечения. Прямая задана уравнениями:
а)
;
б)
в)
8.3.2.
При каких а
прямая
а)
пересекает плоскость
б) параллельна этой плоскости;
в) лежит в этой плоскости.
8.3.3. Составьте уравнение плоскости, проходящей через прямую
параллельно
вектору
.
8.3.4. Найдите уравнение плоскости, проходящей через две параллельные прямые
и
.
8.3.5.
Составьте уравнение плоскости, проходящей
через точку
и параллельной прямым
и
8.3.6.
Составьте уравнение плоскости, проходящей
через прямую
и параллельной прямой
.
8.3.7.
Составьте уравнение плоскости, проходящей
через точку
и прямую, заданную уравнениями:
а)
;
б)
8.3.8.
Найдите проекцию точки
на прямую
8.3.9.
Составьте параметрическое уравнение
прямой, проходящей через точку
перпендикулярно плоскости
.
8.3.10.
Составьте уравнение прямой, проходящей
через точку
и перпендикулярной плоскости
.
8.3.11. Составьте
уравнение плоскости, проходящей через
точку
и перпендикулярной прямой
а)
;
б)
8.3.12.
Составьте уравнение плоскости, проходящей
через точку
и перпендикулярной двум плоскостям
и
.
8.3.13.
Составьте уравнение прямой, проходящей
через точку
перпендикулярно вектору
и пересекающей прямую
8.3.14.
Найдите уравнение прямой, проходящей
через точку
и пересекающей две прямые
и
8.3.15. Точка А лежит на прямой
.
Расстояние
от точки А
до плоскости
равно
.
Найдите координаты точкиА.
8.3.16. Составьте
уравнение прямой, симметричной прямой
относительно плоскости
.
8.3.17. Составьте
уравнения проекций на плоскость
следующих прямых:
а)
;
б)
в)
.
8.3.18.
Найдите угол между плоскостью
и прямой:
а)
;
б)
.
8.3.19.
Найдите точку, симметричную точке
относительно плоскости, проходящей
через прямые:
и
8.3.20. Точка А лежит на прямой
Расстояние
от точки А
до прямой
равно
.
Найдите координаты точкиА.