§ 8.5. Поверхности второго порядка

Геометрическое место точек трехмерного пространства, координаты которых в некоторой прямоугольной системе координат удовлетворяют уравнению

(8.5.1)

где хотя бы один из коэффициентов не равен нулю, называетсяповерхностью второго порядка.

Для любой поверхности второго порядка существует прямоугольная система координат , в которой уравнение этой поверхности имеет один из следующих 17 видов:

1) эллипсоид (рис. 8.4);

2) мнимый эллипсоид ;

3) однополостный гиперболоид (рис. 8.5);

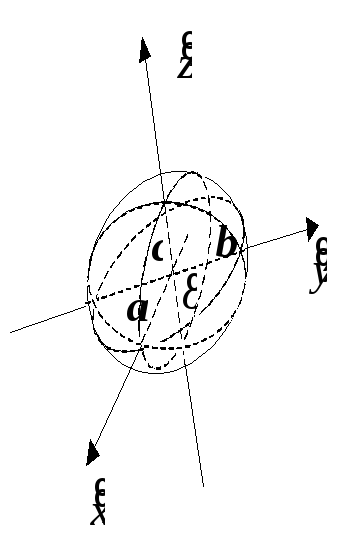
Рис. 8.4 Рис. 8.5

4) двуполостный гиперболоид (рис. 8.6);

5) конус (рис. 8.7);

6) мнимый конус ;

7) эллиптический параболоид (рис. 8.8);

8) гиперболический параболоид (рис. 8.9);

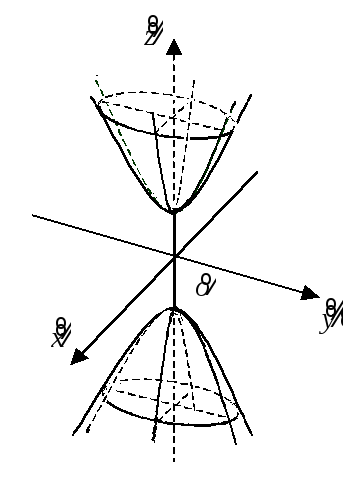
Рис. 8.6 Рис. 8.7

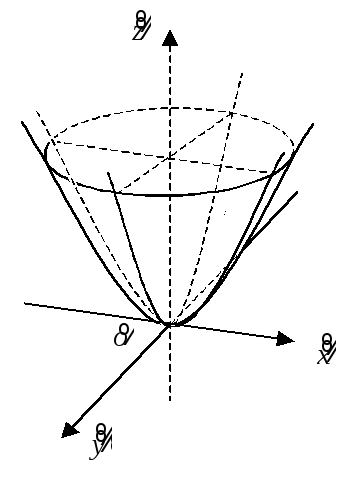
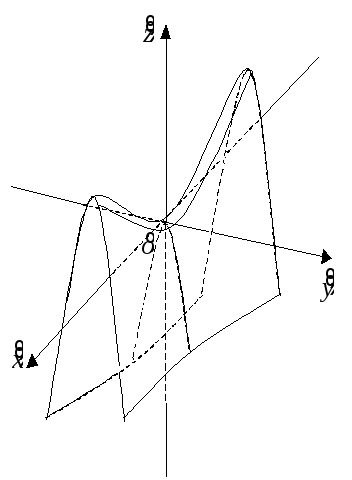
Рис. 8.8 Рис. 8.9

9) эллиптический цилиндр (рис. 8.10);

10) мнимый эллиптический цилиндр ;

11) гиперболический цилиндр (рис. 8.11);

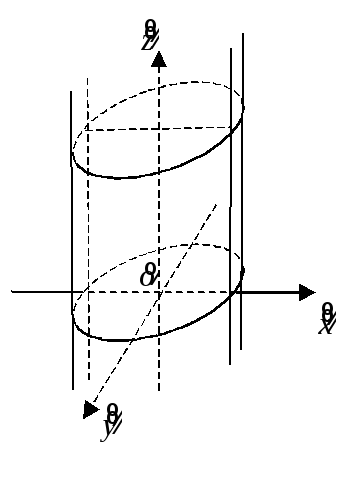
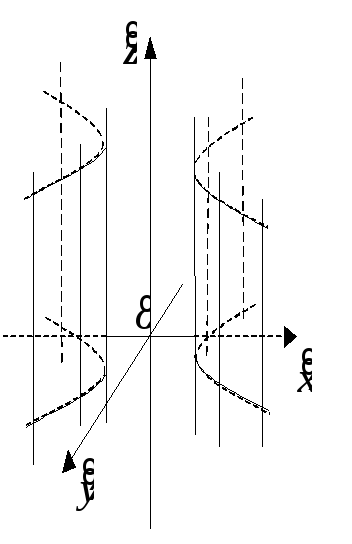
Рис. 8.10 Рис. 8.11

12) параболический цилиндр (рис. 8.12);

13) пара пересекающихся плоскостей ;

14) пара мнимых пересекающихся плоскостей;

15) пара параллельных плоскостей ;

16) пара мнимых параллельных плоскостей ;

17) пара совпадающих плоскостей .

Уравнения 1)–17) называются каноническими уравнениями поверхностей второго порядка.

При преобразовании уравнения поверхности второго порядка (8.5.1) можно, как и в случае кривой второго порядка, использовать инварианты. Инвариантами поверхностей второго порядка являются

,

,

,

.

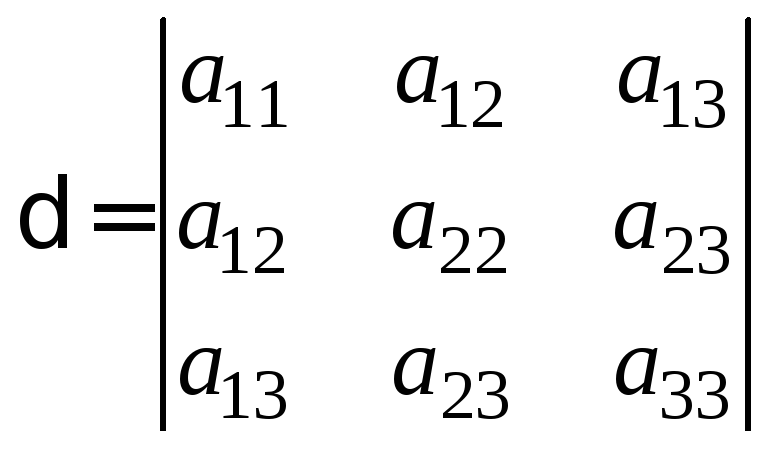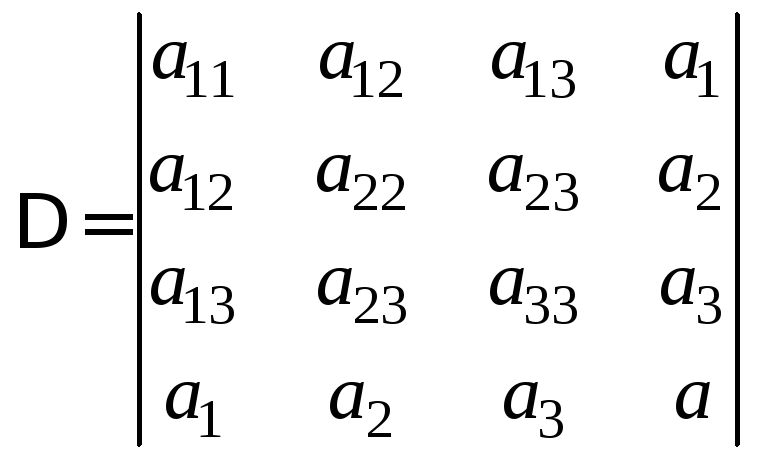Их значения не меняются при повороте и параллельном переносе осей координат.

Пример 1. Поверхность задана уравнением в прямоугольной системе координат

.

Найдите каноническую систему координат и каноническое уравнение этой поверхности. Определите тип поверхности.

Решение. Найдем сначала ортогональное преобразование переменных, приводящее матрицу А квадратичной формы к диагональному виду.

.

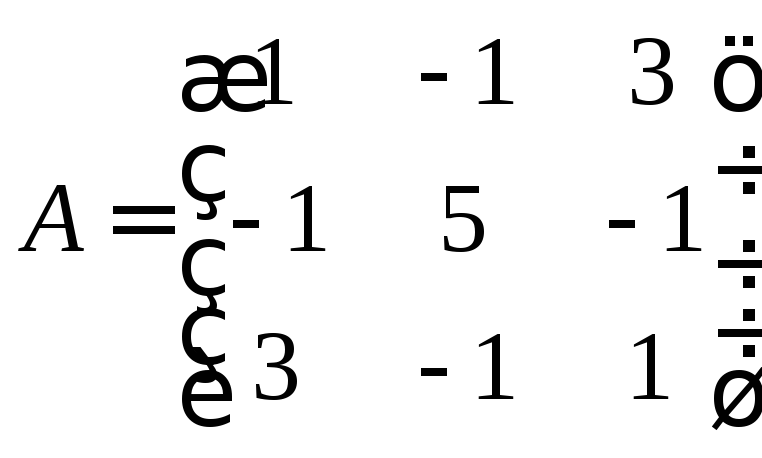Ее характеристический многочлен

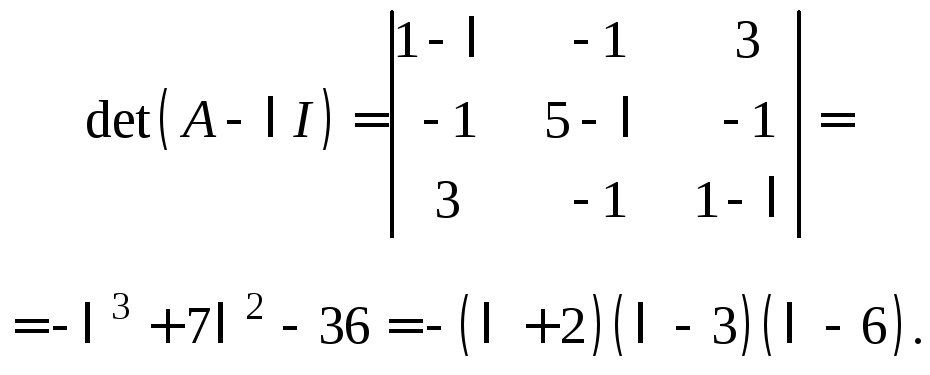
Следовательно, матрица А имеет собственные значения .

Для нахождения собственных векторов матрицы А решаем однородные системы линейных уравнений с матрицами соответственно и выделяем по одному ненулевому решению:

;

;

.

Векторы ортогональны друг другу как собственные векторы симметричной матрицы, соответствующие различным собственным значениям. Нормируя их, получаем

,

,

и матрицу перехода Р к новому ортонормированному базису

.

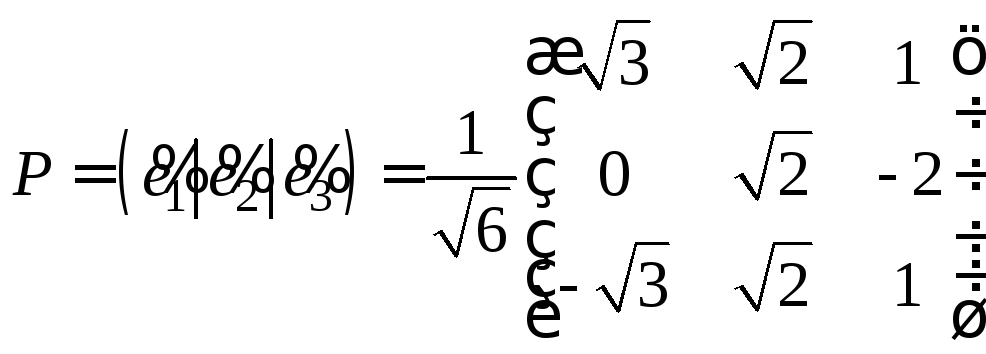Проверим правильность нахождения матрицы Р:

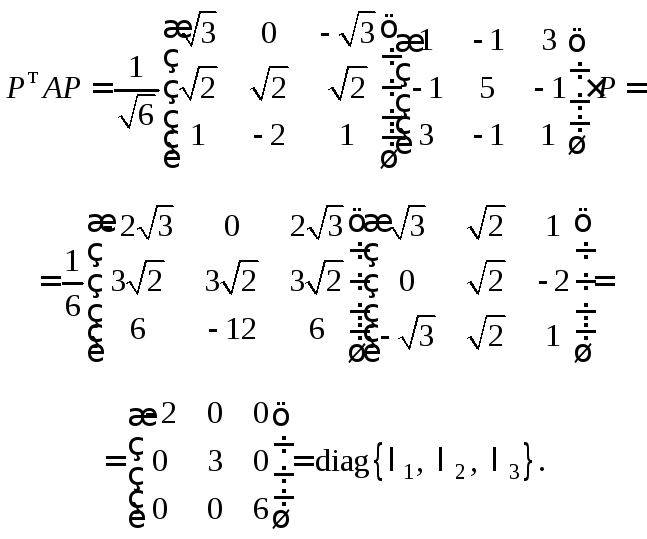
Матрица Р найдена верно.

Применяя к исходному уравнению ортогональное преобразование координат

,

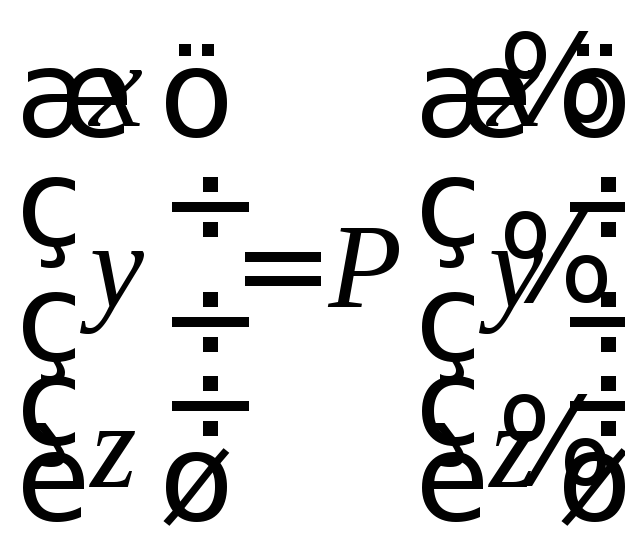получаем новое уравнение поверхности в прямоугольной системе координат со старым центром О и направляющими векторами :

.

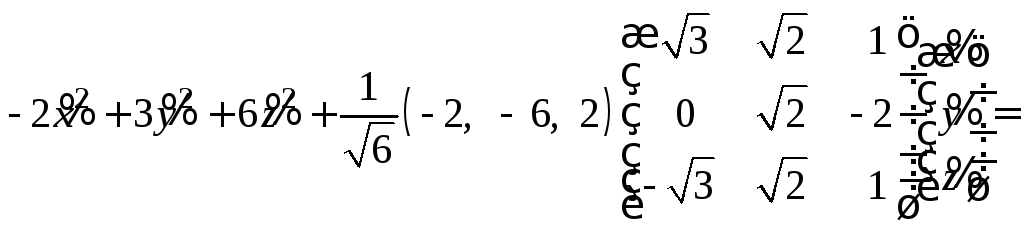
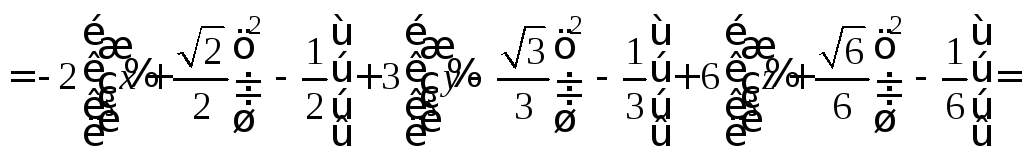
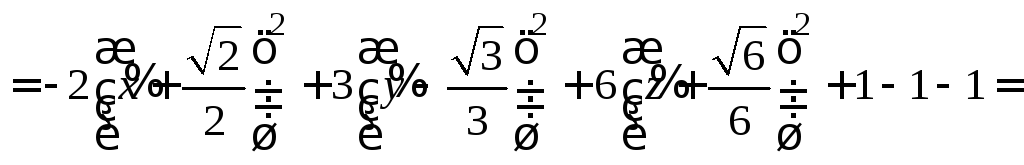
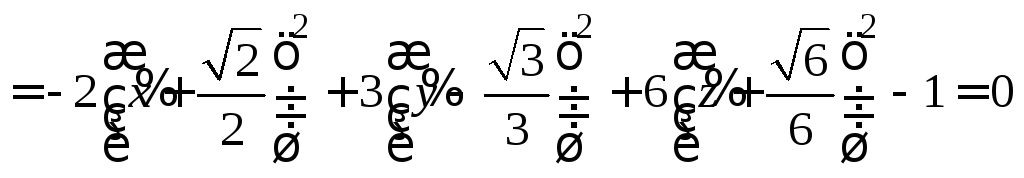Выполняя параллельный перенос системы координат по формулам

приходим к уравнению

,

или

.

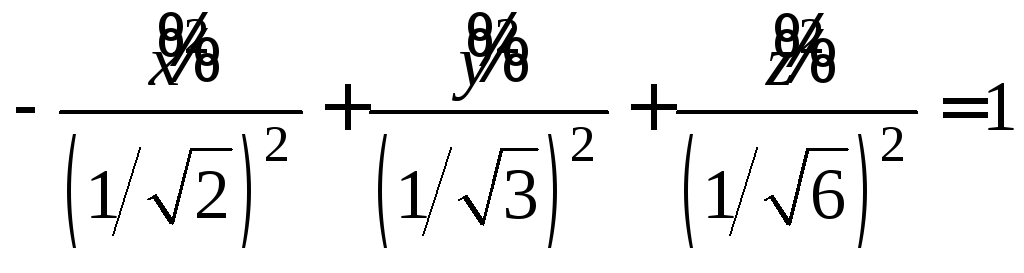Это – каноническое уравнение однополостного гиперболоида в прямоугольной системе координат .

Вычислим координаты начала канонической системы координат в старой прямоугольной системе координат. Поскольку

,

.

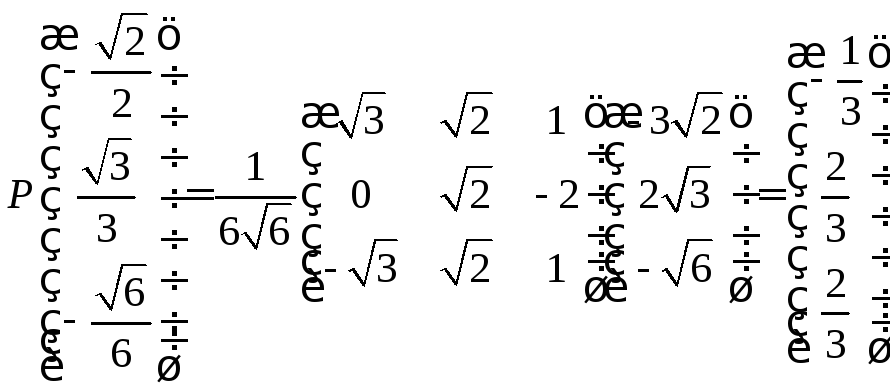Пример 2. Исследуйте поверхность второго порядка, заданную в прямоугольной системе координат уравнением

.

Решение. Начнем с приведения квадратичной формы к каноническому виду. Матрицей этой квадратичной формы является матрица

.

Ее характеристический многочлен

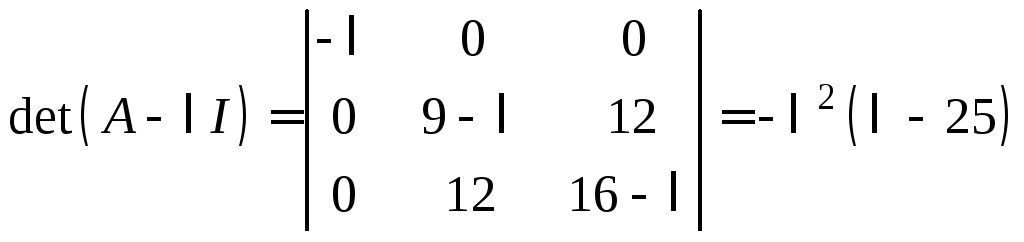
имеет корни . При каждомбудем строить фундаментальную систему решений систем уравненийи ортонормировать их.

При эта система имеет вид

Ее общее решение имеет одну свободную переменную. Поэтому фундаментальная система решений состоит из одного решения, например, из решения. Нормируя его, получим.

При рассматриваемая система имеет вид

Ее общее решение имеет две свободные переменные. Поэтому фундаментальная система решений состоит из двух решений, например, из решенийи. Посколькуивыбраны ортогональными друг к другу (в противном случае требовалось применение процедуры ортогонализации Грама–Шмидта), остается их лишь нормировать. После нормировки получим.

Из столбцов координат векторов составим матрицу переходаР к новому ортонормированному базису

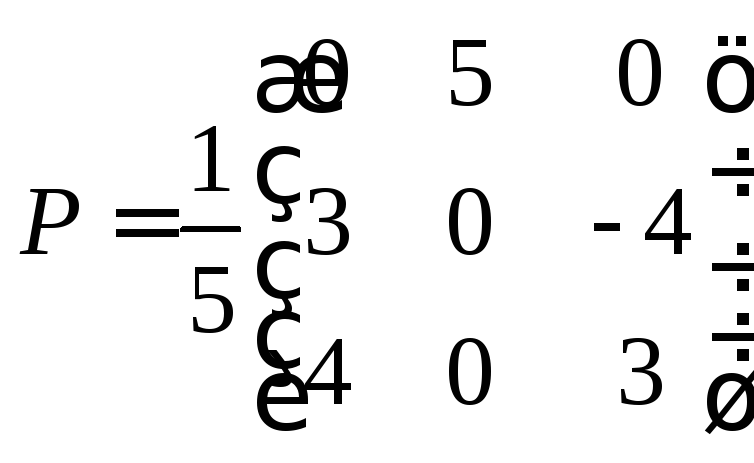
и сделаем проверку

Выполним преобразование координат

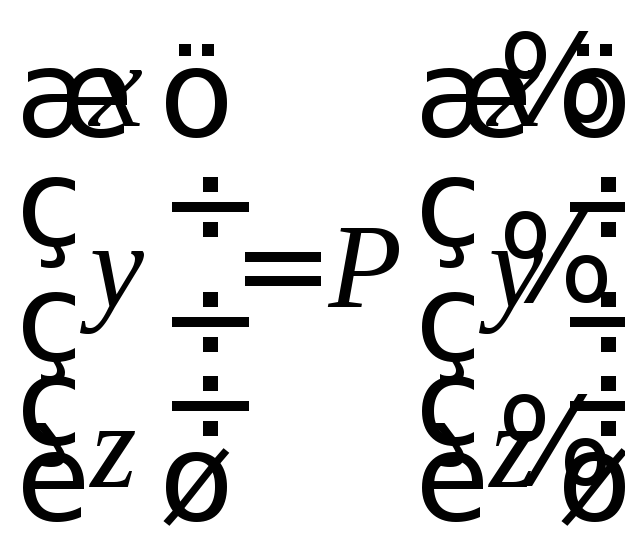
и запишем уравнение данной поверхности в новой прямоугольной системе координат со старым центром О и направляющими векторами :

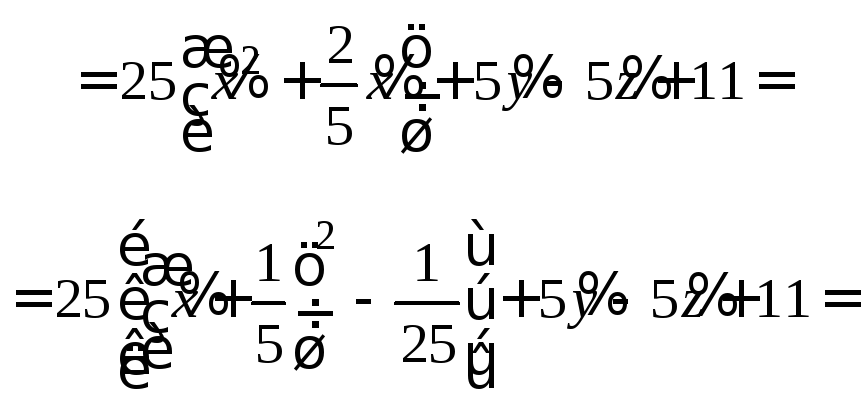
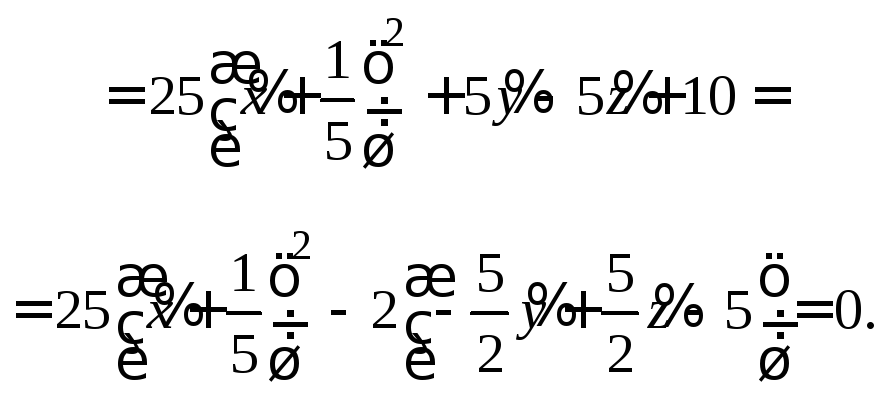
Теперь совершим преобразование координат, полагая

,

,

.

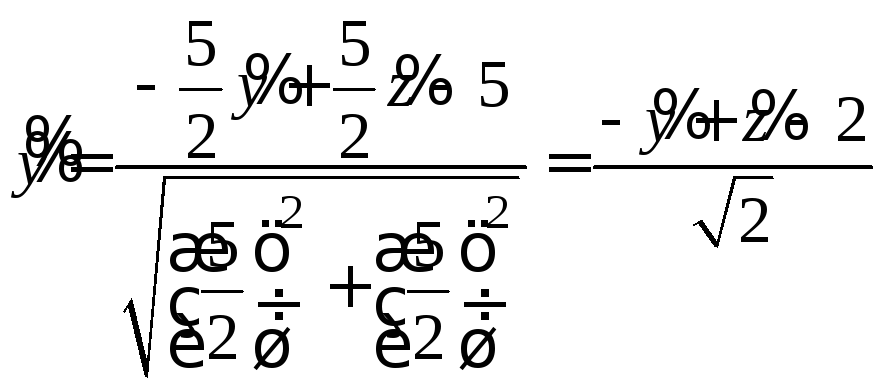При этом коэффициенты выберем так, чтобы матрица формул рассматриваемого преобразования координат была ортогональной, т.е. чтобы векторы-строки

составляли ортонормированную систему векторов. Так как система векторов ортонормированная, то координаты вектораследует искать из условий

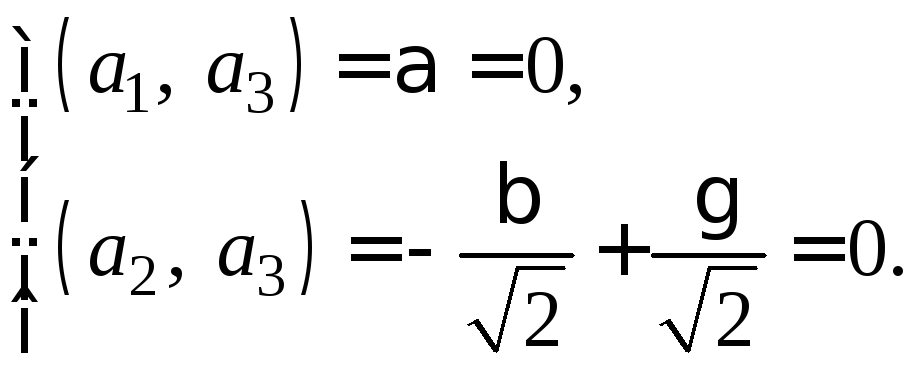
Затем найденный вектор нужно еще нормировать. Проделав это, получим

.

Следовательно, формулы рассматриваемого преобразования координат имеют вид

,

,

,

или

,

,

.

В новых координатах рассматриваемая поверхность имеет уравнение

,

или

.

Это – каноническое уравнение параболического цилиндра в прямоугольной системе координат .

Поскольку

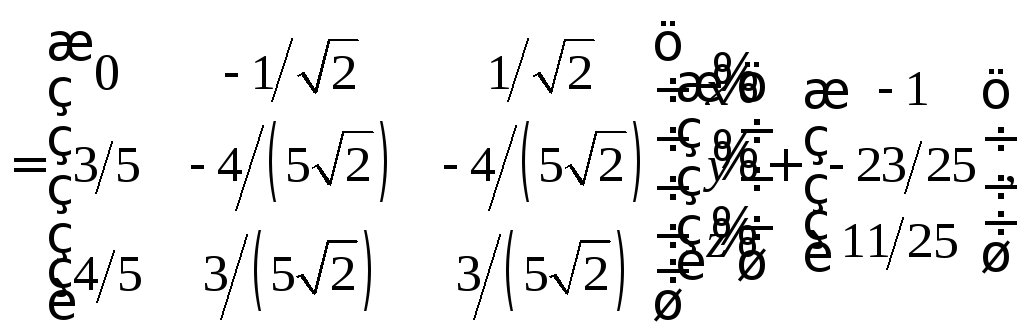
каноническая система координат имеет началои направляющие векторы,,.

В задачах этого параграфа рассматриваются только прямоугольные системы координат.

8.5.1. Семейство поверхностей задано уравнением, содержащим произвольный параметр . Определите тип поверхности при всевозможных :

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) ;

к) ;

л) ;

м) ;

н) ;

о) .

8.5.2. а) Сечения поверхности плоскостями,,спроектированы на плоскостьOyz. Изобразите проекции.

б) Сечения поверхности плоскостями,,спроектированы на плоскостьOyz. Изобразите проекции.

в) Сечения поверхности плоскостями,,спроектированы на плоскостьOyz. Изобразите проекции.

г) Сечения поверхности плоскостями,,спроектированы на плоскостьOxz. Изобразите проекции.

д) Сечения поверхности плоскостями,,спроектированы на плоскостьOxy. Изобразите проекции.

8.5.3. а) Сечения поверхностей ,,плоскостьюспроектированы на плоскостьOyz. Изобразите проекции.

б) Сечения тех же поверхностей плоскостью спроектированы на плоскостьOxy. Изобразите проекции.

8.5.4. По какой линии плоскость пересекает следующую поверхность:

а) ;

б) ;

в) ;

г) ;

д) .

8.5.5. Установите, что плоскость пересекает эллипсоид

по эллипсу, и найдите его вершины и полуоси.

8.5.6. Найдите параметр и вершину параболы, получающейся в пересечении плоскости и гиперболического параболоида

.

8.5.7. Покажите, что плоскость пересекает однополостный гиперболоид

по гиперболе. Найдите полуоси и вершины этой гиперболы.

8.5.8. Приведите уравнения к каноническому виду при помощи перехода к новой прямоугольной системе координат и выясните расположение относительно исходной прямоугольной системы координат следующих поверхностей второго порядка:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) ;

к) ;

л) ;

м) ;

н) ;

о) ;

п) ;

р) .

59