
Ответы и указания
8.1.1.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
8.1.2.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
8.1.3. а) параллельны;
б) пересекаются в точке (–3, 5, –5).
8.1.4. а) a = 3;
б) а 1, а 3;
в) a = –1;
г) a = 1.
8.1.5.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
8.1.6.
![]()
![]() .
.
8.1.7.
а)
![]() ;
;
б)
![]() .
.
8.1.8.
![]() .
.
8.1.9. (3, 11).
8.1.10.
![]() .
.
8.1.11.
![]() .
.
8.1.12. а) 90;
б) 0.
8.1.13.
а)
![]() ;
;
б)
![]()
![]() .
.
8.1.14.
![]() .
.
8.1.15.
![]() .
.
8.1.16.
а)
![]() ;
;
б)
![]() .
.
8.1.17.
а)
![]()
![]()
б)
![]()
![]()
8.1.18.
![]() .
.
8.1.19.
![]() .
.
8.2.1.
![]() .
.
8.2.2.
![]() .
.
8.2.3.
![]() .
.
8.2.4.
![]() .
.
8.2.5.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
8.2.6. А) параллельны;
б) совпадают;
в) пересекаются по прямой.
8.2.7. (5, 0, 0), (0, –5, 0), (0, 0, –5).
8.2.8.
![]() .
.
8.2.9.
![]() .
.
8.2.10. (0, 2, 0).
8.2.11.
![]() .
.
8.2.12.
![]() .
.
8.2.13.
![]() .
.
8.2.14. Указанная плоскость содержит вектор z, но не содержит вектор v.
8.2.15. а) а 3;
б) a = 3;
в) a = –3.
8.2.16.
а)
![]() ;
;
б) 1;
в)
![]() ;
;
г) 1.
8.2.17. а) 2;
б) 5;
в)
![]() .
.
8.2.18.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
8.2.19.
а)
arccos
![]() ;
;
б)
arccos
![]() ;
;
в) 90.
8.3.1. а) прямая лежит в плоскости;
б)
пересечение в точке
![]() ;
;
в) прямая параллельна плоскости.
8.3.2.
а)
![]()
б)
![]() ;
;
в)
![]() .
.
8.3.3.
![]() .
.
8.3.4.
![]() .
.
8.3.5.
![]() .
.
8.3.6.
![]() .
.
8.3.7.
а)
![]() ;
;
б)
![]() .
.
8.3.8. (3, 4, 0).
8.3.9.
![]() .
.
8.3.10.
![]() .
.
8.3.11.
а)
![]() ;
;
б)
![]() .
.
8.3.12.
![]() .
.
8.3.13.
![]() .
.
8.3.14.
![]() .
.
8.3.15. (1, 0, –1) или (–1, –3, –2).
8.3.16.
![]() .
.
8.3.17.
а)
![]() ;
;
б)
![]() ;
;
в) единственная точка (0, 5, 0).
8.3.18. а) 90;
б) 0.
8.3.19.
![]() .
.
8.3.20. (3, 0, 0) или (2, –1, 2).
8.4.1. а) 3 и 5, 5 и 3;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
8.4.2.
![]() .
.
8.4.3.
![]() .
.
8.4.4. а) a = 5, b = 12;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
8.4.5. а) a = 15, b = 8;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
8.4.6.
![]() .
.
8.4.7.
![]() .
.
8.4.8.
![]() .
.
8.4.9.
![]() .
.
8.4.10.
![]() .
.
8.4.11.
а) эллипс
![]()
![]() ;
;
б)
гипербола
![]()
![]() ;
;
в)
парабола
![]()
![]() ;
;
г)
эллипс
![]()
![]() ;
;
д)
парабола
![]()
![]() ;
;
е)
эллипс
![]()
![]() ;
;
ж)
гипербола
![]()
![]() ;
;
з)
парабола
![]()
![]()
![]() ;
;
и)
пара параллельных прямых
![]()
![]() ;
;
![]()
![]() ;
;
к) мнимый эллипс;
л)
пара пересекающихся прямых
![]()
![]() ;
;
![]()
![]()
![]() ;
;
8.4.12.
Длины полуосей равны
![]() и 1, эксцентриситет равен
и 1, эксцентриситет равен
![]() ,
центром является точка
,
центром является точка
![]() ,
уравнение большой оси
,
уравнение большой оси
![]() ,
уравнение малой оси
,
уравнение малой оси
![]() .
Фокусу
.
Фокусу
![]() соответствует директриса
соответствует директриса
![]() ,
фокусу
,
фокусу
![]() соответствует директриса
соответствует директриса
![]() .
.
8.4.13.
Длины обеих полуосей равны
![]() ,
эксцентриситет равен
,
эксцентриситет равен
![]() ,
центром является точка
,
центром является точка
![]() ,
уравнение действительной оси
,
уравнение действительной оси
![]() ,
уравнение мнимой оси
,
уравнение мнимой оси
![]() .
Фокусу
.
Фокусу
![]() соответствует директриса
соответствует директриса
![]() ,
фокусу
,
фокусу
![]() соответствует директриса
соответствует директриса
![]() .
Уравнения асимптот
.
Уравнения асимптот
![]() и
и
![]() .
.
8.4.14.
Параметр параболы равен
![]() ,
вершиной является точка
,
вершиной является точка
![]() ,
фокусом – точка
,
фокусом – точка
![]() .
Осью параболы является прямая
.
Осью параболы является прямая
![]() ,
директрисой – прямая
,
директрисой – прямая
![]() .
.
8.4.15.
а) уравнение
эллипса, которое приводится к виду
![]() преобразованием координат
преобразованием координат
![]() ;
;
б)
уравнение пары пересекающихся прямых,
приводится к виду
![]() преобразованием координат
преобразованием координат
![]() ;
;
в) уравнение
эллипса, которое приводится к виду
![]() путем последовательных преобразований
координат
путем последовательных преобразований
координат
![]() ,
,
![]() и
и
![]() ,
,
![]() ;
;
г) уравнение
параболы, которое приводится к виду
![]() последовательным преобразованием
координат
последовательным преобразованием
координат
![]() ,
,
![]() и
и
![]() ,
,
![]() ;
;
д) уравнение
гиперболы, которое приводится к виду
![]() последовательным преобразованием
координат
последовательным преобразованием
координат
![]() ,
,
![]() и
и
![]() ,
,
![]() ;
;
е) уравнение
параболы, которое приводится к виду
![]() последовательным преобразованием
координат
последовательным преобразованием
координат
![]() ,
,
![]() и
и
![]() ,
,
![]() ;
;
ж) уравнение
пары параллельных прямых, которое
приводится к виду
![]() преобразованием координат
преобразованием координат
![]() ,
,
![]() ;
;
з) уравнение
эллипса, которое приводится к виду
![]() последовательным преобразованием
координат
последовательным преобразованием
координат
![]() ,
,
![]() и
и
![]() ,
,
![]() ;
;
и) уравнение
гиперболы, которое приводится к виду
![]() последовательным преобразованием
координат
последовательным преобразованием
координат
![]() ,
,
![]() и
и
![]() ,
,
![]() ;
;
8.4.16.
а) гипербола
![]() ;
;
б)
эллипс
![]() ;
;
в)
парабола
![]() ;
;
г)
эллипс
![]() ;
;
д)
гипербола
![]() ;
;
е)
парабола
![]() .
.
8.5.1.
а) при
![]() эллипсоид, при
эллипсоид, при
![]() точка, при
точка, при
![]() пустое множество;
пустое множество;
б) при
![]() эллипсоид, при
эллипсоид, при
![]() эллиптический цилиндр, при
эллиптический цилиндр, при
![]() однополостный гиперболоид;
однополостный гиперболоид;
в) при
![]() эллипсоид, при
эллипсоид, при
![]() прямая, при
прямая, при
![]() двуполостный гиперболоид;
двуполостный гиперболоид;
г) при
![]() однополостный гиперболоид, при
однополостный гиперболоид, при
![]() конус, при
конус, при
![]() двуполостный гиперболоид;
двуполостный гиперболоид;
д) при
![]() двуполостный гиперболоид, при
двуполостный гиперболоид, при
![]() конус, при
конус, при
![]() однополостный гиперболоид;
однополостный гиперболоид;
е) при
![]() эллипсоид, при
эллипсоид, при
![]() пара параллельных плоскостей, при
пара параллельных плоскостей, при
![]() двуполостный гиперболоид;
двуполостный гиперболоид;
ж) при
![]() эллипсоид, при
эллипсоид, при
![]() плоскость, при
плоскость, при
![]() однополостный гиперболоид;
однополостный гиперболоид;
з) при
![]() эллиптический параболоид, при
эллиптический параболоид, при
![]() прямая;
прямая;
и) при
![]() эллиптический параболоид, при
эллиптический параболоид, при
![]() параболический цилиндр, при
параболический цилиндр, при
![]() гиперболический параболоид;
гиперболический параболоид;
к) при
![]() эллиптический параболоид, при
эллиптический параболоид, при
![]() плоскость;
плоскость;
л) при
![]() эллиптический параболоид, при
эллиптический параболоид, при
![]() плоскость, при
плоскость, при
![]() гиперболический параболоид;
гиперболический параболоид;
м) при
![]() эллиптический параболоид, при
эллиптический параболоид, при
![]() пара параллельных плоскостей, при
пара параллельных плоскостей, при
![]() гиперболический параболоид;
гиперболический параболоид;
н) при
![]() эллиптический цилиндр, при
эллиптический цилиндр, при
![]() прямая, при
прямая, при
![]() пустое множество;
пустое множество;
о) при
![]() гиперболический цилиндр, при
гиперболический цилиндр, при
![]() пара пересекающихся плоскостей.
пара пересекающихся плоскостей.
8.5.4. а) парабола;
б) эллипс;
в) гипербола;
г) гипербола;
д) гипербола.
8.5.5.
![]()
8.5.6.
![]()
8.5.7.
![]() .
.
8.5.8.
а) мнимый эллиптический цилиндр
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие
векторы канонической
системы координат:
,
направляющие
векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
б)
однополостный гиперболоид
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
в) параболический
цилиндр
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
г) эллипсоид
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
д) эллипсоид
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
е) двуполостный
гиперболоид
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
ж) гиперболический
параболоид
![]() ,
новое
начало координат
,
новое
начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
з) конус
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
и) эллиптический
параболоид
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
к) эллиптический
параболоид
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
л) эллипсоид
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
м) однополостный
гиперболоид
![]() ,
новое начало координат
,
новое начало координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
н)
параболический цилиндр
![]() ,
новое начало координат
,
новое начало координат ![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
о)
однополостный гиперболоид
![]() ,
новое начало
координат
,
новое начало
координат
![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
п) пара пересекающихся плоскостей
![]() ,
,
![]() ;
;
р) параболический
цилиндр
![]() ,
новое начало координат
,
новое начало координат ![]() ,
направляющие векторы канонической
системы координат:
,
направляющие векторы канонической
системы координат:
![]() ,
,
![]() ,
,
![]() ;
;
9.1.1.
а)
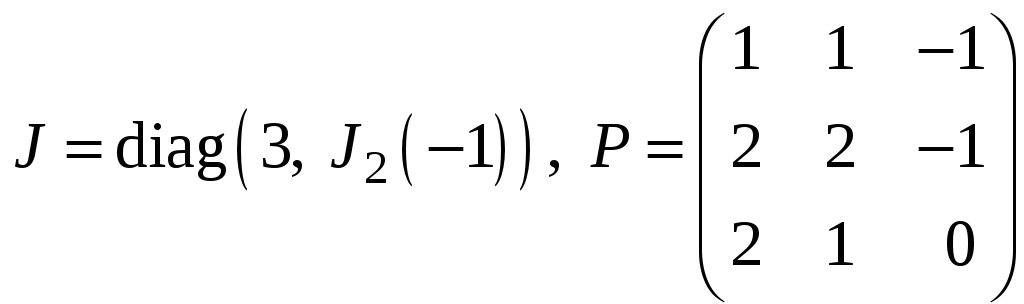 ;
;
б)
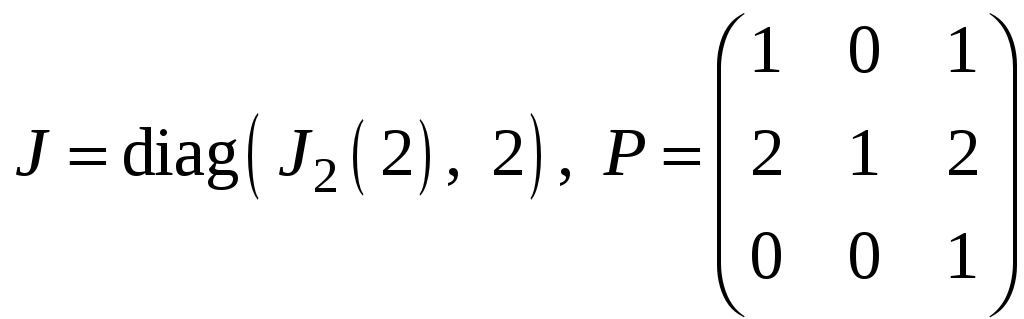 ;
;
в)
 ;
;
г)
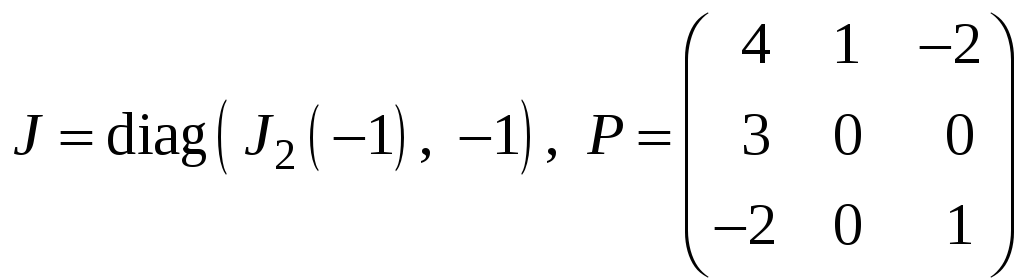 ;
;
д)
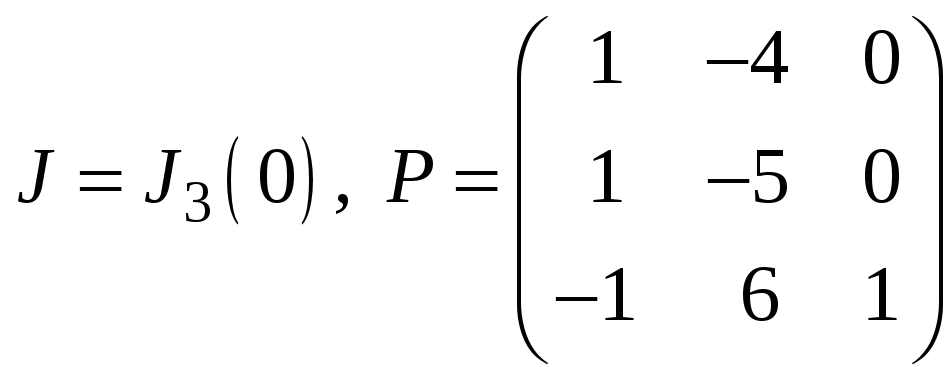 ;
;
е)
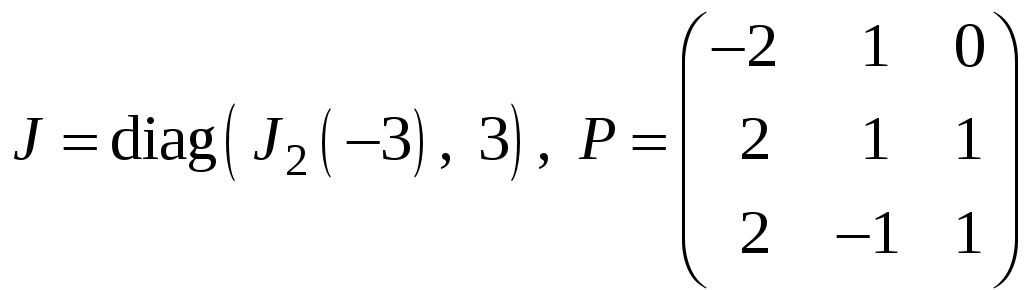 ;
;
ж)
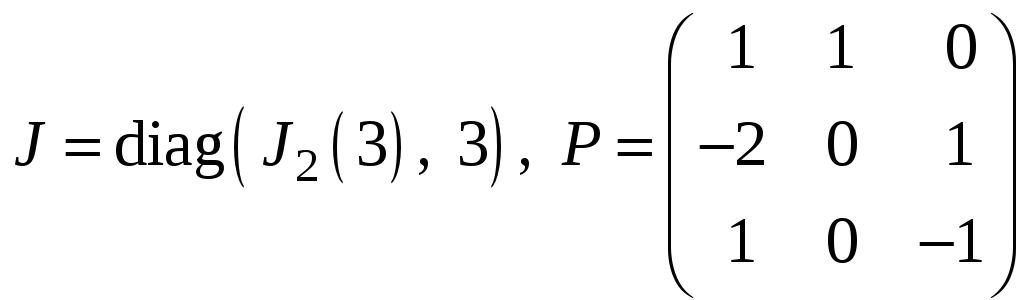 ;
;
з)
 ;
;
и)
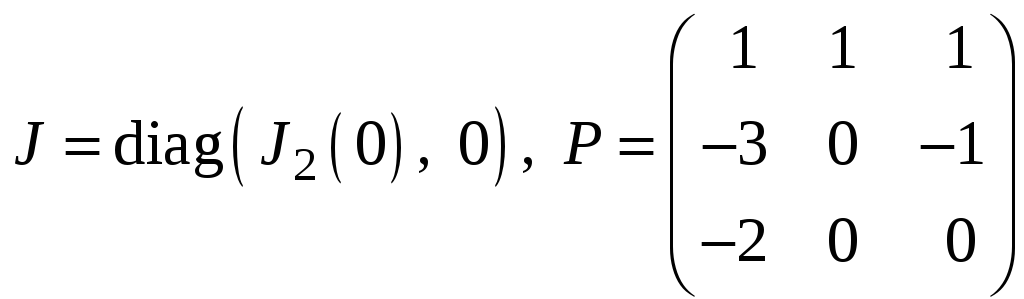 ;
;
к)
 ;
;
л)
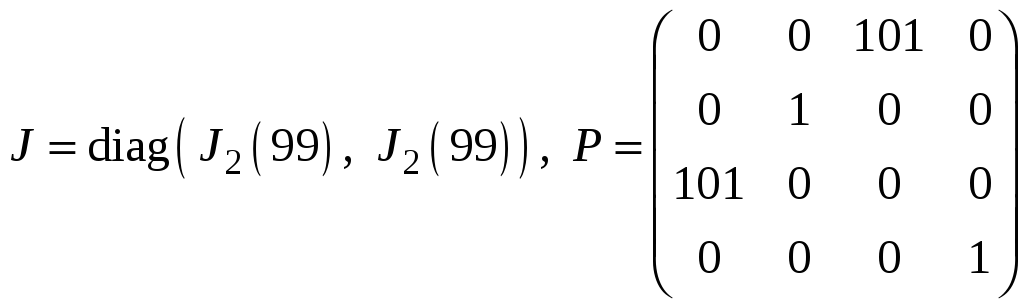 ;
;
м)
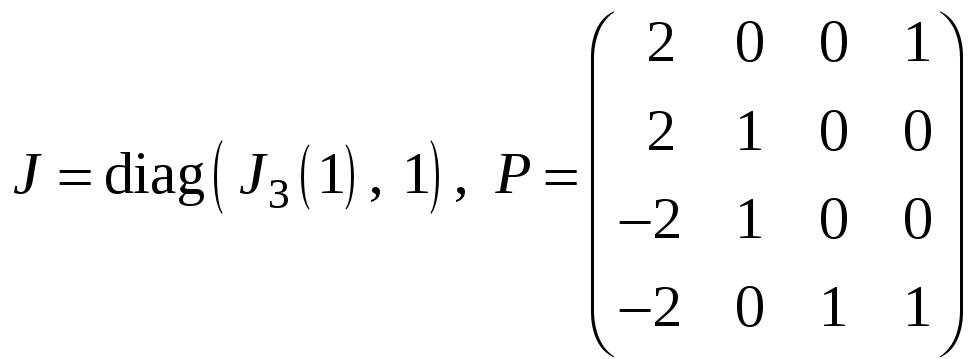 ;
;
н)
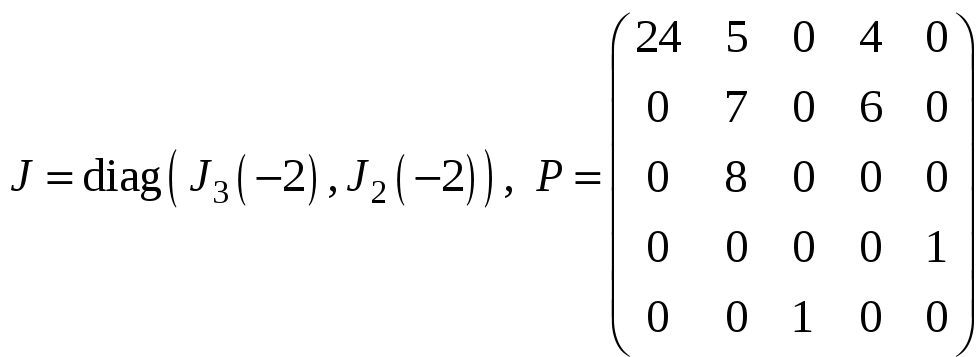 ;
;
о)
 ;
;
п)
 .
.
9.1.2.
 .
.
9.1.3.
![]() .
.
9.1.4.
а)
![]() ;
;
б)
![]() .
.
9.1.5.
а)
![]() ,
где
,
где
![]() ,
,
![]() ,
где
,
где
![]() ,
,
![]() ;
;
б)
![]() .
.
9.1.6. ![]() .
Каноническим является, например, базис
1,
.
Каноническим является, например, базис
1,
![]() ,
,
![]() ,
,
![]() .
.
9.1.7.
![]() .
.
9.2.1.
а)
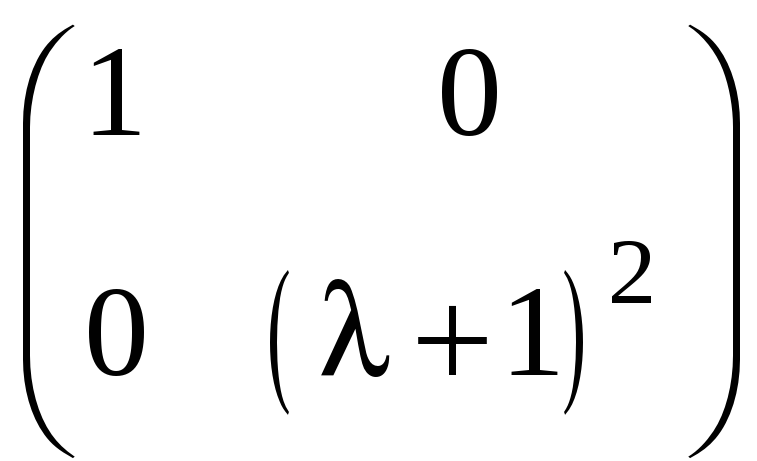 ;
г)
;
г)
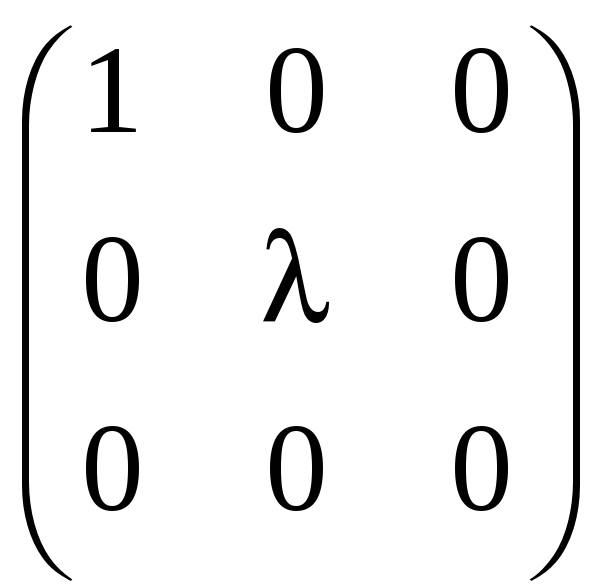 ;
;
б)
![]() ;
д)
;
д)
 ;
;
в)
![]() ; е)
; е)
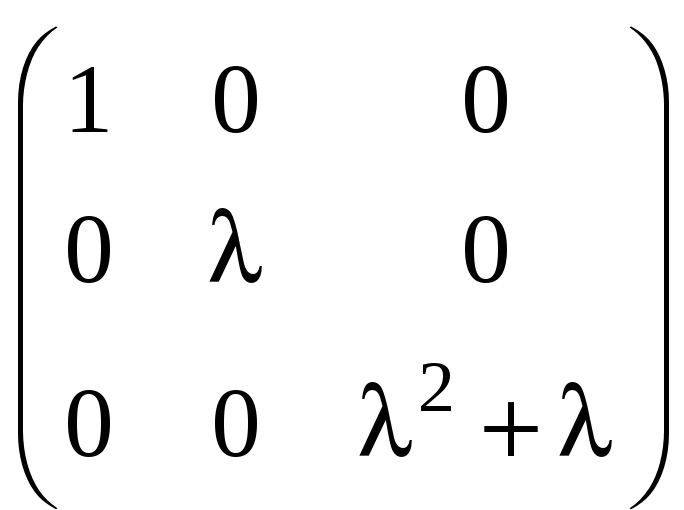 .
.
9.2.2.
а)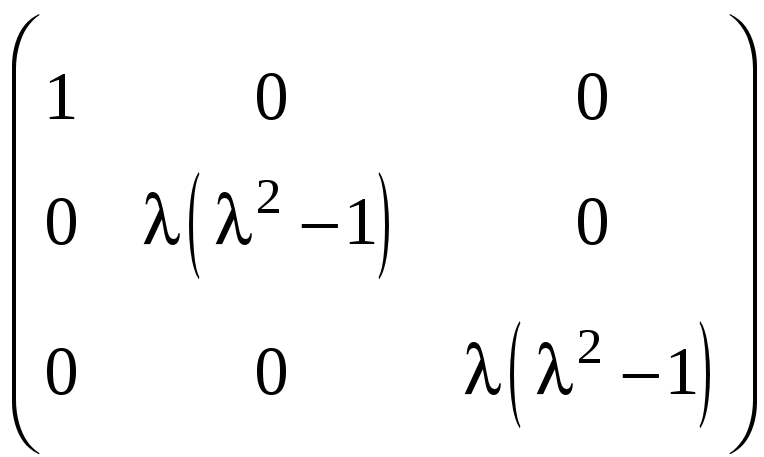 ;
;
б)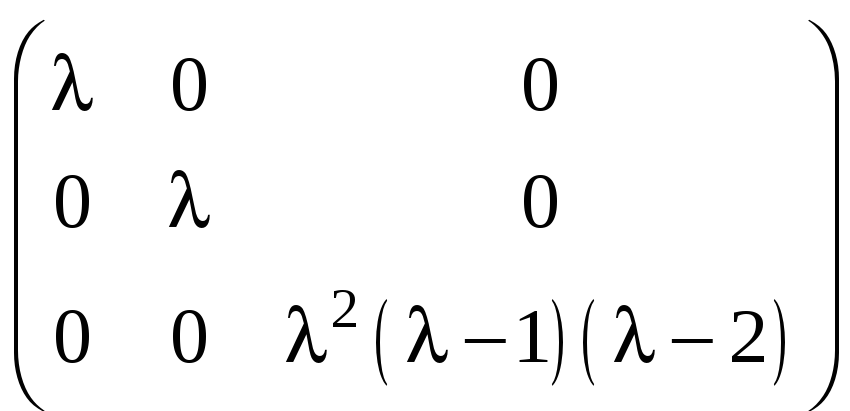 ;
;
в)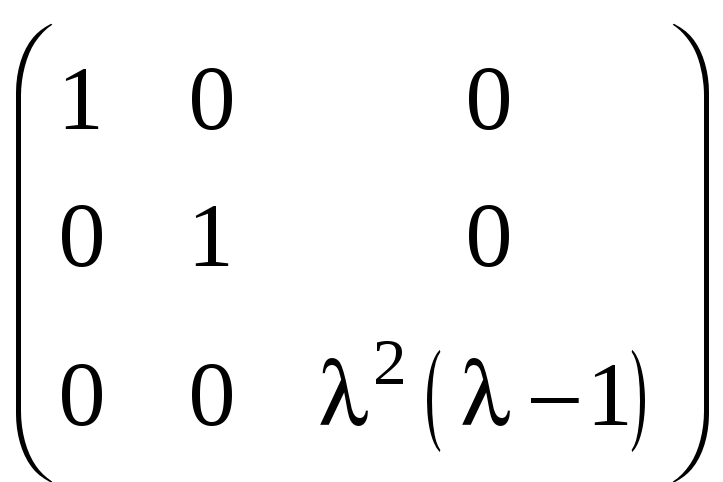 ;
;
г)
 ;
;
д)
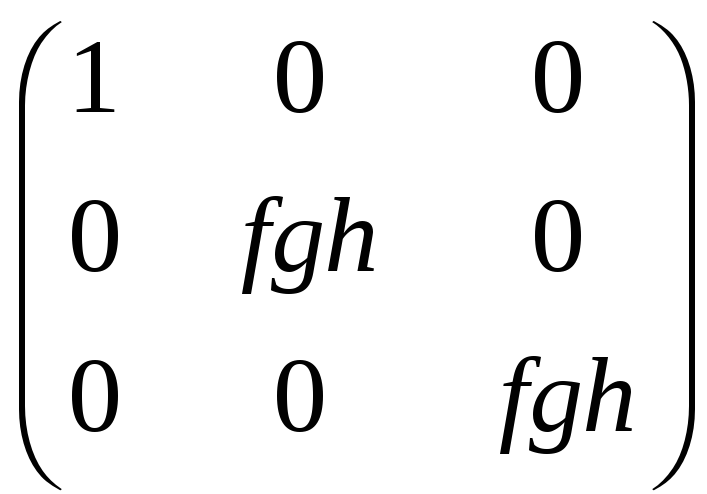 .
.
9.2.3.
а)
![]() ;
;
б)
![]() ;
;
в) задача
поставлена неверно (таких инвариантных
множителей у матрицы
![]() четвертого порядка не может быть).
четвертого порядка не может быть).
9.2.4.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
9.2.5. а) да;
б) да;
в) нет;
г) нет.
9.2.6.
Например,
![]() и
и
![]() .
.
9.2.7.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
10.1.1.
![]()
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
10.1.2.
![]() ,
,
![]() ,
,
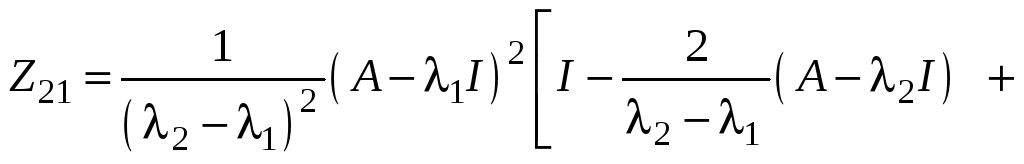
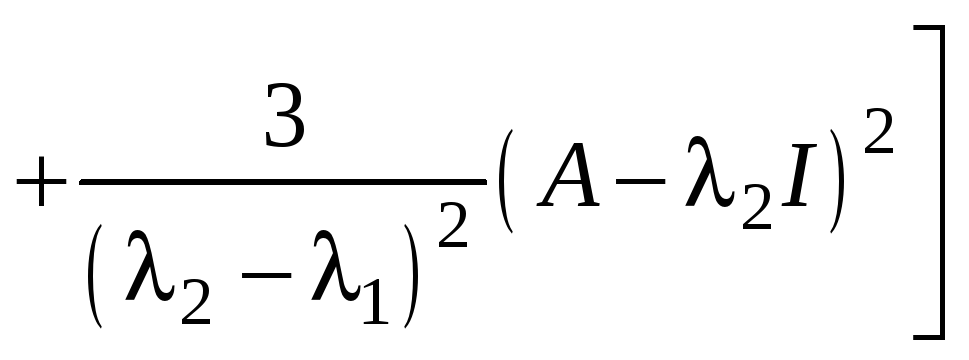 ,
,
![]() ,
,
![]() .
.
10.1.3.
а)
 ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() и
и
![]() ;
;
д)
![]() ;
;
е)
 ;
;
ж)
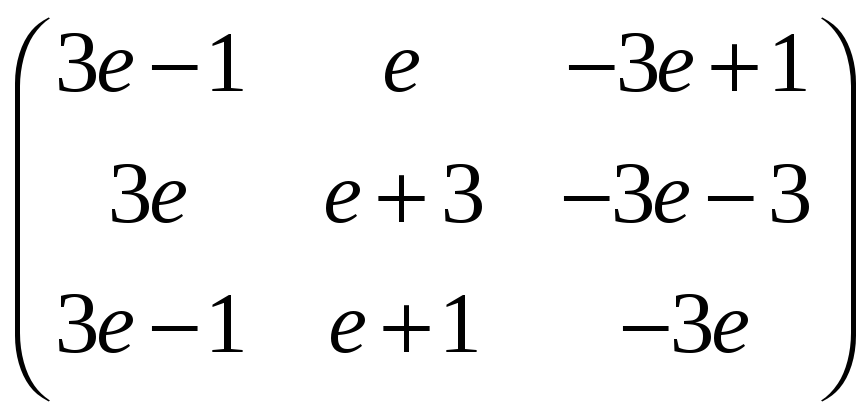 ;
;
з)
 ;
;
и)
![]() ;
;
к)
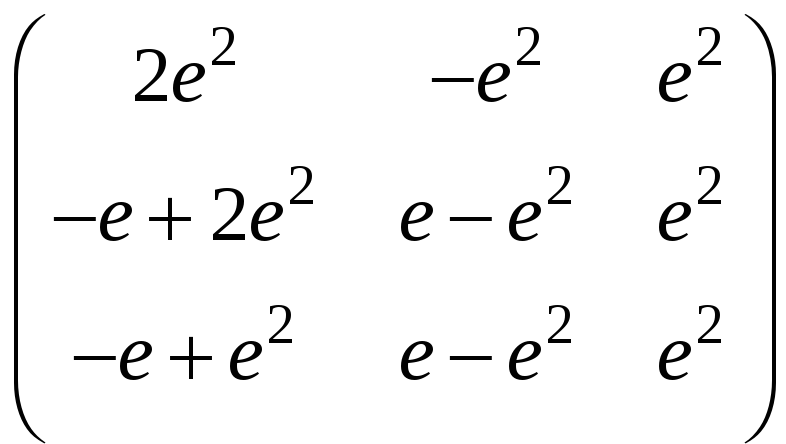 ;
;
л)
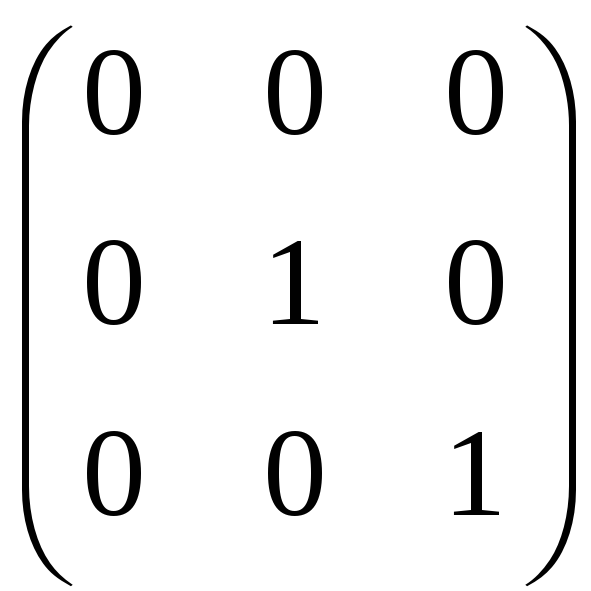 ;
;
м)
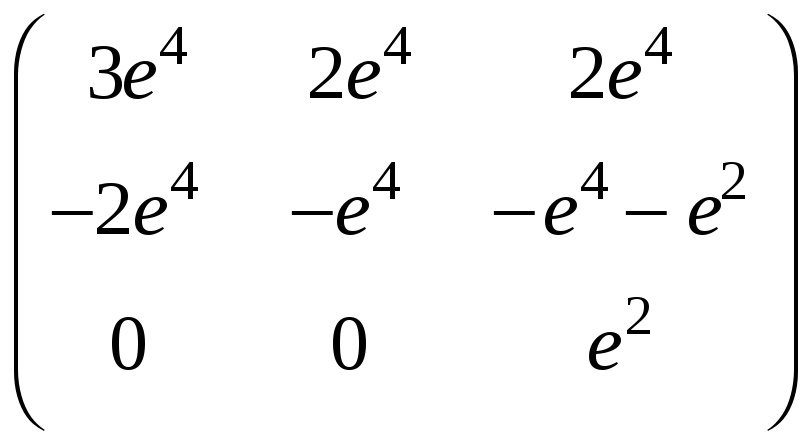 .
.
