
2003_denisov / сборник / Гл. 10
.docГЛАВА 10
ФУНКЦИИ ОТ МАТРИЦ
§ 10.1. ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИЙ ОТ МАТРИЦ РАЗЛИЧНЫМИ СПОСОБАМИ
Пусть
![]() – минимальный многочлен матрицы А
степени
– минимальный многочлен матрицы А
степени
![]() .
Здесь
.
Здесь
![]() – кратность
– кратность
![]() как корня минимального многочлена
как корня минимального многочлена
![]() .
.
Если для функции f(λ) существуют (т.е. имеют смысл) значения
![]()
![]() (10.1.1)
(10.1.1)
то говорят, что функция f(λ) определена на спектре матрицы А, и совокупность m чисел (10.1.1) называют значениями функции f(λ) на спектре матрицы А.
Среди всех многочленов, принимающих те же значения на спектре матрицы А, что и f(λ), существует один и только один многочлен r(λ), имеющий степень, меньшую степени минимального многочлена матрицы А. Этот многочлен однозначно определяется интерполяционными условиями
![]()
![]() (10.1.2)
(10.1.2)
и называется интерполяционным многочленом Лагранжа – Сильвестра для функции f(λ) на спектре матрицы А. Его значение от матрицы А по определению принимается за значение функции f(λ) от этой матрицы: f(A) = r(A).
Заметим,
что если минимальный многочлен
![]() матрицы А
не имеет кратных корней
матрицы А
не имеет кратных корней
![]() ,
то для того, чтобы f(A)
имело смысл, достаточно, чтобы функция
f(λ)
была определена в характеристических
точках
,
то для того, чтобы f(A)
имело смысл, достаточно, чтобы функция
f(λ)
была определена в характеристических
точках
![]() .
Если же
.
Если же
![]() имеет кратные корни, то в некоторых
характеристических точках должны быть
определены и производные от f(λ)
до известного порядка [см. соотношение
(10.1.2)].
имеет кратные корни, то в некоторых
характеристических точках должны быть
определены и производные от f(λ)
до известного порядка [см. соотношение
(10.1.2)].
Если
![]() ,
то минимальным многочленом матрицы А
будет
,
то минимальным многочленом матрицы А
будет
![]() .
Интерполяционный многочлен Лагранжа
– Сильвестра r(λ)
для функции f(λ)
в предположении существования значений
.
Интерполяционный многочлен Лагранжа
– Сильвестра r(λ)
для функции f(λ)
в предположении существования значений
![]() ,
,
![]() ,…,
,…,![]() определится равенством
определится равенством
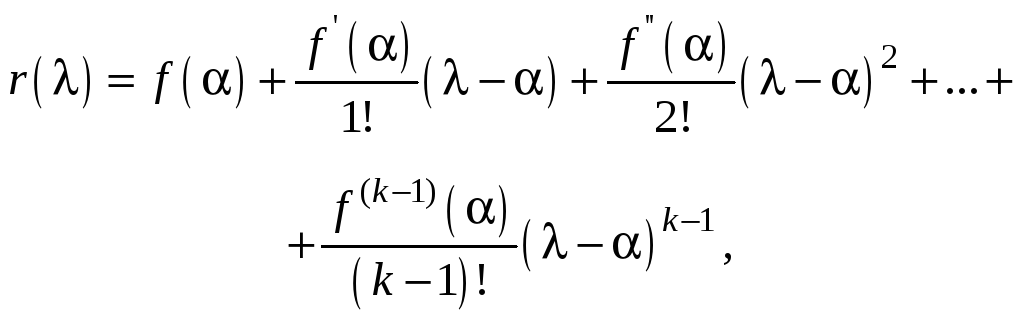
что
позволяет найти значение
![]() :
:
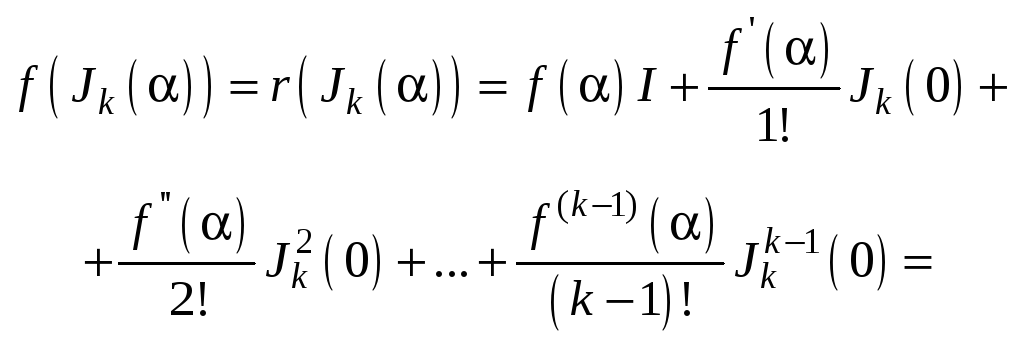
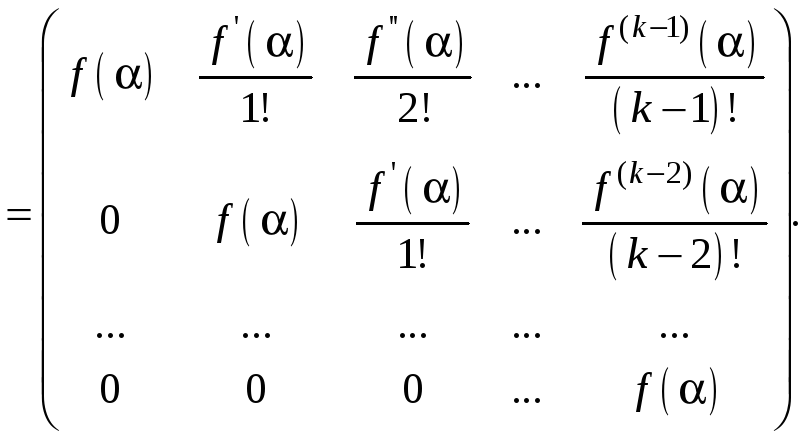 (10.1.3)
(10.1.3)
Подчеркнем два важных для решения задач свойства функций от матриц:
10.
Если две матрицы А
и В
подобны, причем
![]() ,
и для функции f(λ)
матрица f(А)
существует, то и матрица f(В)
существует и подобна f(А),
причем
,
и для функции f(λ)
матрица f(А)
существует, то и матрица f(В)
существует и подобна f(А),
причем
![]() .
.
20.
Если
![]() и функция f(λ)
определена на спектре матрицы А,
то
и функция f(λ)
определена на спектре матрицы А,
то
![]() .
.
Свойства 10, 20 наряду с результатом (10.1.3) используются для вычисления значений функций от матриц через жорданову нормальную форму.
Пусть
функция f(λ)
определена на спектре матрицы А.
Тогда определена матрица f(А)
и, следовательно, существует интерполяционный
многочлен Лагранжа – Сильвестра r(λ).
Если
![]() – минимальный многочлен матрицы А
и корни
– минимальный многочлен матрицы А
и корни
![]() различны между собой, то
различны между собой, то
![]()
![]() (10.1.4)
(10.1.4)
где
![]() ,
(10.1.5)
,
(10.1.5)
а
коэффициенты
![]() определяются из равенств
определяются из равенств
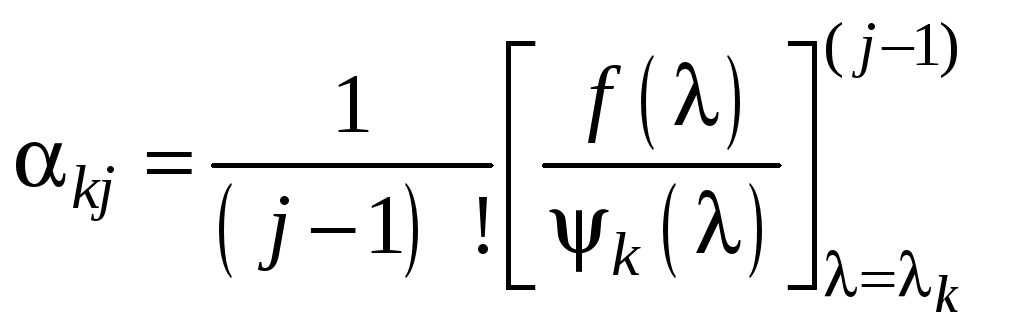
![]() (10.1.6)
(10.1.6)
Заметим,
что выражение в квадратных скобках в
формуле (10.1.4) равно сумме первых
![]() членов разложения в ряд Тейлора по
степеням разности
членов разложения в ряд Тейлора по
степеням разности
![]() для функции
для функции
![]() .
.
Если
в формулу (10.1.4) для r(λ)
подставить выражения (10.1.6) для коэффициентов
![]() ,
раскрыть скобки и объединить члены,
содержащие
,
раскрыть скобки и объединить члены,
содержащие
![]()
![]() ,
то ее можно записать в виде
,
то ее можно записать в виде
![]()
![]() (10.1.7)
(10.1.7)
Из равенства (10.1.7) следует основная формула для f(A):
![]()
![]() (10.1.8)
(10.1.8)
где
![]() .
(10.1.9)
.
(10.1.9)
Матрицы
![]() ,
называемые компонентами
матрицы А,
вполне определяются заданием матрицы
А
и не зависят от выбора функции f(λ).
В правой части формулы (10.1.8) функция
f(λ)
представлена только своими значениями
на спектре матрицы А.
,
называемые компонентами
матрицы А,
вполне определяются заданием матрицы
А
и не зависят от выбора функции f(λ).
В правой части формулы (10.1.8) функция
f(λ)
представлена только своими значениями
на спектре матрицы А.
Формула
(10.1.8) для f(А)
особенно удобна, когда требуется
вычислить несколько функций от одной
и той же матрицы. На практике компоненты
![]() матрицы А
проще находить не по формуле (10.1.9), а из
системы, которая получится в результате
последовательной подстановки в (10.1.8)
вместо f(λ)
простейших линейно независимых
многочленов столько раз, сколько
содержится в (10.1.8) компонент
матрицы А
проще находить не по формуле (10.1.9), а из
системы, которая получится в результате
последовательной подстановки в (10.1.8)
вместо f(λ)
простейших линейно независимых
многочленов столько раз, сколько
содержится в (10.1.8) компонент
![]() .
.
Пример.
Вычислите
![]() при помощи жордановой нормальной формы
матрицы А,
интерполяционного многочлена Лагранжа
– Сильвестра и основной формулы, если
при помощи жордановой нормальной формы
матрицы А,
интерполяционного многочлена Лагранжа
– Сильвестра и основной формулы, если
![]() .
.
Решение. Начнем с построения жордановой нормальной формы J матрицы А и приводящей к ней матрицы Р. Поскольку
![]() ,
,
матрица
А
имеет одно собственное значение
![]() .
Его алгебраическая кратность
.
Его алгебраическая кратность
![]() .
.
![]() .
(10.1.10)
.
(10.1.10)
Геометрическая
кратность
![]() равна
равна
![]() .
Следовательно, жорданов базис будут
составлять собственный вектор
.
Следовательно, жорданов базис будут
составлять собственный вектор
![]() и присоединенный к нему вектор первого
порядка
и присоединенный к нему вектор первого
порядка
![]() ,
удовлетворяющие системам алгебраических
уравнений
,
удовлетворяющие системам алгебраических
уравнений
![]() и
и
![]() .
Общим решением однородной системы с
матрицей (10.1.10) является
.
Общим решением однородной системы с
матрицей (10.1.10) является
![]() .
Поскольку
.
Поскольку
![]() ,
(10.1.11)
,
(10.1.11)
общим
решением неоднородной системы уравнений
(10.1.11) является
![]() .
Выбирая
.
Выбирая
![]() ,
,
![]() ,
получаем жорданов базис, состоящий из
векторов
,
получаем жорданов базис, состоящий из
векторов
![]() ,
,
![]() ,
позволяющий выписать матрицу
,
позволяющий выписать матрицу
![]() ,
приводящую матрицу А
к матрице
,
приводящую матрицу А
к матрице
![]() .
.
Учитывая,
что
![]() и, следовательно,
и, следовательно,
![]() ,
по свойству 10
функций от матриц имеем
,
по свойству 10
функций от матриц имеем
![]() .
Воспользовавшись соотношением (10.1.3)
для
.
Воспользовавшись соотношением (10.1.3)
для
![]() с
с![]() ,
окончательно получаем:
,
окончательно получаем:
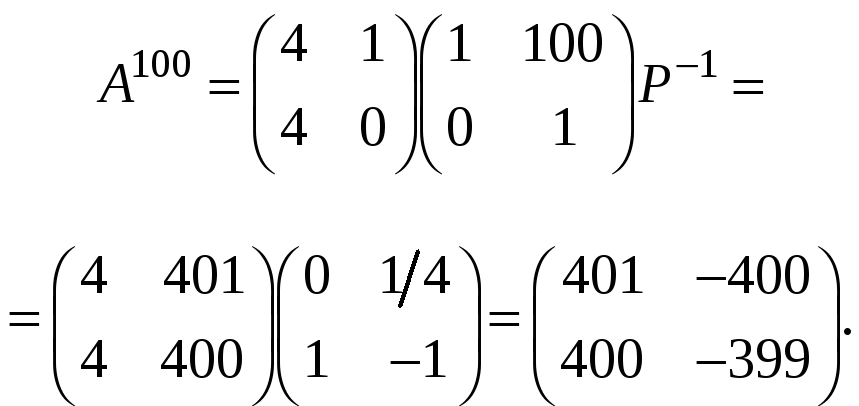
Перейдем
к интерполяционному многочлену Лагранжа
– Сильвестра. Поскольку жорданова
нормальная форма матрицы А
равна
![]() ,
инвариантные множители λ-матрицы
,
инвариантные множители λ-матрицы
![]() таковы:
таковы:
![]() ,
,
![]() .
Поэтому минимальный многочлен матрицы
А
.
Поэтому минимальный многочлен матрицы
А
![]() ,
,
![]()
и соотношение (10.1.4) принимает вид
![]() .
(10.1.12)
.
(10.1.12)
Коэффициенты
![]() и
и
![]() вычислим по формуле (10.1.6):
вычислим по формуле (10.1.6):
![]() ;
;
![]() .
.
Подставляя
найденные значения
![]() и
и
![]() в
равенство (10.1.12), получаем:
в
равенство (10.1.12), получаем:
![]() ,
,
что
позволяет определить
![]() :
:
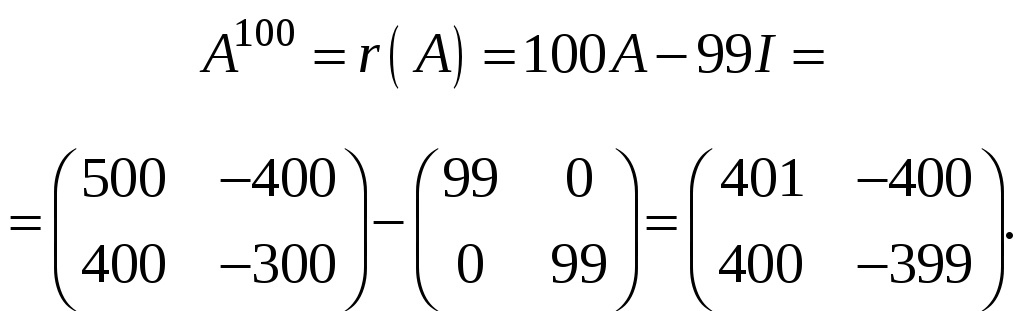
Воспользуемся теперь основной формулой (10.1.8), которая для рассматриваемого случая принимает следующий вид
![]() .
(10.1.13)
.
(10.1.13)
Заменяя
в (10.1.13) f(λ)
на 1, а затем на
![]() ,
находим, что
,
находим, что
![]() и
и
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Полагая
![]() ,
находим
,
находим
![]() .
.
10.1.1
Пусть
![]() – минимальный многочлен матрицы А
и для функции f(λ)
существуют значения
– минимальный многочлен матрицы А
и для функции f(λ)
существуют значения
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Запишите выражение для интерполяционного
многочлена Лагранжа – Сильвестра r(λ)
и вычислите коэффициенты
.
Запишите выражение для интерполяционного
многочлена Лагранжа – Сильвестра r(λ)
и вычислите коэффициенты
![]() ,
определенные соотношением (10.1.4).
,
определенные соотношением (10.1.4).
10.1.2. Найдите компоненты матрицы А с минимальным многочленом ψ(λ), определенным в задаче 10.1.1.
10.1.3. Вычислите следующие значения функций от матриц, пользуясь жордановой нормальной формой, интерполяционным многочленом Лагранжа – Сильвестра и основной формулой:
а)
![]() ,
где
,
где
![]() ;
;
б)
![]() ,
где
,
где
![]() ;
;
в)
![]() ,
где
,
где
![]() ;
;
г)
![]() ,
где
,
где
![]() ;
;
д)
![]() ,
где
,
где
![]() ;
;
е)
![]() ,
где
,
где
![]() ;
;
ж)
![]() ,
где
,
где
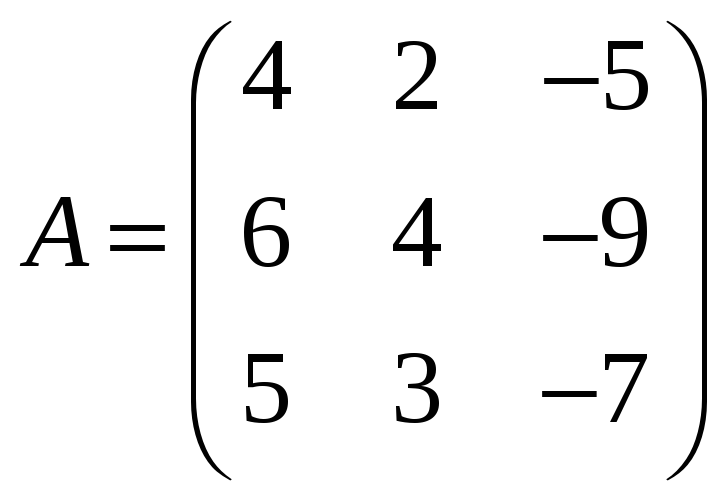 ;
;
з)
![]() ,
где
,
где
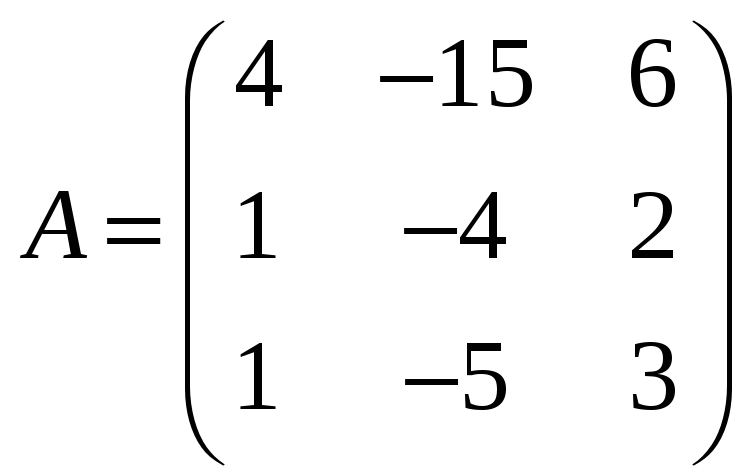 ;
;
и)
![]() ,
где
,
где
![]() ;
;
к)
![]() ,
где
,
где
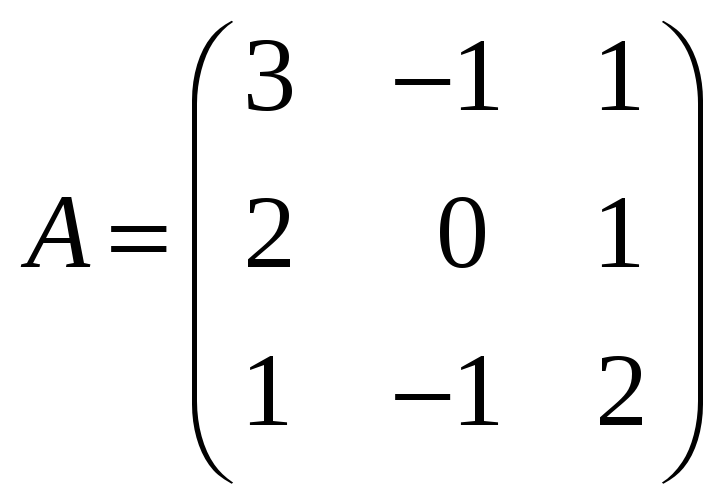 ;
;
л)
![]() ,
где
,
где
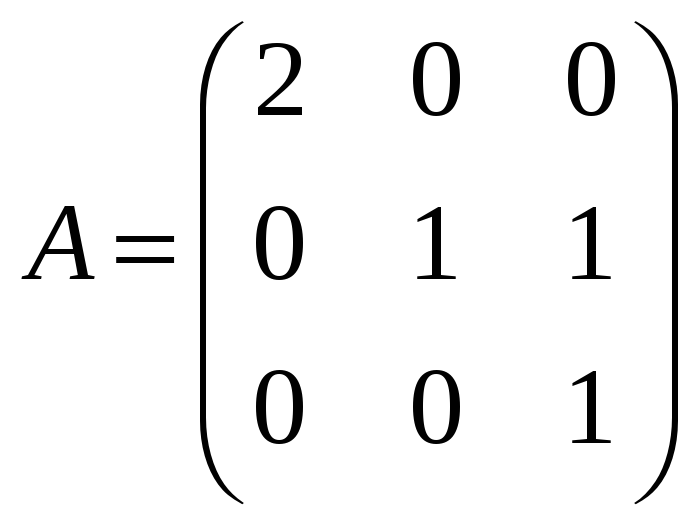 ;
;
м)
![]() ,
где
,
где
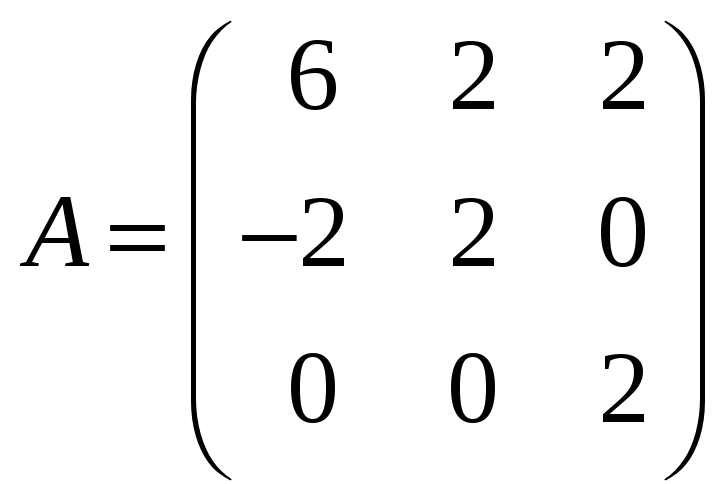 ;
;
