Часть 2. Случайные величины. §1. Одномерные случайные величины.

Пусть () – вероятностное пространство (- пространство элементарных событий,S - -алгебра событий,-вероятности событий);- множество вещественных чисел.

Будем обозначать случайную величину,- принимаемые этой величиной значения.

Случайной величиной называется числовая функция, определённая на пространстве элементарных событий, которая каждому элементарному событиюставит в соответствие число, причем функциядолжна быть такова, чтобы для любого события была определена вероятность .

Случайная величина, принимающая конечное или счётное число значений, называется дискретной.

Закон распределения дискретной случайной величины представляет собой таблицу, в которой значениям, принимаемым случайной величиной, сопоставлены их вероятности, причём, события образуют полную группу событий, то есть(условие нормировки):

			….
P			….

Функцией распределения случайной величины называется функция , которая дляравна вероятности события:

есть неубывающая, непрерывная слева функция, удовлетворяющая свойствам:

1. 

2. 

3. 

Функция распределения дискретной случайной величины.

Плотностью распределения непрерывной случайной величины называется

Свойства.

1. 

2. 

3. 

4. 

Непрерывная случайная величина имеет равномерное распределение на отрезке [a,b], если её плотность распределения:

Причем, константа однозначно определяется условием нормировки:

Основные числовые характеристики.

Математическое ожидание .

Для дискретной случайной величины , принимающей значенияс соответствующими вероятностями:

(ряд предполагается абсолютно сходящимся).

Для непрерывной случайной величины с плотностью распределения :

(интеграл предполагается абсолютно сходящимся).

Начальный момент порядка k:

В случае дискретной случайной величины:

_{В случае непрерывной случайной величины:}

Дисперсия:

Среднее квадратическое отклонение

Центральный момент порядка k:

В частности,

Для дискретной случайной величины:

Для непрерывной случайной величины:

Свойства основных числовых характеристик

MX	DX
X,Y – независимые случайные величины	X,Y – независимые случайные величины

§2. Двумерные случайные величины.

Функцией распределения двумерной случайной величины называется функция

Вероятность попадания в прямоугольник, ограниченный прямыми, параллельными осям координат:

Пусть X – случайная величина с функцией распределения ,Y– случайная величина с функцией распределения ,- функция распределения двумерной случайной величины

Раздел I: Дискретные двумерные случайные величины.

Пусть случайные величины иимеют законы распределения:

			…
P			…

и

Y			…
P			…

Закон распределения двумерной случайной величины (X,Y) имеет вид таблицы:

X\Y	y1	…	ym
x1	P11		P1n
…	…	pij	…
xn	Pn1	…	Pnm

где - значения, принимаемые случайными величинамиX и Y. Вероятности , соответствующие принимаемым значениям, удовлетворяют условию нормировки:

Из распределения двумерной случайной величины

X\Y	y1	y2
x1	P11	P12
x2	P21	P22

можно получить законы распределения для одномерных случайных величин:

X\Y	y1	y2	X
x1	P11	P12	Px1= P11+ P12
x2	P21	P22	px2= P21+ P22
Y	Py1= P11+ P21	Py2= P12+ P22	1

(суммируем вероятности соответственно по строкам и столбцам).

В результате получаем распределение для X:

X	P
x1	Px1= P11+ P12
x2	px2= P21+ P22

И распределение для Y:

Y	y1	y2
P	Py1= P11+ P21	Py2= P12+ P22

Для двумерной дискретной величины функция распределения определяется так:

Разберем пример построения функции распределения в случае, когда случайные величины X и Y заданы распределениями:

P

Y P

Из определения функции распределения двумерной случайной величины в случае дискретной случайной величины следует:

	0	0	0
	0
	0

Получаем функцию распределения :

Для зависимых случайных величин, образующих двумерную систему можно найтиусловные законы распределения и соответствующие им условные математические ожидания.

Условным законом распределения одной из случайных величин, входящих в систему двумерных случайных величин, называется закон ее распределения, найденный при условии, что другая случайная величина приняла определённое значение:

или:

Получаем условный закон распределения для каждого :

			…
			…

Условное математическое ожидание:

Для каждого значения можно вычислить соответствующее математическое ожидание. В результате получаем зависимости.

Функция ) называетсяфункцией регрессии. Графики этих функций называются линиями регрессии.

Замечание. Аналогичным образом можно находить условные математические ожидания при .

Критерии независимости

• Случайные величины инезависимы, если независимы события 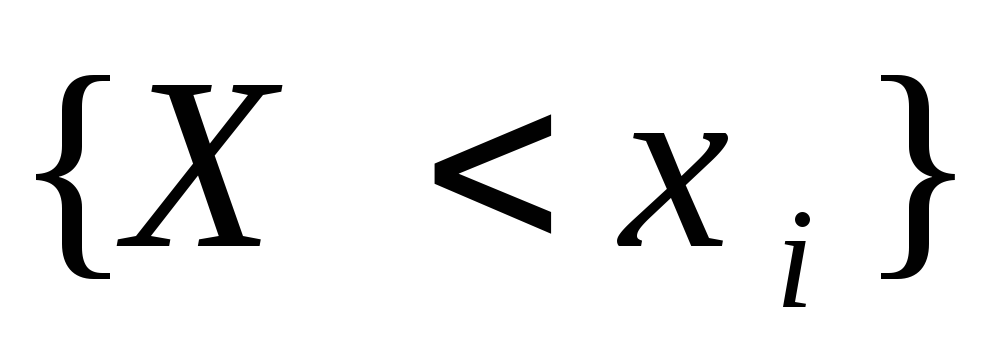и.

• Дискретные случайные величины независимы, если для

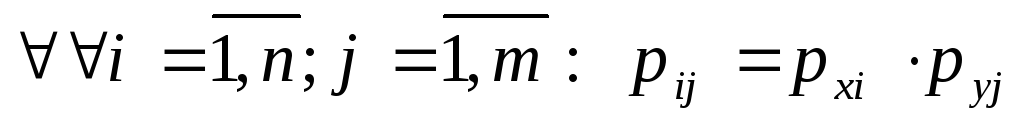
• Случайные величины независимы, если условный и безусловный законы распределения совпадают.

• Случайные величины X и Y независимы, если :

Основные числовые характеристики

Математическим ожиданием двумерной случайной величины называется совокупность математических ожиданий одномерных случайных величин:

Дисперсией двумерной случайной величины называется совокупность двух дисперсий:

Начальным моментом порядкаk+s системы называется

Замечания.

• ,

• Начальный момент 2-го порядка ("смешанное мат. ожидание") вычисляется как:

Центральным моментом порядкаk+s системы называется

Замечание. ,

Математическое ожидание функции случайной величины :

Ковариацией иликорреляционным моментом называется:

Для дискретной случайной величины:

Ковариацию удобнее вычислять по формуле:

Замечания.

а).

б).

в). Для независимых случайных величин

Коэффициентом корреляции называется

,

где ,-средние квадратические отклонения

Замечания.

а).

б). Если случайные величины независимы:

в). Если (случайные величины связаны линейной зависимостью):

(и)

Ковариационной матрицей называется матрица

Задачи к разделу I: Двумерные дискретные случайные величины.

Задания:

1. Записать закон распределения случайного вектора (в виде таблицы)

2. Найти функцию распределения

3. Описать законы распределения отдельных компонент

4. Установить зависимость компонент X и Y

5. Найти условные законы и условные мат. ожидания, построить линии регрессий

6. Найти ковариационную (корреляционную) матрицу

7. Найти

Варианты:

1. Дважды бросается игральная кость. Случайные величины: X – число появлений «5», Y – число появлений четной цифры.

2. Один раз подбрасывается игральная кость. Случайные величины: X – индикатор четного числа выпавших очков, Y – индикатор числа очков, кратного 3.

3. Два игрока – Первый и Второй – наудачу вытаскивают по одному шару из урны, содержащей 6 белых и 4 черных шара. Первый начинает. X – число белых шаров у первого, Y – число белых шаров у второго.

4. Случайная величина X принимает значения 0;1;3 с вероятностями 0,1;0,8;0,1. Случайная величина Y принимает значения -1;0;1 с вероятностями 0,3;0,5;0,2. X и Y независимы.

5. В продукции завода брак с дефектом первого типа составляет 4%, брак с дефектом второго типа – 2%. Годная продукция составляет 96%. X – продукция с браком первого типа, Y – продукция с браком второго типа.

6. Один раз подбрасывается игральная кость. Случайные величины: X – индикатор нечетного числа выпавших очков, Y – индикатор числа очков, кратного 2.

7. Из урны, содержащей 6 белых и 4 черных шара, наудачу извлекают 2 шара без возвращения. Случайные величины: X – число белых шаров в выборке, Y – число черных шаров в выборке.

8. Один раз подбрасывается игральная кость. Случайные величины: X – индикатор четного числа выпавших очков, Y – индикатор числа очков, кратного 2.

9. Бросаются две игральные кости. Случайные величины: X - индикатор четности суммы выпавших очков, Y – индикатор нечетности произведения выпавших очков.

10. В продукции завода брак с дефектом первого типа составляет 2%, брак с дефектом второго типа – 1%. Годная продукция составляет 98%. X – продукция с браком первого типа, Y – продукция с браком второго типа.

11. Два игрока – Первый и Второй – наудачу вытаскивают по одному шару из урны, содержащей 7 белых и 3 черных шара. Первый начинает. X – число черных шаров у первого, Y – число черных шаров у второго.

12. Бросаются две игральные кости. Случайные величины: X - индикатор нечетности суммы выпавших очков, Y – индикатор четности произведения выпавших очков.

13. Два игрока – Первый и Второй – наудачу вытаскивают по одному шару из урны, содержащей 3 белых и 2 черных шара. Первый начинает. X – число белых шаров у первого, Y – число белых шаров у второго.

14. В продукции завода брак с дефектом первого типа составляет 5%, причем среди забракованной по этому признаку продукции в 3% случаев встречается дефект второго типа. В продукции, свободной от дефекта первого типа, дефект второго типа встречается в 2% случаев. X – продукция с браком первого типа, Y – продукция с браком второго типа.

15. Бросаются две игральные кости. Случайные величины: X - индикатор нечетности суммы выпавших очков, Y – индикатор нечетности произведения выпавших очков.

16. Один раз подбрасывается игральная кость. Случайные величины: X – индикатор нечетного числа выпавших очков, Y – индикатор числа очков, кратного 3.

17. Два игрока – Первый и Второй – наудачу вытаскивают по одному шару из урны, содержащей 5 белых и 3 черных шара. Второй начинает. X – число белых шаров у первого, Y – число белых шаров у второго.

18. Дважды бросается игральная кость. Случайные величины: X – число появлений «3», Y – число появлений нечетной цифры.

19. В продукции завода брак с дефектом второго типа составляет3%, причем среди забракованной по этому признаку продукции в 2% случаев встречается дефект первого типа. В продукции, свободной от дефекта второго типа, дефект первого типа встречается в 3% случаев. X – продукция с браком первого типа, Y – продукция с браком второго типа.

20. Два игрока – Первый и Второй – наудачу вытаскивают по одному шару из урны, содержащей 6 белых и 4 черных шара. Первый начинает. X – число белых шаров у первого, Y – число черных шаров у второго.

21. Случайная величина X принимает значения -1;0;1 с вероятностями 0,2;0,5;0,3. Случайная величина Y принимает значения -1;0;1 с вероятностями 0,1;0,1;0,8. X и Y независимы.

22. Дважды бросается игральная кость. Случайные величины: X – число появлений «4», Y – число появлений четной цифры.

23. Один раз подбрасывается игральная кость. Случайные величины: X – индикатор нечетного числа выпавших очков, Y – индикатор числа очков, кратного 5.

24. Два игрока – Первый и Второй – наудачу вытаскивают по одному шару из урны, содержащей 2 белых и 3 черных шара. Первый начинает. X – число белых шаров у первого, Y – число белых шаров у второго.

25. Случайная величина X принимает значения 0;3;6 с вероятностями 0,2;0,7;0,1. Случайная величина Y принимает значения -2;-1;0 с вероятностями 0,2;0,6;0,2. X и Y независимы.

26. В продукции завода брак с дефектом первого типа составляет 3%, брак с дефектом второго типа – 4%. Годная продукция (не содержащая брак с дефектами обоих типов) составляет 95%. X – продукция с браком первого типа, Y – продукция с браком второго типа.