
MMATAN01
.pdf
Задание
1. |
Найти cos arcsin − |
8 |
− arccos |
− |
3 |
!. |
|
|
||
17 |
5 |
|
|
|||||||
2. |
Выразить через арккосинус arcsin |
4 |
− arccos |
5 |
. |
|||||
|
|
|||||||||
5 |
13 |
|||||||||
Доказать справедливость равенств
3.arcctg 2 + arcctg 3 = π4 .
4.arctg x + arcctg x = π2 . Решить уравнения
5.arcsin 2x + arcsin x = π3 .
6.arctg (x − 1) + arctg (x + 1) = π4 .
7.Выразить арккосинус через арктангенс.
Ре ш е н и я
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||
1. |
Введем обозначения arcsin − |
|
|
= α, arccos − |
|
= β. То- |
||||||||||||||||||||||
17 |
5 |
|||||||||||||||||||||||||||
|
гда, используя определения арксинуса и арккосинуса, имеем |
|||||||||||||||||||||||||||
|
|
π |
|
π |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
− |
|
< α < 0, |
|
|
|
< β < π, |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
sin α = −17 , cos α = |
|
|
|
|
|
|
|
= |
17 , |
|
|
|
|
|
|||||||||||||
|
1 − 289 |
|
|
|
|
|
||||||||||||||||||||||
|
|
8 |
|
|
|
|
|
64 |
|
|
|
|
|
15 |
|
|
|
|
|
|
||||||||
|
cos β = −5 , sin β = |
|
|
|
|
= |
|
5 . |
|
|
|
|
|
|
|
|||||||||||||
|
1 − 25 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
3 |
|
|
|
9 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||||
|
Окончательно находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
45 |
|
32 |
|
|
|
77 |
|
||||||||||||
|
cos(α − β) = cos α cos β + sin α sin β = − |
|
|
− |
|
|
= − |
|
. |
|||||||||||||||||||
|
85 |
85 |
85 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
|

|
|
|
4 |
|
|
β = arccos |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2. |
Пусть α = arcsin |
|
, |
|
|
|
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
0 < α < |
π |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
||||||||||||||||||||
|
|
|
|
, 0 < β < |
|
|
|
, |
|
|
|
|
− |
|
|
|
< α − β < |
|
|
|
|
|
, |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
2 |
|
2 |
|
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
sin α = |
4 |
, |
cos α = |
|
3 |
, |
|
|
cos β = |
|
5 |
, |
sin β = |
12 |
. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
5 |
|
|
|
|
|
13 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Уточним интервал, в который попадает угол α−β. Из неравенства |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
sin α = |
|
< |
|
= sin β следует, что α < β и разность α − β |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
13 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
отрицательна, т.е. |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
< α − β < 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Используя неравенство 0 < β − |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
α < |
|
|
|
|
, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
cos(β − α) = cos β cos α + sin β sin α = |
15 |
|
|
48 |
|
|
|
|
63 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
+ |
|
|
|
|
= |
|
, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
65 |
65 |
65 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β − α = arccos |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Окончательно имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
α − β = arcsin |
|
|
− arccos |
|
|
|
|
|
= − arccos |
|
|
|
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
5 |
|
13 |
|
65 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
3. |
Положим α = arcctg 2, |
|
β = arcctg 3, |
0 < α, β < |
π |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Используя формулу для котангенса суммы двух углов, получаем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ctg (α + β) = |
|
ctg α ctg β − 1 |
|
= |
2 · 3 − 1 |
|
= 1. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
ctg α + ctg β |
2 + 3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Откуда с учетом неравенства 0 < α + β < π устанавливаем, что |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α + β = |
π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4. |
При доказательстве используем тот факт, что если тангенсы уг- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
углы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
лов, заключенных в интервале |
|
|
|
|
|
|
π |
|
, |
π |
|
|
|
, равны, то равны и эти |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
tgπ |
|
|
|
|
tg |
β, |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
α = β. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
α = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
< α, β < |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
82 |
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
π |
||||||
Рассмотрим углы arctg x и |
|
|
− arcctg x. Оба угла заключены в |
||||||||||||||
2 |
|||||||||||||||||
интервале − |
π |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
, |
|
, так как по определению арктангенса |
||||||||||||||
2 |
2 |
||||||||||||||||
|
|
|
|
|
− |
π |
|
< arctg x < |
π |
||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
2 |
2 |
|||||||||||
По определению арккотангенса 0 < arcctg x < π и поэтому |
|||||||||||||||||
|
|
|
|
− |
π |
|
π |
|
− arcctg x < |
π |
|||||||
|
|
|
|
|
< |
|
|
|
|
|
. |
||||||
|
|
|
|
2 |
|
|
2 |
|
2 |
||||||||
Тангенсы этих углов совпадают: |
|||||||||||||||||
tg ( arctg x) = x, |
tg |
π |
|
− arcctg x = ctg ( arcctg x) = x. |
|||||||||||||
|
|
||||||||||||||||
2 |
|
||||||||||||||||
Следовательно, эти углы равны
arctg x = π2 − arcctg x.
5.Очевидно, что неизвестное x должно быть положительным, так как при x ≤ 0 в силу свойств арксинуса arcsin 2x + arcsin x ≤ 0.
Введем обозначение |
α = |
arcsin 2x, |
|
β = |
arcsin x. Тогда 0 < |
|||||||||||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
α, β ≤ |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin α = 2x, cos α = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 − 4x2, sin β = x, |
|
cos β = 1 − x2. |
|||||||||||||||||
Используя соотношение cos(α + β) = |
1 |
, запишем уравнение для |
||||||||||||||||||
|
||||||||||||||||||||
2 |
||||||||||||||||||||
нахождения x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 − 4x2 |
|
|
|
1 − x2 − 2x2 = |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решая его находим x = |
|
. |
|
|
|
|
|
|
||||||||||||
28 |
|
|
|
|
|
|
||||||||||||||
6.Аналогично предыдущей задаче можно установить ограничение x + 1 > 0.
83

Обозначая α = arctg (x − 1), β = arctg (x + 1), получаем уравнение для нахождения x
tg α = x − 1, tg β = x + 1, |
|
|
||||
tg (α + β) = 1, |
|
tg α + tg β |
= 1, |
2x |
|
= 1, |
|
− tg α tg β |
1 − (x2 |
|
|||
1 |
|
− 1) |
||||
x2 + 2x − 2 = 0.
Решая это уравнение с учетом ограничения на x, получаем
√
x = 3 − 1.
7.Пусть 0 < x ≤ 1. В этом случае 0 ≤ arccos x < π2 и область изменения арккосинуса совпадает с областью изменения арктангенса. Обозначим α = arccos x. Тогда
√√
cos α = x, tg α = |
1 − cos2 α |
= |
1 − x2 |
|
cos α |
x |
|||
|
|
√
и α = arctg 1 − x2 при 0 < x ≤ 1. x
При −1 ≤ x < 0 имеем:
|
|
arccos x = π − arccos(−x) = |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
= π |
|
|
|
2 |
|
= π + |
|
|
|
|
|
2 |
|
|
||||||||
− arctg |
|
1 − x |
arctg |
|
1 − x . |
|
||||||||||||||||
Итак, |
|
|
−x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
0 < x |
|
|
|
1, |
|||||||
|
|
|
arctg |
1 − x2 |
, |
если |
≤ |
|||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||
arccos x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
− |
x |
, |
|
|
|
1 |
|
|
x < 0. |
|||||||
|
|
π + |
arctg |
|
|
|
|
|
|
если |
− |
≤ |
||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
84

Задачи для самостоятельного решения
Вычислить
|
1 |
|
+ arctg |
1 |
|
|
1. tg |
arcsin |
√ |
|
|
. |
|
|
9 |
|||||
|
5 |
2 |
|
|
|
|
Доказать равенства
3. arcsin x + arccos x = π2 .
5. arctg (−x) = − arctg x.
7. arcctg (−x) = π − arcctg x.
|
|
33 |
|
2. arcsin |
cos |
5 |
π . |
4. arcsin(−x) = − arcsin x.
6. arccos(−x) = π − arccos x.
8.Решить уравнение arcsin 3x + arcsin 4x = π2 .
9.Выразить арккосинус через арксинус.
Ответы
1. 31 . 2. − |
10 . 8. |
5 . 9. |
|
|
|
|
, |
−1 ≤ x ≤ 0. |
||
π − arcsin−√1 − x2 |
||||||||||
8 |
|
π |
1 |
|
arccos x = arcsin √1 |
x2, |
|
0 ≤ x ≤ 1, |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
Занятие 3. Преобразование графиков
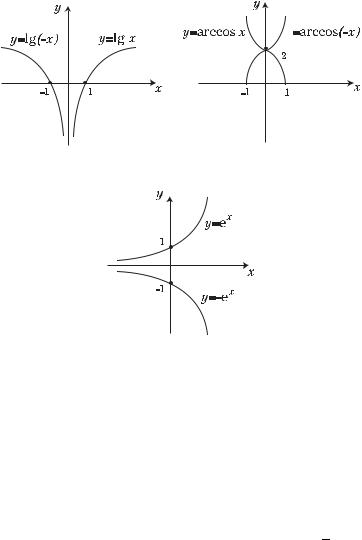
1. Смена знака у аргумента. График функции y = f (−x) получается симметричным отображением графика функции y = f (x) относительно оси y.
П р и м е р 1. На рис. 2.11 пунктиром изображены графики функций y = lg x и y = arccos x, сплошной линией — графики функций
y= lg(−x) и y = arccos(−x).
2.Смена знака у функции. График функции y = −f (x) (−y = f (x)) получается симметричным отображением графика функции
y= f (x) относительно оси x.
85
 π
π
π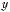
Рис. 2.11
Рис. 2.12
П р и м е р 2. На рис. 2.12 пунктиром изображен график функции y = ex, сплошной линией — график функции y = − ex.
3. Изменение аргумента на постоянное число. График функции y = f (x − a) получается из графика функции y = f (x) смещением (параллельным переносом) на a единиц вдоль положительного направления оси x (вправо), если a > 0, и на |a| единиц вдоль отрицательного направления оси x (влево), если a < 0.
П р и м е р 3. Построить графики функций y = 12 2x и y =
arcsin( x + 1). Первая функция преобразуется к виду y = 2x−1, и ее график получается из графика функции y = 2x смещением на
86
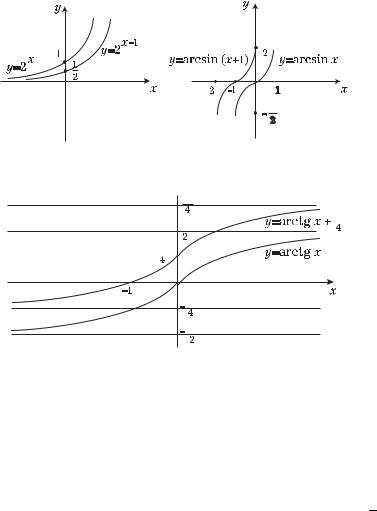
единицу вправо, второй график получается из графика функции y = arcsin x смещением на единицу влево (рис. 2.13).
π
π
Рис. 2.13
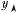
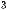 π
π
π |
π |
|
π
π
π
Рис. 2.14
4. Изменение значения функции на постоянное число. График функции y − b = f (x) (или y = f (x) + b) получается из графика функции y = f (x) смещением на b единиц вдоль положительного направления оси y (вверх), если b > 0, и на |b| единиц вдоль отрицательного направления оси y (вниз), если b < 0.
П р и м е р 4. На рис. 2.14 пунктиром изображен график функции y = arctg x, сплошной линией — график функции y = arctg x + π4 .
87
5. Параллельный перенос вдоль обеих координатных осей. График функции F (x − a, y − b) = 0 получается из графика F (x, y) = 0 последовательным применением предыдущих преобразований 3 и 4.
П р и м е р 5. График (x − 1)2 + (y + 1)2 = 1 можно получить из графика x2 + y2 = 1 перемещением влево и вниз на единицу (рис. 2.15).
Рис. 2.15
6. График четной функции. График четной функции симметричен относительно оси ординат. Его строят сначала при x ≥ 0 и затем отражают относительно оси y.
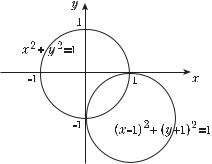
П р и м е р 6. На рис. 2.16 изображены графики четных функций
y= lg x2 и y = x2 − 3|x| + 2.
Вчастности, функция y = f (|x|) — четная и ее график состоит из двух частей: y = f (x) при x ≥ 0 и симметрично отраженной относительно оси ординат части y = f (−x) при x < 0. Иными словами, та часть графика y = f (x), которая лежит правее оси ординат, остается без изменения, а затем добавляется эта же часть, симметрично отраженная относительно оси ординат. Это преобразование мы будем называть симметричным продолжением правой части графика функции y = f (x) (относительно оси ординат).
88
y |
y |
|
2
-1 |
1 |
x |
-2 |
-1 |
1 |
|
2 |
x |
y=lgx 2 |
|
|
|
|
y=x |
2 |
-3|x|+2 |
|
|
|
|
|
|
|
|
Рис. 2.16
7. График нечетной функции. График нечетной функции симметричен относительно начала координат. Его строят сначала при x ≥ 0, а затем симметрично отражают относительно начала координат.
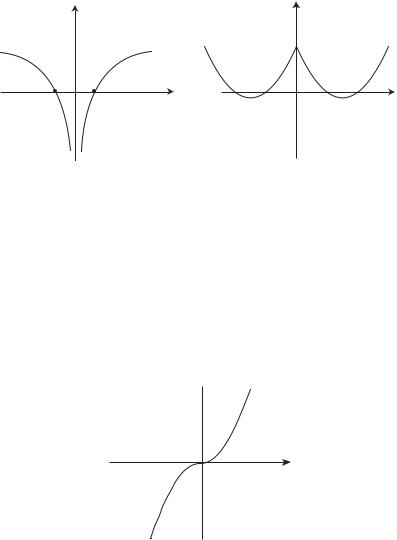
П р и м е р 7. График функции y = x|x| изображен на рис. 2.17. При x ≥ 0 он совпадает с параболой y = x2.
y 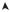
x
y=x|x|
Рис. 2.17
89
8. График функции y = |f (x)|. Используя определение модуля действительного числа, можем записать
| |
| |
|
f (x), |
если f (x) < 0. |
y = |
f (x) = |
f (x), |
если f (x) ≥ 0, |
|
|
|
− |
|
|
Откуда следует правило построения этого графика: та часть графика функции y = f (x), которая лежит выше оси x, остается без изменения, а часть графика, лежащая ниже оси x, симметрично (относительно оси абсцисс) отображается вверх.
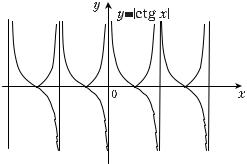
П р и м е р 8. На рис. 2.18 сплошной линией изображен график функции y = | ctg x|.
−2π |
−π |
π |
2π |
Рис. 2.18
9. График функции |y| = |f (x)|. В силу свойств модуля
|y| = |f (x)| y = ±f (x).
Откуда следует, что для того чтобы построить график |y| = |f (x)|, нужно к графику y = f (x) добавить график y = −f (x) (симметрично продолжить график y = f (x) относительно оси абсцисс).
П р и м е р 9. График |y| = | lg x2| (рис. 2.19) получается из графика функции y = lg x2, изображенного ранее на рис. 2.16.
90
