
MMATAN01
.pdf
1.9. Нормированное пространство
Определение 1.42. Линейное пространство X называется нормированным пространством, если в нем определена функция
x : X → R,
ставящая каждому элементу x X в соответствие действительное число x , называемое нормой элемента x, и норма удовлетворяет следующим аксиомам нормы
N1. x ≥ 0 и x = 0 x = θ.
N2. x + y ≤ x + y .
N3. αx = |α| x , α R.
П р и м е р ы
1) R — нормированное пространство. Если x R, то
x = |x| =
x, если x ≥ 0
−x, если x < 0.
Чтобы доказать это, достаточно проверить выполнение аксиом нормы:
N1. Очевидно, что |x| ≥ 0 и |x| = 0 x = 0.
N2. Сложив почленно два очевидных неравенства
−|x| ≤ x ≤ |x|,
−|y| ≤ y ≤ |y|,
получим
−(|x| + |y|) ≤ x + y ≤ |x| + |y| |x + y| ≤ |x| + |y|.
N3. |αx| = |α||x| устанавливается так:
√ √
|αx| = (αx)2 = α2 x2 = |α||x|.
41

2) Совокупность ограниченных функций f : [a, b] → R c нормой, введенной по формуле
f (x) = sup |f (x)|,
x [a,b]
образует нормированное пространство. Проверим аксиомы нормы:
N1. Очевидно, что f (x) ≥ 0 и f (x) = 0 тогда и только тогда, когда f (x) ≡ 0.
N2. Вторая аксиома следует из неравенства
|f (x) + g(x)| ≤ |f (x)| + |g(x)|.
N3. Третья аксиома следует из равенства
|αf (x)| = |α||f (x)|.
Количество примеров нормированных пространств позволяет расширить следующая теорема.
Теорема 1.8
Пространство со скалярным произведением будет нормированным пространством, если ввести в нем норму элемента x X по формуле
x = (x, x).
Д о к а з а т е л ь с т в о. Используя аксиомы S1 − S4 скалярного произведения, проверим аксиомы нормы:
N1. x = (x, x) ≥ 0 — очевидно;
x = (x, x) = 0 (x, x) = 0 x = θ.
N2. Для доказательства второй аксиомы, x + y ≤ x + y , установим сначала неравенство Шварца, которое также называют неравенством Коши—Буняковского
|(x, y)| ≤ x · y .
42
Для любых действительных t имеем
(tx + y, tx + y) ≥ 0.
С другой стороны, получаем
(tx+ y, tx+ y) = t2(x, x)+ 2t(x, y)+ (y, y) = x 2t2 + 2(x, y)t+ y 2.
Квадратный (относительно t R) трехчлен
x 2t2 + 2(x, y)t + y 2 ≥ 0
для любых t. Это возможно, если его дискриминант
D = 4(x, y)2 − 4 x 2 y 2 ≤ 0.
Откуда
(x, y)2 ≤ x 2 y 2 (x, y)2 ≤ x · y |(x, y)| ≤ x · y .
Докажем теперь неравенство x + y ≤ x + y :
x + y 2 = (x + y, x + y) = (x, x) + 2(x, y) + (y, y) =
= x 2 + 2(x, y) + y 2 ≤ x 2 + 2|(x, y)| + y 2 ≤
≤ x 2 + 2 x · y + y 2 = ( x + y )2.
Из только что установленного неравенства x+y 2 ≤ ( x + y )2 получаем
x + y ≤ x + y .
N3. αx = (αx, αx) = α2(x, x) = |α| (x, x) = |α| · x .
Из этой теоремы в частности следует, что Rk — нормированное пространство, так как это пространство со скалярным произведением и норма в нем введена по формуле
x = (x, x).
43
1.10. Метрическое пространство
Определение 1.43. Пусть X — множество любой природы. Функцию
d : X × X → R,
которую будем обозначать d(x, y) или dX (x, y), будем называть метрикой в множестве X, если она удовлетворяет аксиомам метрики
M1. d(x, y) ≥ 0 и d(x, y) = 0 x = y.
M2. d(x, y) = d(y, x).
M3. d(x, y) ≤ d(x, z) + d(z, y).
Множество X с введенной в нем метрикой d называется метрическим пространством и обозначается
(X, d) или (X, dX ).
Теорема 1.9
Нормированное пространство X будет метрическим пространством, если в нем ввести метрику по формуле
d(x, y) = x − y .
Д о к а з а т е л ь с т в о. Доказательство теоремы сводится к проверке аксиом метрики
M1. d(x, y) = x −y ≥ 0 и d(x, y) = x −y = 0 x −y = θ x = y.
M2. d(x, y) = x − y = (−1)(y − x) = |(−1)|y − x = d(y, x).
M3. d(x, y) = x − y = x − y + θ = x − y + z + (−z) = (x − z) + (z − y) ≤ x − z + z − y = d(x, z) + d(z, y).
П р и м е р ы
1) Из предыдущей теоремы следует, что множество действительных чисел R с метрикой
dR(x, y) = |x − y|
44
— метрическое пространство.
2) Множество Rk с метрикой |
|
|
dRk = x − y = |
k |
(xi − yi)2 21 |
|
i |
|
|
=1 |
|
также метрическое пространство.
3) Множество непрерывных функций f : [a, b] → R с метрикой
d(f, g) = sup |f (x) − g(x)|
x [a,b]
—метрическое пространство. Проверим аксиомы метрики:
M1. d(f, g) ≥ 0 — очевидно;
d(f, g) = 0 sup |f (x) − g(x)| = 0
x [a,b]
|f (x) − g(x)| ≡ 0 f (x) ≡ g(x).
M2. Так как |f (x) − g(x)| ≡ |g(x) − f (x)|, то
d(f, g) = sup |f (x) − g(x)| = sup |g(x) − f (x)| = d(g, f ).
x [a,b] |
x [a,b] |
|
M3. Имеем для любых x [a, b] |
|
|
|
|f (x) − g(x)| = |
|
= |(f (x) − h(x)) + (h(x) − g(x))| ≤ |f (x) − h(x)| + |h(x) − g(x)|. |
||
Откуда |
|
|
sup |f (x) − g(x)| ≤ |
sup |f (x) − h(x)| + |
sup |h(x) − g(x)| |
x [a,b] |
x [a,b] |
x [a,b] |
или, что то же самое,
d(f, g) ≤ d(f, h) + d(h, g).
45

4) Множество натуральных чисел N с введенной в нем метрикой
dN = d(m, n) = |m − n| mn
— метрическое пространство. Установим это, проверив аксиомы метрики:
M1. Выполнение первой аксиомы метрики очевидно. |
|
|
|||||||||||||||||||||
M2. Вторая аксиома также выполняется |
|
|
|
|
|
|
|
||||||||||||||||
d(m, n) = |
|m − n| |
= |
|n − m| |
= d(n, m). |
|
|
|||||||||||||||||
|
|
|
|
|
mn |
|
|
|
nm |
|
|
|
|
|
|
|
|||||||
M3. Путем последовательных преобразований получаем |
|
= |
|||||||||||||||||||||
m − n = m − n + k |
|
− |
|
k = |
|
k |
− n + m − k |
||||||||||||||||
|
mn |
|
|
|
|
mn |
mn |
|
|
|
|
mn |
|
||||||||||
|
|
n |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|||||
= |
|
(m − k) + |
|
|
(k |
− n). |
|
|
|||||||||||||||
k |
k |
|
|
||||||||||||||||||||
Откуда |
|
|
|
n |
|
|
|
|
|
|
m |
|
|
||||||||||
|m − n| ≤ |
|
|
|
|
|
+ |
|
|
|||||||||||||||
|
|
|m − k| |
|
|
|k − n|. |
|
|
||||||||||||||||
|
k |
k |
|
|
|||||||||||||||||||
Поделим последнее неравенство на mn |
|
|
|||||||||||||||||||||
|m − n| |
|
≤ |
|m − k| |
|
+ |
|k − n| |
, |
|
|
||||||||||||||
mn |
|
|
|
mk |
|
|
|
|
|
kn |
|
|
|||||||||||
аэто означает, что d(m, n) ≤ d(m, k) + d(k, n).
За м е ч а н и е. В множестве X метрику можно ввести, вообще говоря, несколькими способами. При этом получим разные метриче-
ские пространства. Например, (N, dR) и (N, dN) — различные метрические пространства.
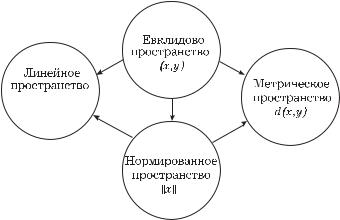
На рисунке 1.19 показаны связи, которые существуют или которые можно установить (введением нормы, метрики), между изучаемыми пространствами.
Заметим, наконец, что пространства Rk , и в частности R1 = R, одновременно являются линейными, евклидовыми, нормированными и метрическими пространствами.
46
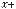
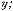 λ
λ
Рис. 1.19. Связь между пространствами
1.11. Основные понятия в метрическом пространстве
Для иллюстраций понятий, которые мы введем в этом пункте, используем плоскость (пространство R2).
Пусть (X, d) — метрическое пространство, т.е. множество X с введенной в нем метрикой d.
Определение 1.44. Элементы x X метрического пространства будем называть точками в метрическом пространстве, а число d(x, y) — р а с с т о я н и е м от точки x до точки y.
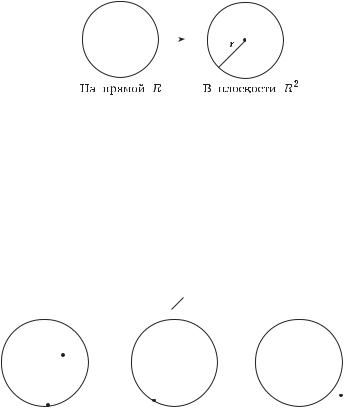
Определение 1.45. О к р е с т н о с т ь ю Or (q) точки q X радиуса r называют множество всех точек p X, таких, что
d(p, q) < r,
Or (q) = {p X : d(p, q) < r}.
47
;y











 ;y
;y
Рис. 1.17. Примеры окрестностей
Определение 1.46. Пусть E — некоторое множество метрического пространства X. Точка q X называется п р е д е л ь н о й точкой множества E, если любая ее окрестность содержит хотя бы одну точку p E, такую,что p = q.
Предельная точка может как принадлежать множеству E, так и не принадлежать E.
q |
|
|
предельная |
q |
|
предельная |
q |
|
изолированная |
q |
|
|
|||||||
|
E |
|
|
q E |
|
|
|
||
|
|
|
E q |
|
|
E |
|
|
E |
|
|
|
q |
q |
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.18. Предельные и изолированные точки
Определение 1.47. Если q E и q не является предельной для множества E, то q называется и з о л и р о в а н н о й точкой множества E.
Иными словами, точка q E X является изолированной точкой множества E, если можно указать окрестность точки q, в которой не содержится других точек из E.
48
Определение 1.48. Множество E метрического пространства X называется з а м к н у т ы м, если все его предельные точки принадлежат этому множеству.
Определение 1.49. Точка p называется в н у т р е н н е й точкой множества E, если она принадлежит множеству E вместе с некоторой окрестностью.
Определение 1.50. Множество E называется о т к р ы т ы м в X, если все его точки внутренние.
|
|
|
|
|
y |
|
|
|
|
|
( |
( |
) |
) |
x |
|
( |
|
|
) |
x |
a |
|
p |
b |
|
a |
|
p |
b |
||
E=(a,b) |
|
открытое в R |
|
E=(a,b) |
|
не открытое в R2 |
||||
|
|
|||||||||
|
|
|
||||||||
Рис. 1.19. Открытое множество
П р и м е р ы
1) Интервал (a, b) — открытое множество в R, но не является
открытым в R2 (рис. 1.19). |
|
|
|
|
|
|
|
||
2) Множество E = |
(x, y) R2 : x2 + y2 < 1 |
|
— открытое в R2. |
||||||
3) Замкнутое |
множество E = (x, y) |
|
R2 : x2 |
+ y2 |
|
1 не явля- |
|||
|
|
|
|
|
|
|
≤ |
|
|
ется открытым в R2. |
|
|
|
|
|
||||
4) Множество E = R — замкнутое и одновременно открытое в R.
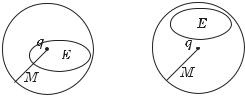
Определение 1.51. Множество E метрического пространства X называется о г р а н и ч е н н ы м множеством, если
( M > 0)( q X)( p E) : d(p, q) ≤ M.
При этом точка q может принадлежать E, а может и не принадлежать этому множеству.
49
y;
Рис. 1.20. Ограниченное множество
Если X — нормированное пространство, то множество E из X ограниченно тогда и только тогда, когда
( M1 > 0)( q X)( p E) : p − q ≤ M1.
В силу аксиом нормированного пространства при фиксированном q
p = p − q + q ≤ p − q + q ≤ M1 + q = M.
Откуда приходим к обычно применяемому определению для нормированного пространства.
Определение 1.52. Множество E нормированного пространства называется ограниченным, если
( M > 0)( p E) : p ≤ M.
В частности, отсюда следует, что множество E R — ограничено, если
( M > 0)( x E) : |x| ≤ M.
В заключение этого пункта докажем следующую важную теорему (ответ на вопрос, поставленный в п. 1.4.4).
Теорема 1.10
Пусть E — замкнутое множество из R, ограниченное сверху (снизу). Пусть y = sup E (y = inf E). Тогда y E.
50
