MMATAN04

Министерство образования и науки РФ

Нижегородский государственный университет им. Н.И. Лобачевского

Национальный исследовательский университет

В.Н. Кошелев, Б.В. Лисин

ДИФФЕРЕНЦИРОВАНИЕ. ИССЛЕДОВАНИЕ ФУНКЦИИ

Учебное пособие

Рекомендовано ученым советом радиофизического факультета для студентов ННГУ, обучающихся по специальностям 010801 «Радиофизика и электроника»,

090106 «Информационная безопасность телекоммуникационных систем»

Нижний Новгород Издательство Нижегородского госуниверситета

2011

УДК 517.1 ББК В22.161.1 К 76

Рецензенты:

В.Н. Белых — доктор физ.-мат. наук, профессор В.И. Сумин — доктор физ.-мат. наук, профессор

К 76 Кошелев В.Н., Лисин Б.В. Дифференцирование. Исследование функции: Учебное пособие. — Нижний Новгород:

Изд-во Нижегородского госуниверситета, 2011. — 183 с.

ISBN 978-5-91326-006-2

В основе настоящего пособия лежат лекции, читаемые студентам радиофизического факультета Нижегородского государственного университета. В первой главе излагаются теоретические основы дифференциального исчисления функции одной переменной. Во второй главе изучаются основные понятия, необходимые для исследования функции, и приводится схема исследования функции одной переменной. Третья глава носит практический характер. Она разбита на отдельные занятия, в которых приводятся задачи с их подробным решением. Пособие построено таким образом, что позволяет самостоятельно изучать изложенный материал.

Для студентов физических факультетов университетов.

Ответственный за выпуск:

председатель методической комиссии радиофизического факультета, д. ф.-м. н., профессор В.Н. Мануилов

c Кошелев В.Н., Лисин Б.В., 2011c Нижегородский государственный

университет им. Н.И. Лобачевского, 2011

Оглавление

ГЛАВА 1. Дифференцирование функции одной переменной . . . . . . . . . . . . . . . . . . . . . . . . 5

1.1. Определение производных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 1.2. Геометрический смысл производных . . . . . . . . . . . . . . . . . . . . . . . . 8 1.3. Дифференцируемые функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.4. Правила вычисления производных . . . . . . . . . . . . . . . . . . . . . . . . 13 1.5. Дифференциал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 1.6. Основные теоремы дифференциального исчисления . . . . . . 19 1.7. Производные и дифференциалы высших порядков . . . . . . . . 23

ГЛАВА 2. Исследование функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 2.1. Правило Лопиталя . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 2.2. Формула Тейлора . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.3. Разложение основных функций по формуле Тейлора . . . . . 35 2.4. Условия монотонности функции . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 2.5. Экстремумы функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 2.6. Выпуклые и вогнутые функции . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 2.7. Выпуклые и вогнутые кривые . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 2.8. Асимптоты графика функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 2.9. Схема исследования функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

ГЛАВА 3. Практика по темам «Дифференцирование и исследование функции» . . . . . . . . . . . . . . . . . . . . . . . . 53

Занятие 1. Дифференцирование суммы, произведения и частного . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53

Занятие 2. Дифференцирование сложной функции . . . . . . . . . . . . . . 62 Занятие 3. Производная явной функции . . . . . . . . . . . . . . . . . . . . . . . . . 67 Занятие 4. Дифференцирование явной функций . . . . . . . . . . . . . . . . . 72

Занятие 5. Производная обратной, заданной параметрически и неявной функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79

Занятие 6. Дифференциал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 Занятие 7. Повторное дифференцирование . . . . . . . . . . . . . . . . . . . . . . 92 Занятие 8. Производные и дифференциалы высших порядков . . 99 Занятие 9. Правило Лопиталя . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106 Занятие 10. Формула Тейлора . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 Занятие 11. Приложения производных . . . . . . . . . . . . . . . . . . . . . . . . . 116 Занятие 12. Задачи на максимум и минимум . . . . . . . . . . . . . . . . . . . 125 Занятие 13. Исследование рациональных функций . . . . . . . . . . . . 131 Занятие 14. Исследование иррациональных функций . . . . . . . . . 146 Занятие 15. Исследование тригонометрических функций . . . . . . 157 Занятие 16. Исследование функций в параметрической форме 171

Графики функций задач для самостоятельной работы (занятия 13-16) . . . . . . . . . . . . . . . . . . . . . . . . . . . 179

Глава 1

Дифференцирование функции одной переменной

1.1. Определение производных

Определение 1.1. Пусть f : (a, b) → R — функция действительной переменной. Взяв произвольную точку x0 (a, b), составим отношение

называют производной от функции f (x) в точке x0.

b) Предел

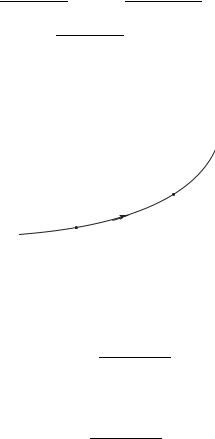
3) Пусть по кривой C движется материальная точка. За время t0 она прошла путь S(t0), за время t — путь S(t) (рис. 1.1).

C

S(t)

S(t )

0

Рис. 1.1. К физической интерпретации производной

Средняя скорость этой точки за промежуток времени от t0 до t

равна

vср = S(t) − S(t0) . t − t0

Если производная S (t0) существует, то мгновенная скорость материальной точки в момент t0 равна значению этой производной

З а м е ч а н и е. Определение a) производной, как показывают приведенные примеры, наиболее естественное. Его удобно применять на практике. Тем не менее существует и другое (эквивалентное) определение, которое обычно используют при доказательстве различных теорем.

7

Если в последнем определении производной положить x = t, то получаем также часто используемое определение производной

1.2. Геометрический смысл производных

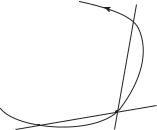
Определение 1.2. Кривая L называется ориентированной кривой, если на ней задан обход. Если при обходе точка M следует за точкой M0, то будем говорить, что M находится справа от M0. Если при обходе точка M предшествует точке M0, то будем говорить, что M находится слева от точки M0.

L M(справа)

M0

M(слева)

Рис. 1.2. Ориентированная кривая

8

Обычно направление обхода (если нет других оговорок) определяется возрастанием параметра t, если кривая задана параметрически x = x(t), y = y(t), t0 ≤ t ≤ T , или возрастанием независимой переменной x, если кривая задана в явном виде y = f (x), a ≤ x ≤ b.

L

M 1

M 0

M 2

Рис. 1.3. К определению касательных

Определение 1.3. Пусть M1 — любая точка ориентированной кривой L, лежащая справа от точки M0, и M2 — любая точка кривой L, лежащая слева от точки M0. Рассмотрим секущие M0M1 и M0M2.

a)Правосторонней касательной к кривой L в точке M0 называется предельное положение секущей M0M1, когда точка M1 стремится вдоль по кривой к точке M0 (оставаясь справа от M0).

b)Левосторонней касательной к кривой L в точке M0 называется предельное положение секущей M0M2, когда точка M2 стремится вдоль по кривой к точке M0 (оставаясь слева от M0).

c)Если левосторонняя и правосторонняя касательные в точке M0 совпадают, то такая прямая называется касательной к кривой L в точке M0.

d)Если левосторонняя и правосторонняя касательные в точке M0 не совпадают, то точка M0 называется угловой точкой.

9

αϕ

Рис. 1.4. Геометрический смысл производной

Пусть f : (a, b) → R и в точке x0 (a, b) существует конечная производная f (x0).

Имеем tg ϕ = f (x0) (рис. 1.4). Используя непрерывность функ- x

ции tg x, получаем

т.е. f (x0) — тангенс угла наклона касательной к кривой y = f (x), проведенной в точке (x0, f (x0)).

Аналогично f+(x0) и f−(x0) — тангенсы углов наклона правосторонней и левосторонней касательных.

Если f (x0), f+(x0) или f−(x0) бесконечные производные, то соответствующие касательные параллельны оси y.

На рис. 1.5 приведены примеры односторонних касательных и касательных, иллюстрирующих бесконечные производные.

Легко видеть, что уравнение касательной, проходящей через точку (x0, f (x0)), к кривой y = f (x) имеет вид

y = f (x0) + f (x0)(x − x0).

10