
MMATAN04
.pdf
2. a) Для функции y = x+ln x (x > 0) существует обратная функция x = x(y), так как производная прямой функции всегда положитель-
на: |
|
1 |
|
x + 1 |
|
|
y |
= 1 + |
= |
> 0 при x > 0. |
|||
|
|
|||||
x |
|
x |
|
x |
||
|
|
|
||||
Область существования (определения) обратной функции совпадает с областью изменения прямой функции. В нашем случае обратная функция x = x(y) определена при −∞ < y < +∞. Ее производная
равна |
1 |
|
x |
|
|
x = |
= |
. |
|||
yx |
x + 1 |
||||
y |
|
|
|||
|
|
|
|
б) Для функции y = sh x существует обратная функция x = x(y),
так как yx = ch x > 0. Область существования обратной функции: |
||||||||||||
−∞ < y < +∞. |
|
1 |
|
1 |
|
1 |
|
1 |
|
|||
x |
= |
= |
= |
= |
. |
|||||||
|
|
|
|
|
|
|||||||
y |
|
yx |
|
ch x |
|
√1 + sh 2x |
|
1 + y2 |
||||
3. У дифференцируемой функции y = y(x) однозначные непрерывные ветви обратных функций x = x(y) существуют только на участках монотонности прямой функции y = y(x). Поэтому ищем участки знакопостоянства производной для y = 2x2 − x4
y = 4x − 4x3 = −4(x + 1)x(x − 1).
Легко видеть, что y > 0 на интервалах (−∞, −1) и (0, 1); y < 0 на интервалах (−1, 0) и (1, +∞). Таким образом, функция y = 2x2 − x4 имеет четыре однозначные непрерывные ветви обратных функций. Чтобы легче найти эти ветви, построим график прямой функции (рис. 3.1).
Решая уравнение
y = 2x2 − x4
относительно x, получаем
x4 − 2x2 − y = 0, x2 = 1 ± 1 − y,
x = ± 1 + 1 − y, x = ± 1 − 1 − y.
81

y 
1
1 0 1 x
Рис. 3.1. График функции y = 2x2 − x4
После этого нетрудно выделить однозначные непрерывные ветви обратных функций x = x(y), соответствующие участкам монотонности прямой функции (на графике слева направо).
1 |
ветвь: −∞ < y ≤ 1, |
x1 = − |
1 + √ |
|
|
|
|
|
|||||||||
1 − y. |
|||||||||||||||||
2 |
ветвь: 0 ≤ y ≤ 1, |
x2 |
= − |
1 − √ |
|
|
|
|
|
||||||||
1 − y. |
|||||||||||||||||
3 |
ветвь: 0 ≤ y ≤ 1, |
x3 |
= |
1 − √ |
|
|
|
|
|
||||||||
1 − y. |
|||||||||||||||||
4 |
ветвь: −∞ < y ≤ 1, |
x4 = |
1 + √ |
|
|
|
|||||||||||
1 − y. |
|||||||||||||||||
|
Производные обратных функций равны: |
||||||||||||||||
|
|
xi = |
|
1 |
|
|
|
|
|
(i = 1, 2, 3, 4). |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
4x(1 |
− x2) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. Если функция y = y(x) задана параметрически посредством параметра t
x = x(t), y = y(t),
то производная yx может быть найдена по формуле
yx = yt
xt
82
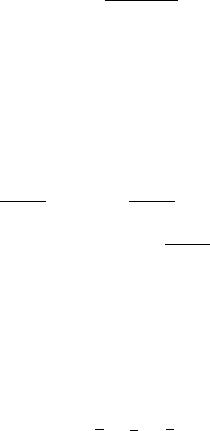
и также задается параметрически |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = x(t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx = yx(t). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = sin2 t, |
|
|||||
Для функции y(x), заданной параметрически y = cos2 t, |
имеем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
= |
y |
|
|
= |
|
− |
2 cos t sin t |
= |
|
|
|
1. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
2 sin t cos t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. x = a ch t, |
|
|
|
y = b sh t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
b ch t |
|
= |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
yx = |
|
|
|
|
t |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cth t. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a sh t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xt |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6. x = a(t − sin t), |
y = a(1 − cos t). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
a sin t |
|
|
|
|
|
|
|
|
2 sin |
t |
|
cos |
|
t |
|
|
|
|
|
t |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
y |
|
= |
|
|
t |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
= ctg |
|
. |
|
||||||||||||||||||
|
x |
|
a(1 |
|
|
|
|
cos t) |
|
|
|
|
|
|
|
|
|
|
|
|
2 t |
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
2 sin |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
7. x = arcsin |
|
√ |
|
|
t |
|
, |
|
y = arccos |
√ |
|
|
|
|
1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
1 + t2 |
|
1 + t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 + t |
2 |
− |
√ |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
x |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + t2 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 + t2 , |
|
|||||||||
t |
|
|
|
|
1 − |
|
t2 |
|
|
|
· |
|
|
|
|
|
|
|
|
|
1 + t2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
1 + t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
yt = |
− |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
− |
|
|
|
|
1 |
|
|
|
|
√ |
|
|
|
|
|
t |
|
|
|
= |
|
t |
|
|
, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + t2 |
|
|
t (1 + t2) |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 + t2 |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|||||||||||||||
|
|
|
|
1 + t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
y |
= |
|
t |
|
|
|
|
= sign t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
t |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8. Дифференцируя обе части уравнения
√ √ √
x + y = a
83

по x в предположении, что y = y(x), получаем
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = − |
y |
|
|
|||||||
|
|
2√ |
|
|
+ |
|
|
|
· y = 0 |
|
. |
|
|
|
|||
|
|
2√ |
|
|
x |
|
|
||||||||||
|
|
x |
|
|
|
||||||||||||
|
|
|
y |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
9. Дифференцируя по x уравнение x 3 + y 3 |
= a 3 |
, получаем |
|||||||||||||||
3 |
|
x−3 |
+ y · y−3 = 0 y = − 3 |
x . |
|||||||||||||
2 |
|
1 |
|
|
|
|
1 |
|
|
|
y |
||||||
y1
10.Дифференцируем уравнение arctg x = 2 ln(x2 + y2)
|
|
|
|
|
|
1 |
|
|
|
|
|
y x − y |
= |
x + yy |
, |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 + |
y2 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y |
||||||||
y x − y = x + yy , y (x − y) = x + y, y = |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||
x |
− |
y |
||||||||||||||||||||||||||||||||||||||||
11. Из уравнения r = aϕ следует rx = aϕx, где |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
r |
= |
|
x + yy |
|
|
= |
|
x + yy |
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
ϕ |
= |
1 |
|
|
|
|
|
|
y x − y |
= |
y x − y |
. |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
x |
|
1 + |
y2 |
|
|
|
x2 |
|
|
|
r2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Путем последовательных преобразований получаем: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rx = aϕx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x + yy |
= a |
y x − y |
, |
|
rx + ryy = ay x |
− |
ay, |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
r |
|
|
|
|
r2 |
|
|
|
|
y |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
rx + ay |
|
|
|
|
|
|
|
+ |
|
|
tg ϕ + ϕ |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
= |
|
|
|
|||||||||||||||||||||||||
|
y = |
= |
|
|
|
|
x |
a |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
ax − ry |
|
|
1 − |
r |
· |
|
|
1 − ϕ tg ϕ |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
a |
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= |
|
tg ϕ + tg ( arctg ϕ) |
|
|
= tg (ϕ + arctg ϕ). |
|
|
|
||||||||||||||||||||||||||||||||||
|
1 − tg ϕ tg ( arctg ϕ) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Задачи для самостоятельной работы
5.1.Показать, что существует однозначная функция y = y(x), определяемая уравнением
x = y − ε sin y (0 ≤ ε < 1),
и найти производную yx.
5.2.Найти область существования обратной функции x = x(y) и найти ее производную, если
y= x + ex.
5.3.Выделить однозначные непрерывные ветви обратной функции x = x(y), найти их производные, если
x2
y = 1 + x2 .
Построить график.
Найти производные yx от функций, заданных параметрически:
3 |
|
|
|
|
|
3 |
|
|
|
|
√t, y = 1 |
|
|||||||
5.4. x = 1 − |
− √t. |
||||||||
5.5. x = a cos t, |
|
y = b sin t. |
|
|
|
|
|||
5.6. x = a cos3 t, |
|
y = a sin3 t. |
|||||||
Найти производные yx от следующих функций, заданных в неяв-
ном виде: |
|
5.7. y3 − 3y + 2ax = 0. |
5.8. y2 − 2xy + b2 = 0. |
5.9. sin(xy) + cos(xy) = tg (x + y). 5.10. x − y = arcsin x − arcsin y.
5.11. Найти yx, если
где r =
85

Ответы
5.1. |
|
x |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
5.2. |
−∞ |
|
|
|
+ |
∞, |
|
|
|
y |
|
1 |
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
ε cos y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y . |
||||||||||||||||||||||||||||
|
y |
= |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< y < |
|
|
|
|
x = |
|
− |
|
|
|
|
|
|
||||||||||||||||
5.3. |
|
|
|
|
|
|
|
|
1 − y |
|
|
(0 ≤ y < 1); |
|
|
x2 = |
|
1 − y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x1 = − |
|
|
|
|
|
|
|
(0 ≤ y < 1). |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t(1 |
|
|
|
√ |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−a |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
√t)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5.4. |
6 |
|
(1 |
− |
|
|
|
t) |
|
|
(t > 0, t |
= 1). |
5.5. |
y |
= |
|
b |
ctg t. 5.6. y |
= |
|
|
tg t. |
|||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
y cos2(x + y)(cos(xy) − sin(xy)) − 1 |
|||||||||||||||||||||||||||
5.7. |
|
|
|
|
|
|
. 5.8. |
|
|
|
|
|
|
|
5.9. − |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||
3(1 |
|
|
|
y2) |
y |
|
x |
x cos2(x + y)(cos(xy) |
|
sin(xy)) |
|
|
1 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
− |
|
|
|
2 |
|
|
|
|
|
|
|
√ |
|
− |
|
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
− |
|
|
|
|
|
|
− |
|
|
|||||||||
|
|
1 − y |
(1 − |
|
|
|
1 − x |
|
|
|
|
ϕ + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
|
x |
(1 |
|
|
|
|
|
1 |
|
|
y |
) |
. 5.11. tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
5.10. √ |
|
|
|
|
|
2 |
|
|
|
|
|
|
− |
|
|
|
− |
2 |
|
|
|
|
arctg m . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Занятие 6. Дифференциал
Напомним определение дифференциала. Пусть функция
f : (a, b) → R
дифференцируема в точке x0 (a, b). Тогда ее приращение в этой точке представимо в виде
f (x0) = A · x + α(Δx) · x,
A — постоянное число, α(Δx) — бесконечно малая при x → 0. Выражение A · x называется дифференциалом функции f (x) в
точке x0 и обозначается
df (x0) = A · x.
В частности из этого определения следует, что если x — независимая переменная, то x = dx. Формула для вычисления дифференциала имеет вид
d f (x) = f (x) dx.
86

Задание
1. Для функции
f (x) = x3 − 2x + 1
определить: 1) f (1); 2) df (1) и сравнить их, если:
а) x = 1; б) x = 0,1; в) x = 0, 01.
Найти дифференциал функции y, если
2. y = arcctg (2 tg x).
4. y = a1 arctg xa .
Найти
√
6. d( a2 + t2).
3. |
y = ln |x + |
√ |
|
|
|
||||
2 |
2 |
|. |
|||||||
x |
+ a |
||||||||
5. |
|
2a |
ln |
x + a . |
|
||||
|
y = 1 |
|
x − a |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. d(sin ϕ − ϕ cos ϕ).
Пусть u, v — дифференцируемые функции. Найти дифференциал функции y, если:
|
|
|
|
|
1 |
|
|
9. |
y = arctg |
u |
|||||
8. y = |
√ |
|
|
|
|
|
. |
|
. |
||||||
|
|
|
|
|
v |
||||||||||
u |
2 |
+ v |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найти |
|
|
|
|
|
|
|
|
|
|
|
||||
10. |
d |
(x3 − 2x6 − x9). |
11. |
|
d(sin x) |
||||||||||
|
|
|
. |
||||||||||||
d(x3) |
|||||||||||||||
|
d(cos x) |
||||||||||||||
Заменяя приращение функции дифференциалом, найти приближенно следующие значения:
12. |
√1, 02. |
13. sin 151 |
o |
. |
||
|
3 |
|
|
|
|
|
87
Решения
1. Приращение функции f (x) в точке x0 вычисляется по формуле
f (x0) = f (x) − f (x0).
Если ввести приращение аргумента x = x − x0, то x = x0 + x и приращение функции равно
f (x0) = f (x0 + x) − f (x0).
Для функции f (x) = x3 − 2x + 1 имеем
f (1) = f (1 + x) − f (1) = (1 + x)3 − 2(1 + x) + 1 − (1 − 2 + 1)
или после несложных преобразований
f (1) = x + 3(Δx)2 + (Δx)3.
Вычисляем дифференциал функции в точке x = 1
df (1) = f (1) dx = (3x2 − 2x) x=1dx = dx. |
|
|
|
|
|
Откуда с учетом того, что для независимой |
переменной x = dx, |
получаем |
|
df (1) = x. |
|
Теперь вычисляем значения приращения функции f (x) и ее диф-
ференциала для различных значений x: |
|
|
|||
а) |
x = 1; |
f (1) |
= 5; |
df (1) |
= 1; |
б) |
x = 0, 1; |
f (1) |
= 0, 131; |
df (1) |
= 0, 1; |
в) |
x = 0, 01; |
f (1) |
= 0, 010301; |
df (1) |
= 0, 01. |
Сравнения показывают, что чем меньше по абсолютной величине приращение аргумента, тем менее отличаются друг от друга значения приращения функции и дифференциала.
2. dy = ( arcctg (2 tg x)) dx = |
1 |
|
1 |
dx = |
dx |
|
|
· |
|
|
. |
||
1 + 4 tg 2x |
cos2 x |
1 + 3 sin2 x |
||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
3. dy = (ln |x + √x2 + a2|) dx = |
|
|
|
|
|
|
|
|
|
1 + |
dx = |
|||||||||||||||||||||||||||||||||||||
x + √ |
|
|
|
|
|
|
√ |
|
||||||||||||||||||||||||||||||||||||||||
x2 + a2 |
|
x2 + a2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
= |
√ |
|
|
dx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
2 |
+ a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
x |
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||||||||||
4. dy = |
|
arctg |
|
dx = |
|
· |
|
|
|
|
|
|
|
· |
|
|
dx |
= |
|
|
. |
|
||||||||||||||||||||||||||
a |
a |
a |
|
1 + |
x2 |
|
a |
x2 + a2 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Используя свойства логарифмов, запишем |
|
| |
| |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y = |
|
2a |
ln |
x + a |
|
|
|
2a |
| − |
a |
| − |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x − a |
|
= 1 (ln x |
|
|
|
|
ln x |
+ a ). |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
dy = |
|
|
|
|
|
|
|
− |
|
|
|
dx |
= |
|
. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2a |
x − a |
x + a |
x2 − a2 |
|
|||||||||||||||||||||||||||||||||
6. d(√ |
|
) = √ |
|
t dt = |
√ |
t |
dt. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
a2 + t2 |
a2 + t2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
a2 + t2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
7. |
d(sin ϕ |
− |
ϕ cos ϕ) = (sin ϕ |
− |
ϕ cos ϕ) dϕ = ϕ sin ϕ dϕ |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
. |
|
||||||||||||||
8. При решении этого и следующего примеров используются правила дифференцирования в дифференциалах:
1) |
d(u + v) = du + dv; |
2) |
d(uv) = v du + u dv; |
|
|||||
3) |
d(cu) = c du, c = const; |
4) |
d |
|
u |
|
= v du − u dv |
; |
|
|
|
|
v |
|
v2 |
||||
5)df (u(x)) = fu · du. Итак, имеем
d |
|
|
1 |
|
|
= |
|
|
|
|
|
|
1 |
|
|
|
|
d(u2 + v2) = |
− |
u du + v dv |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
√u2 + v2 |
−2 (u2 + v2)3 |
|
|
|
|
|
(u2 + v2) 2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
9. dy = d |
arctg |
u |
= |
|
1 |
|
|
|
|
d |
|
u |
|
= |
|
v2 |
|
v du − u dv |
= |
|||||||
v |
|
1 + uv2 |
· |
v |
u2 |
+ v2 · |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
v2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
=v du − u dv . u2 + v2
89

d
Производная d g(x) f (x) от функции f (x) по переменной g(x) находится как отношение дифференциалов d f (x) и d g(x).
10. |
|
|
|
|
|
|
|
|
|
d(x3 − 2x6 − x9) |
|
(3x2 − 12x5 − 9x8) dx |
|
|||||||
|
d |
|
(x3 |
− |
2x6 |
− |
x9) = |
= |
= |
|||||||||||
|
d(x3) |
|
|
3x2 dx |
||||||||||||||||
|
|
|
|
|
|
|
|
|
d(x3) |
|
|
|
||||||||
= |
3x2 − 12x5 − 9x8 |
= 1 |
− |
4x3 |
− |
3x6 |
. |
|
|
|
||||||||||
|
|
|
|
|
3x2 |
|
|
|
|
|
|
|
|
|
||||||
11. |
d(sin x) |
= |
cos x dx |
|
= − ctg x. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
d(cos x) |
− sin x dx |
|
|
|
|
|||||||||||||||
12. При достаточно малых по абсолютной величине x приближенно выполняется равенство
f (x0) df (x0)
или
f (x) − f (x0) f (x0)(x − x0).
Полагая x0 = 0, получаем формулу приближенных вычислений для
малых x
f (x) f (0) + x f (0).
√
Чтобы найти приближенно 3 1, 02, рассмотрим функцию
√
f (x) = 3 1 + x,
где x = 0, 02. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
|
|
|
1 |
|
|
, |
|
f (0) = |
1 |
, f (0) = 1, |
||
|
|
|
|
|
|
|
|||||||
|
3 |
|
(1 + x)2 |
|
|
3 |
|
||||||
|
|
√1 + x 1 + 3 x, |
|
||||||||||
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
1, 02 1 + |
0, |
1, 0067. |
|||||||||
|
3 |
||||||||||||
13. Воспользуемся формулой приведения
sin 151o = sin(180o − 290) = sin 29o = sin π6 − 180π .
90
