2012_МА_часть_1_методические рекомендации

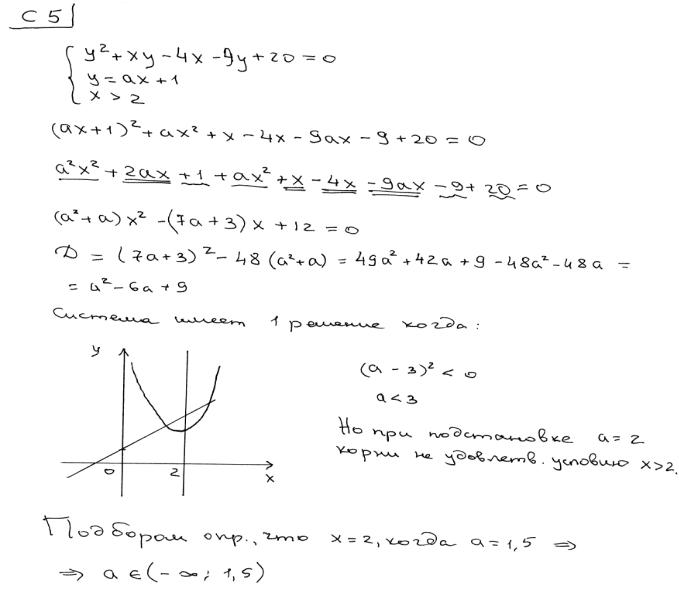
Пример 7.

Найдите все значения параметра a , при каждом из которых система

y 2 + xy −4x −9 y + 20 = 0,y = ax +1,

x > 2

имеет единственное решение.

Ответ. −1 < a ≤0, 1 ≤ a <1,5. (См. критерии задачи 4.)

Комментарий. Конец решения после вычисления дискриминанта полон крайне странными утверждениями, вроде «Система имеет одно решение,

когда (a −3) 2 < 0 », рассмотрения (почему-то?) a = 2 или x = 2 и т.п. Т.е. тут –

абсолютное непонимание ситуации. Но, тем не менее, до этого явно присутствует «…верное получение квадратного уравнения с параметром а относительно одной из переменных». Поэтому допустимо поставить 1 балл.

Оценка эксперта: 1 балл.

71

Пример 8.

Найдите все значения параметра a , при каждом из которых система

y 2 + xy −4x −9 y + 20 = 0,y = ax +1,

x > 2

имеет единственное решение.

Ответ. −1 < a ≤0, 1 ≤ a <1,5. (См. критерии задачи 4.)

72

Продолжение примера 8.

Комментарий. Что-то разумное есть, а по виду ответа можно поставить и 2 балла. Есть одно серьезное «но». При решении рациональных неравенств автор «избавляется» от знаменателей, не обращая внимания на их знак. Значит, ему просто повезло, что промежутки в его ответе имеют нужные концы. Найдены они необоснованно.

Оценка эксперта: 1 балл.

73

§6. Задания с развернутым ответом повышенного уровня сложности С6. Критерии проверки и оценки решений.

За 11 лет проведения ЕГЭ в нашей стране накопились различные статистические данные. Одним из самых устойчивых (11 раз проверенных на выборках почти из миллиона данных) показателей является процент решаемости (получение 4 или 3 баллов) последней по номеру задачи в вариантах КИМ. Этот процент ни по одному из вариантов КИМ никогда не превышал 2% и почти всегда был ниже 1%. В 2010 и 2011 гг. данные по С6 в целом по стране (июньский экзамен) выглядят так:

Подчеркнем, что это нормальное положение дел. Последняя задача в КИМ должна различить достижения выпускников, имеющих в целом самый высокий уровень подготовки. Процент ее решаемости и не должен превышать 1-2% по самому смыслу задания на этом месте.

С одной стороны, 1% - это всего один человек из, скажем, четырех выпускных классов конкретной школы. Но, с другой стороны, 0,5% от миллиона – это 5 тысяч человек, что с запасом перекрывает потребности всех элитных (по математике) вузов. Если увеличить 0,5%, скажем до 3%, то это уже 30 тысяч человек, у которых итоговые результаты по ЕГЭ будут в таком случае мало различимы. Другими словами, такое увеличение приведет к резкому снижению дифференцирующей составляющей КИМ на верхней границе шкалы распределения результатов.

Поэтому на часто задаваемые в качестве некоторых «обвинений» в адрес ЕГЭ вопросы типа «Как обычный ученик в среднем классе должен решать С6?» или «Как обычный школьный учитель должен организовать в своем классе подготовку к решению С6?», ответ один – «Систематические занятия математикой, начиная с 5 класса». Для сравнения, подставьте вместо «С6» в эти вопросы «вариант мехмата МГУ, матмеха ЛГУ, Физтеха и т.п». Ответ для такой подстановки представляется очевидным.

Содержательно, задание С6 проверяет в первую очередь не уровень математической (школьной) образованности, а уровень математической культуры. Вопрос формирования соответствующей культуры – вещь деликатная и, в целом, формируемая на протяжении нескольких лет.

В то же время, изменения в формате ЕГЭ связаны, в частности, с тем, что задание С6 по своему тематическому содержанию стало элементарнее, а для его решения, формально, достаточно простейших сведений типа «сумма нечетного числа нечетных слагаемых нечетна». По этой причине, например, в ЕГЭ-2010 более 10% участников приступали к решению задания С6: оно перестало отпугивать накрученностью своей формулировки. В ЕГЭ-

74

2011 к выполнению задания С6 приступало уже 12,7% участников. Грубо говоря, не очень подготовленный по синусам, логарифмам или технике дифференцирования ученик, обладающий нормальным здравым взглядом на вещи, достаточно спокойно может получить за С6 и 1 балл, и 2 балла.

Всвязи этим, хотелось бы подчеркнуть, что никаких фактов из теории чисел типа теоремы Вильсона, чисел Мерсенна, малой теоремы Ферма, теории сравнений и т.п. для решения заданий С6 не требуется. Тот, кто эти факты знает, разумеется, может их использовать, но, подчеркиваем, при решении всегда можно обойтись и без них.

В2010 году критерии оценивания выполнения задания С6, в самых общих чертах, были приближены к традиционно сложившейся системе оценивания олимпиадных задач. А именно, обоснованное получение верного ответа, то есть получение оценки «+» в олимпиадной терминологии, соответствует получению 4 баллов. Выставление 3 баллов за решение

задания С6 примерно соответствует олимпиадным оценкам « +(−) » или « +i »,

которые традиционно описываются словами «задача решена, но имеются мелкие замечания к решению». Двигаясь далее, количественные оценки в 2 балла и в 1 балл были аналогами качественных олимпиадных оценок « ± »

и« », которые довольно часто в словесной форме объясняют так: «имеется значительное продвижение в решении, но полное решение требует привлечения других идей» и «задача не решена, но подход к решению верен

инекоторые частные случаи разобраны верно».

Конкретная трактовка описанного соответствия зависела от конкретной задачи.

Задача 1 (ЕГЭ-2010).

Каждое из чисел 2, 3, …, 7 умножают на каждое из чисел 13, 14, …, 21 и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Решение.

1. Если все произведения взяты со знаком плюс, то их сумма максимальна и равна

2.Так как сумма оказалась нечетной, то число нечетных слагаемых в ней – нечетно, причем это свойство всей суммы не меняется при смене знака любого ее слагаемого. Поэтому любая из получающихся сумм будет нечетной, а значит, не будет равна 0.

3.Значение 1 сумма принимает, например, при такой расстановке знаков

упроизведений, которая получится при раскрытии следующих скобок:

(−2 +3 −4 +5 +6 −7)(−13 −14 −15 −16 +17 −18 +19 +20 +21) =1 1 =1.

Ответ: 1 и 4131.

75

Следующий пример взят из диагностических работ марта 2011 г., а его решение – более краткое, чем это было предложено в критериях проверки

Решение.

Если n =1 , то левая часть равна нулю, а правая – нет. Если n четно, то

и что k = 3 является корнем уравнения. Если k = 4 , то 5k −1 =125 > 6k +7 =31 . При каждом последующем увеличении k на 1 левая часть 5k −1 будет возрастать в

пять раз, а правая часть 6k +7 будет возрастать на 6. Значит, при k > 3 верно неравенство 5k −1 > 6k +7 .

Ответ: n = 5, k = 3 .

76

Задача 3 (ЕГЭ-2011).

Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 10 раз больше, либо в 10 раз меньше предыдущего. Сумма всех членов последовательности равна 3024.

а) Может ли последовательность состоять из двух членов? б) Может ли последовательность состоять из трёх членов?

в) Какое наибольшее количество членов может быть в последовательности?

Решение.

решений в натуральных числах. Поэтому последовательность не может состоять из двух членов.

б) Последовательность может состоять из трёх членов: 252, 2520, 252. в (пример) Приведём пример последовательности из 549 членов:

274

в(оценка) Допустим, что в последовательности более чем 549 членов. Разобьём первые 550 членов последовательности на 275 пар соседних членов: первый и второй, третий и четвёртый, пятый и шестой и т.д. Сумма двух членов в каждой паре делится на 11 и поэтому не меньше 11. Значит, сумма всех членов последовательности не меньше, чем 275 11 =3025 >3024 .

Противоречие.

Ответ: а) нет, б) да, в) 549.

Задача 4 (ЕГЭ-2011).

На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5 , среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно −18 .

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

Решение.

77

Пусть среди написанных чисел k положительных, l отрицательных и m нулей. Сумма набора чисел равна количеству чисел в этом наборе,

а) Заметим, что в левой части каждое слагаемое делится на 9, поэтому k +l + m — количество целых чисел — делится на 9. По условию 27 < k +l + m < 45 , поэтому k +l + m = 36 . Таким образом, написано 36 чисел.

б) Приведём равенство 9k −18l = −5(k +l +m) к виду 13l =14k +5m . Так как

m ≥ 0 , получаем, что 13l ≥14k , откуда l > k . Следовательно, отрицательных чисел больше, чем положительных.

чисел не более 16.

в(пример) Приведём пример, когда положительных чисел ровно 16. Пусть на доске 16 раз написано число 9, 18 раз написано число −18 и два

Ниже будут рассмотрены решения задач 1-4 и использоваться приведенные критерии. Как видно, критерии в 2011 г. стали структурно более формализованными. Их текст практически никак не использует тематическую или содержательную фабулу конкретной задачи. Такие изменения были предприняты для большей согласованности и унификации выставляемых экспертами оценок. Дело в том, что, как показала практика работы региональных комиссий, "олимпиадный" подход, ориентированный на шкалу оценок типа «+», « ± », « » и «-«, приводил к заметной неопределенности и излишнему разбросу в интерпретации того, что такое, скажем, «задача не решена, но подход к решению верен и некоторые частные случаи разобраны верно».

В ЕГЭ-2012 в основном также будут использованы именно жестко структурированные по пунктам задачи критерии.

78

Примеры оценивания заданий С6.

Пример 1

Каждое из чисел 2, 3, …, 7 умножают на каждое из чисел 13, 14, …, 21 и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Ответ: 1 и 4131. (См. критерии задачи 1.)

Комментарий.

Ситуация понятная. Решение, пожалуй, даже более ясное, чем приведенное выше. В нем конкретно указано и общее число (54) произведений, и число (15) нечетных произведений. Формально, выписанный ответ не совпадает с верным ответом. Но верный ответ обоснованно получен строчкой ранее.

Оценка эксперта: 4 балла.

79

Пример 2.

Каждое из чисел 2, 3, …, 7 умножают на каждое из чисел 13, 14, …, 21 и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Ответ: 1 и 4131. (См. критерии задачи 1.)

80