
2012_МА_часть_1_методические рекомендации
.pdf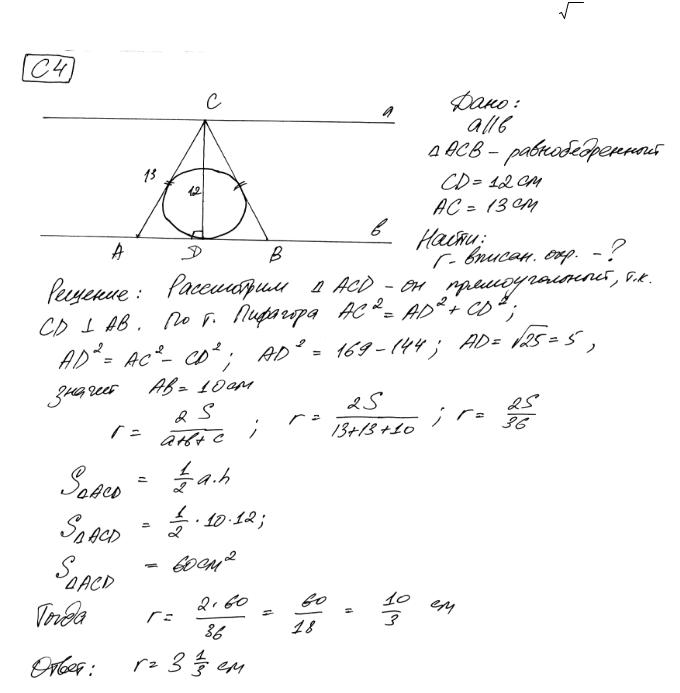
Пример 2.
Расстояние между параллельными прямыми равно 12. На одной из них лежит точка C , а на другой – точки A и B , причем треугольник ABC – равнобедренный и его боковая сторона равна 13. Найдите радиус
окружности, вписанной в треугольник ABC . Ответ: |
10 |
или |
39 −9 13 |
. |
|
3 |
2 |
||||
|
|
|
Комментарий. Это тот самый типичный случай, о котором говорилось во введении: «Есть верный рисунок одной конфигурации, есть правдоподобная цепочка вычислений, приводящая для этой конфигурации к верному ответу? Если есть, то значит, это, скорее всего, 2 балла, если только в вычислениях нет ошибок». Ясно, что здесь вычисления проведены достаточно аккуратно. Случай второй конфигурации вообще не рассмотрен.
Оценка эксперта: 2 балла.
51

Пример 3.
Расстояние между параллельными прямыми равно 12. На одной из них лежит точка C , а на другой – точки A и B , причем треугольник ABC – равнобедренный и его боковая сторона равна 13. Найдите радиус
окружности, вписанной в треугольник ABC . Ответ: |
10 |
или |
39 −9 13 |
. |
|
3 |
2 |
||||
|
|
|
Комментарий. Тоже весьма стандартное положение. Почти то же самое, что и в предыдущем примере 2, но при вычислении радиуса вписанной окружности есть ошибка, которая, к сожалению, отмечена экспертом прямо в проверяемой работе. Площадь делится на периметр, а не на полупериметр. Поэтому ответ – в два раз меньше. Случай второй конфигурации вообще не рассмотрен.
Оценка эксперта: 1 балл.
52
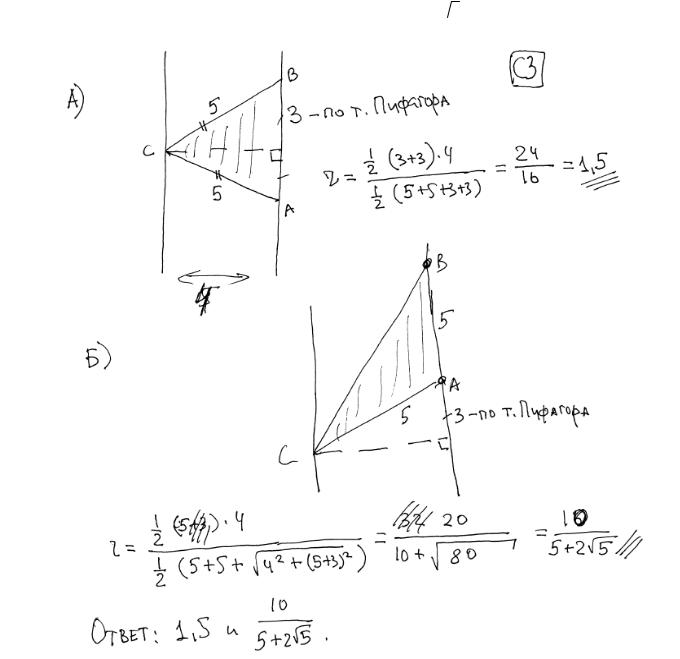
Пример 4.
Расстояние между параллельными прямыми равно 4. На одной из них лежит точка C , а на другой – точки A и B , причем треугольник ABC – равнобедренный и его боковая сторона равна 5. Найдите радиус окружности, вписанной в треугольник ABC . Ответ: 1,5 или 10 − 4 5 .
5 .
Комментарий. Рисунки неаккуратные, есть зачеркивания и исправления, общих формул для площади, полупериметра, радиуса нет, номер задачи указан неверно, иррациональность из знаменателя не убрана и т.д.
Но при спокойном взгляде на решение становится ясно, что снижать оценку тут не за что: это полное решение с верным ответом и с достаточными для такой планиметрической задачи обоснованиями.
Оценка эксперта: 3 балла.
53
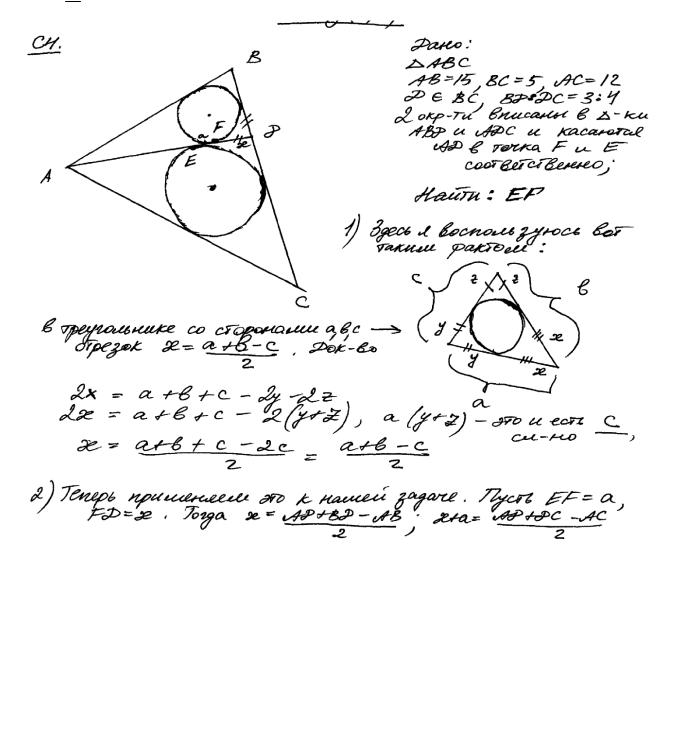
Пример 5.
В треугольнике ABC AB =15 , BC = 5 , AC =12 . Точка D лежит на прямой BC так, что BD : DC =3: 4 . Окружности, вписанные в каждый из треугольников ADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF .
Ответ: 137 или 4.
Комментарий. Прямо по критерию «Рассмотрена хотя бы одна возможная конфигурация, для которой получено правильное значение искомой величины». Автор «пропустил» второй случай, когда точка D лежит вне отрезка BC : ясно, что тем же способом он разбирается аналогично.
Оценка эксперта: 2 балла.
54

Пример 6.
В треугольнике ABC AB =15 , BC = 7 , AC = 9 . Точка D лежит на прямой BC так, что BD : DC = 2 : 3. Окружности, вписанные в каждый из треугольников ADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF . Ответ: 6,5 или 3,7.
Комментарий.
Красивое, лаконичное и верное решение, хотя окружности лучше бы рисовать и покруглее.
Оценка эксперта: 3 балла.
55
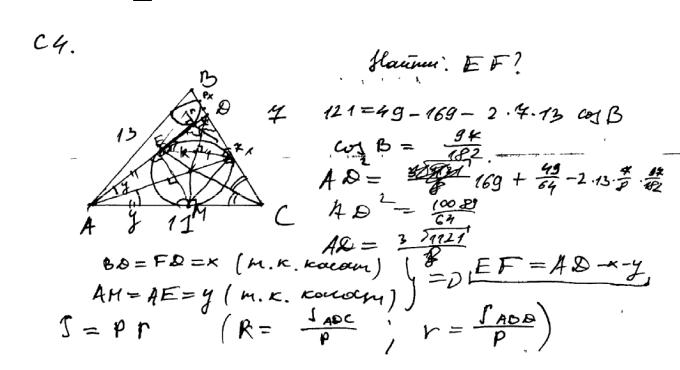
Пример 7.
В треугольнике ABC AB =13 , BC = 7 , AC =11 . Точка D лежит на прямой BC так, что BD : DC =1: 7 . Окружности, вписанные в каждый из треугольниковADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF .
Ответ: 4,5 или 298 .
Комментарий. Какие-то умения по решению планиметрических задач автор явно демонстрирует, но их, очевидно, не хватает для выставления положительного балла.
Оценка эксперта: 0 баллов.
56
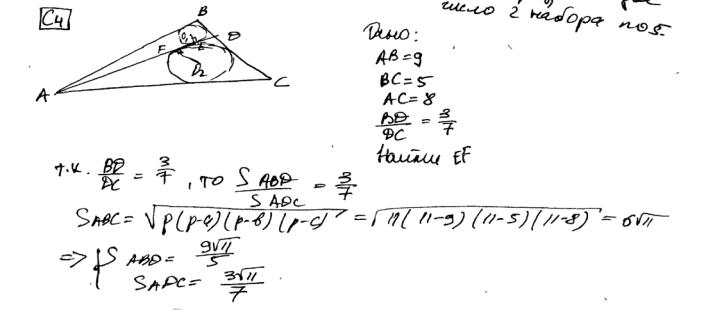
Пример 8.
В треугольнике ABC AB = 9 , BC = 5 , AC =8 . Точка D лежит на прямой BC так, что BD : DC = 3: 7 . Окружности, вписанные в каждый из треугольниковADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF .
Ответ: 1,5 или 3.
Комментарий. Случай, аналогичный Примеру 7.
Оценка эксперта: 0 баллов.
57

Пример 9. |
AC =12 . Точка D лежит на прямой BC |
В треугольнике ABC AB =14 , BC =10 , |
|
так, что BD : DC =3: 7 . Окружности, |
вписанные в каждый из треугольников |
ADC и ADB , касаются стороны AD в точках E и F . Найдите длину отрезка EF . Ответ: 3 или 6.
Комментарий. План намечен довольно разумный и, наверное, реализуемый. Но, проверим, правда ли, что AD =13? Если это так, то
cos B = 9 +196 −169 |
=100 +196 −144 |
9 + 27 |
=152 . |
2 3 14 |
2 10 14 |
3 |
10 |
Неверно! Приведенные автором вычисления можно трактовать и как сознательную попытку «обмануть» проверяющего, и как честное обманывание самого себя, связанное с ошибками в вычислениях. Если судить «в пользу ученика», то – 1 балл.
Оценка эксперта: 1 балл.
58
§5. Задания с развернутым ответом повышенного уровня сложности С5. Критерии проверки и оценки решений.
В этом параграфе представлены решения четырех задач: из ЕГЭ–2011 (задача 1), из диагностической работы, декабрь 2011 (задача 2), из ЕГЭ– 2010 (задача 3) и из диагностической работы, декабрь 2010 (задание 4). Их объединяет два момента: это задачи с параметром и это задачи, стоящие на месте С5.
Различие состоит в том, что задачи 1 и 3 явно носят функциональный оттенок, то есть связаны с исследованием поведения некоторой функции y = f (x, a) с параметром a , а задачи 2 и 4 связаны с системой уравнений. Как
это обычно бывает, задачи с параметром допускают либо чисто алгебраический способ решения, либо допускают способ решения, основанный на построении и исследовании простейшей геометрической модели.
Для задач 1–4 геометрический метод решения быстрее и точнее ведет к цели, а алгебраический либо технически сложнее, либо вообще вряд ли реализуем.
Задача 1.
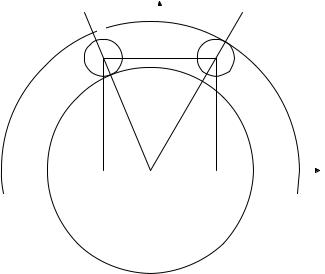
Найдите все положительные значения a , при каждом из которых система
( |
|
x |
|
−6)2 +(y −12)2 = 4, |
||||||
|
|
|||||||||
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
+ y |
= a |
||||||||
|
|
|
||||||||
(x +1) |
|
|
|
|||||||
имеет единственное решение. |
|
|
|
|
|
|
|
|
|||||||||||
Решение. |
|
|
|
|
|
|
|
y |
|
|
|
|
|||||||
Если |
|
|
x ≥0 , |
|
|
то |
уравнение |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
( |
|
x |
|
−6) |
2 |
+(y −12) |
2 |
= 4 |
задаёт |
|
B |
2 |
|
|
|
B1 |
|
||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
C2 |
|
|
12 |
C1 |
|
|||||||||
окружность ω1 |
|
с центром в точке |
|
|
|
|
|||||||||||||
|
ω2 |
A2 |
|
A1 |
ω1 |
|
|||||||||||||
C1 (6; 12) |
радиуса 2, а если x <0 , то |
|
|
|
|
|
|
ω |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
оно задаёт окружность ω2 |
с центром |
|
|
|
|
|
|
|
|
||||||||||
в точке |
|
C2 (−6; 12) того же радиуса |
|
|
|
C |
|
|
|
|
|||||||||
(см. рис.). |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
–6 |
–1 |
|
0 |
6 |
x |
||||||||||
При положительных значениях |
|
|
|
|
|
|
|
|
|||||||||||
параметра a уравнение |
|
|
|
|
|
|
|
|
|
||||||||||
(x +1)2 + y2 = a2 |
задаёт окружность ω |
|
|
|
|
|
|
ω |
|
||||||||||
с центром в точке C (−1; 0) радиуса |
|
|
|
|
|
|
|
|
|||||||||||
a . Поэтому задача состоит в том, |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||
чтобы найти все значения параметра a , при каждом из которых окружность ω имеет единственную общую точку с объединением окружностей ω1 и ω2 .
59

Из точки C проведём луч CC1 и обозначим A1 и B1 точки его пересечения с окружностью ω1 , где A1 лежит между C и C1 . Так как
|
CC = (6 +1)2 +122 |
= 193 , то CA = |
193 −2, CB = 193 + 2 . |
||
|
1 |
|
1 |
1 |
|
|
При a < CA1 или a >CB1 окружности ω и ω1 не пересекаются. |
||||
|
При CA1 < a <CB1 окружности ω и ω1 имеют две общие точки. |
||||
|
При a = CA1 или a =CB1 окружности ω и ω1 касаются. |
||||
|
Из точки C проведём луч CC2 и обозначим A2 и B2 точки его |
||||
пересечения с |
окружностью |
ω2 , где A2 |
лежит между C и C2 . Так как |
||
CC = |
(−6 +1)2 |
+122 =13, то CA =13 − 2 =11, CB =13 + 2 =15. |
|||
2 |
|
|
2 |
|
2 |
|
При a <CA2 или a >CB2 |
окружности ω и ω2 не пересекаются. |
|||
|
При CA2 < a < CB2 окружности ω и ω2 |
имеют две общие точки. |
|||
|
При a =CA2 или a =CB2 |
окружности ω и ω2 касаются. |
|||
Исходная система имеет единственное решение тогда и только тогда, когда окружность ω касается ровно одной из двух окружностей ω1 и ω2 и не
пересекается с другой. Так как CA2 <CA1 <CB2 < CB1 , то условию задачи удовлетворяют только числа a =11 и a = 193 +2.
Ответ: 11; 193 + 2 .
Содержание критерия |
Баллы |
Обоснованно получен верный ответ |
4 |
С помощью верного рассуждения получены оба верных значения |
3 |
параметра, но |
|
– или в ответ включены также и одно-два неверных значения; |
|
– или решение недостаточно обосновано |
|
С помощью верного рассуждения получено хотя бы одно верное |
2 |
значение параметра |
|
Задача сведена к исследованию: |
1 |
– или взаимного расположения трёх окружностей; |
|
– или двух квадратных уравнений с параметром |
|
Решение не соответствует ни одному из критериев, перечисленных |
0 |
выше |
|
Максимальный балл |
4 |
60
