
2012_МА_часть_1_методические рекомендации
.pdf
Задача 2.
Найдите все значения a , при каждом из которых наименьшее значение функции f (x)= 4ax + x2 −6x +5 больше, чем – 24.
Решение.
1. Функция f (x) имеет вид:
а) при x2 −6x +5 = (x −1)(x −5)≥ 0 f (x)= 4ax + (x2 −6x +5)= x2 + 2(2a −3)x +5,
а ее график состоит из двух частей параболы с ветвями, направленными
вверх, и осью симметрии x = 3 − 2a ;
б) при (x −1)(x −5)≤ 0 1 ≤ x ≤ 5 f (x)= 4ax −(x2 −6x +5)= −x2 + 2(2a +3)x −5 ,
а ее график представляет собой часть параболы с ветвями, направленными вниз.
2. Если 3 − 2a принадлежит отрезку [1; 5], то наименьшее значение функция может принимать только в конечных точках x =1 и x = 5 . Если 3 − 2a [1; 5] – то
еще и в точке x = 3 − 2a . |
|
|
|
|
f (x) больше – 24 тогда и только тогда, |
||||||||||||||
3. Наименьшее значение функция |
|||||||||||||||||||
когда |
|
|
|
|
|
|
|
|
3 |
−2a [1; 5], |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
3 |
− 2a [1; 5], |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
f (1)> −24, |
|
|
|
|
|||||
|
|
|
|
|
либо |
|
f (1)> −24, |
|
|
|
|
||||||||
|
|
|
|
|
|
либо |
f (5)> −24, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
f (5)> −24, |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решим первую систему: |
|
|
|
|
f (3 −2a)> −24. |
|
|
||||||||||||
≤ 3 − 2a ≤ 5, |
−1 ≤ a ≤1, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
f (1)> −24, |
|
4a > −24, −1 ≤ a ≤1 . |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
f (5)> −24, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
20a > −24, |
|
|
|
|
|
|
||||
Решим вторую систему: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
−1,2 < a < −1 |
|
3 − 29 |
|
|
|
3 + |
|
29 |
|
|
|||||||
|
|
|
a >1, |
|
|
< a < −1 или |
1 < a < |
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
2 |
|
|
||||||||||||||
|
|
|
|
2a |
−3 |
|
< 29, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: |
3 − 29 |
< a < |
3 + |
29 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Содержание критерия |
|
|
|
|
|
Баллы |
||||||
Обоснованно получен верный ответ |
|
|
|
|
|
|
|
4 |
|||||||||||
С помощью верного рассуждения получены все верные значения |
3 |
||||||||||||||||||
параметра, но решение недостаточно обосновано |
|
|
|
|
|
||||||||||||||
С помощью верного рассуждения получен промежуток, содержащий |
2 |
||||||||||||||||||
верный ответ, либо содержащийся в верном промежутке |
|
|
|
||||||||||||||||
Задача сведена к исследованию взаимного расположения частей |
1 |
||||||||||||||||||
двух парабол |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение не соответствует ни одному из критериев, перечисленных |
0 |
||||||||||||||||||
выше |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Максимальный балл |
4 |
||||
61
Задача 3. |
значения a , при каждом из которых функция |
Найдите все |
|
f (x)=x2 −2 | x −a2 | − 8x имеет более двух точек экстремума. |
|
Решение. |
|
1. Функция f |
имеет вид: |
а) при x ≥ a2 : |
f (x)=x2 −10x + 2a2 , поэтому ее график есть часть параболы |
с ветвями, направленными вверх, и осью симметрии x =5 ; |
|
б) при x ≤ a2 : |
f (x)=x2 −6x −2a2 , поэтому ее график есть часть параболы с |
ветвями, направленными вверх, и осью симметрии x =3 .
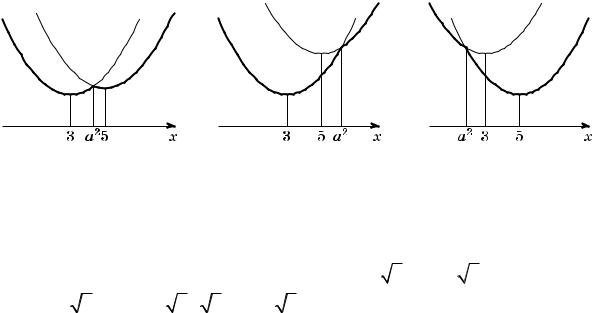
Все возможные виды графика функции f (x) показаны на рисунках:
Рис. 1 |
Рис. 2 |
Рис. 3 |
2. Графики обеих |
квадратичных функций |
проходят через точку |
(a2; f (a2 )) . |
|
|
3. Функция y = f (x) |
имеет более двух точек экстремума, а именно – три, |
|||||
в единственном случае (рис. 1): 3<a2 <5 |
3 < | a |< |
5 . |
|
|||
Ответ: − 5 < a < − |
3; |
3 < a < 5 . |
|
|
|
|
|
|
|||||
Критерии оценивания выполнения задания С5, №3 |
Баллы |
|||||
|
|
|
||||
Обоснованно получен правильный ответ |
|
4 |
||||
|
|
|||||
Получен верный ответ. Решение в целом верное, но либо |
3 |
|||||
имеет пробелы (например, не описаны необходимые свойства |
||||||
функции), либо содержит вычислительные ошибки |
|
|
||||
Верно рассмотрены все случаи раскрытия модулей. При |
|
|||||
составлении или решений условий на параметр допущены ошибки, |
2 |
|||||
в результате которых в ответе либо приобретены посторонние |
||||||
|
||||||
значения, либо часть верных значений потеряна |
|
|
||||
|
|
|||||
Хотя бы в одном из случаев раскрытия модуля составлено |
1 |
|||||
верное условие на параметр либо построен верный эскиз графика |
||||||
функции в целом |
|
|
|
|
|
|
Решение не |
соответствует ни |
одному из |
критериев, |
0 |
||
перечисленных выше |
|
|
|
|||
|
|
|
|
|||
62
Подчеркнем, что приведенный критерий на 3 балла формально содержит внутреннее противоречие: «Получен верный ответ…» не сочетается с «…либо содержит вычислительные ошибки». Более точно, имелось в виду следующее:
«Решение в целом верное, но:
либо получен верный ответ, а обоснования имеют пробелы (например, не описаны необходимые свойства функции); либо в обосновании пробелов нет, но ответ неверен из-за вычислительных ошибок».
Задача 4.
Найдите все значения параметра a , при каждом из которых система
y 2 + xy −4x −9 y + 20 = 0,y = ax +1,
x > 2
имеет единственное решение.
Решение. Преобразуем исходную систему
( y −4)x + yy = ax +1,x > 2
2 −9 y + 20 = 0, |
( y −4)x + |
( y −4)( y −5) =0, |
|
( y −4)(x + y −5) =0, |
|
|
|
+1, |
|
|
|
|
y = ax |
|
y = ax +1, |
||
|
|
|
|
|
|
|
x > 2 |
|
|
|
x > 2 |
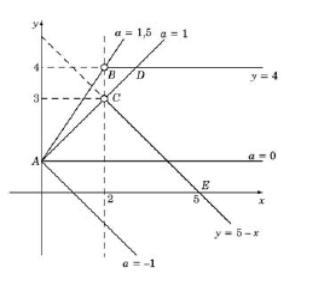
Уравнение ( y −4)(x + y −5) = 0 |
задает пару пересекающихся прямых y = 4 и |
||
y =5 − x . Система |
x > 2, |
|
задает |
|
|
||
|
( y −4)(x + y −5) = 0 |
|
|
части этих прямых, расположенные правее прямой x = 2 , т.е. лучи BD и CE (без точек B и C ), см. рис. Уравнение y = ax +1 задает
прямую m с угловым коэффициентом a , проходящую через точку A(0;1) . Следует
найти все значения a , при каждом из которых прямая m имеет единственную общую точку с объединением лучей BD и CE .
а) Прямая AB задается |
уравнением |
y =1,5x +1. Поэтому при a ≥1,5 |
прямая m не |
пересечет ни луч BD , ни луч CE .
б) Прямая AC задается уравнением y = x +1. Поэтому при 1 ≤ a <1,5 прямая
m пересечет луч BD , но не пересечет луч CE .
в) При 0 < a <1 прямая m пересечет и луч BD , и луч CE .
63
г) Наконец, при −1 < a ≤ 0 прямая m пересечет только луч CE , а при a ≤ −1 она не пересечет ни луч BD , ни луч CE .
Схема другого решения.
- В уравнение y 2 + xy −4x −9 y + 20 = 0 подставить y = ax +1;
-Привести подобные, найти дискриминант и получить (ax −3)(x(a +1) −4) = 0 ;
-Рассмотреть все случаи расположения корней последнего уравнения
относительно 2 и отобрать нужные.
Ответ. −1 < a ≤ 0, 1 ≤ a <1,5.
Критерии оценивания выполнения задания С5, №4 |
Баллы |
Обоснованно получен правильный ответ |
4 |
Решение в целом верное. Обоснованно найдены оба промежутка |
|
значений параметра из ответа к задаче, при этом возможны |
3 |
неточности с (не)включением концов и(или) вычислительная |
|
погрешность |
|
Обоснованно найден хотя бы один промежуток значений параметра |
|
из ответа к задаче, при этом возможны неточности с (не)включением |
2 |
концов и(или) вычислительная погрешность |
|
Решение содержит: |
|
- или верное описание расположения двух лучей и прямой из условия |
|
задачи; |
1 |
- или верное получение квадратного уравнения с параметром а |
|
относительно одной из переменных |
|
Решение не соответствует ни одному из критериев, перечисленных |
0 |
выше |
|
Отметим еще одну особенность рассматриваемых заданий с параметром. Практика проверки реальных работ учеников показала, что правильно построенная и грамотно изображенная геометрическая модель задачи зачастую не только необходима, но и в определенном смысле достаточна для получения высокого балла при оценивании решения.
Например, если в предложенном выше способе решения задачи 4 оставить преобразования системы, рисунок в его имеющемся виде и сопроводить этот рисунок лишь кратким перечнем типа « a >1,5 - 0 решений,
1 ≤ a <1,5 - одно решение, …., a ≤ −1 - 0 решений», то меньше 3 баллов поставить будет невозможно.
64

Примеры оценивания заданий С5.
Пример 1.
Найдите все положительные значения a , при каждом из которых система
(x −6)2 +(y −12)2 = 4,
(x +1)2 + y2 = a2
имеет единственное решение.
Ответ: 11; 193 + 2 . (См. критерии задачи 1.)
Комментарий. Подход, как говорят, «в принципе» верен. Одно нужное значение параметра найдено верно и обоснованно (хорошо, что в ответе есть исправление). Так что по критериям менее 2 баллов - не поставить. Нельзя поставить и более 2 баллов, так как не «…получены оба верных значения параметра…»
Оценка эксперта: 2 балла.
65

Пример 2.
Найдите все положительные значения a , при каждом из которых система
(x −6)2 +(y −12)2 = 4,
(x +1)2 + y2 = a2
имеет единственное решение.
Ответ: 11; 193 + 2 . (См. критерии задачи 1.)
Комментарий. Имеется классическая ученическая ошибка с «отбрасыванием» модуля. В итоге, хотя одно значение параметра, при котором происходит касание, и найдено верно, но это – именно то значение, которое не является верным из-за пропущенной второй окружности с центром (-6; 12).
Оценка эксперта: 0 баллов.
66
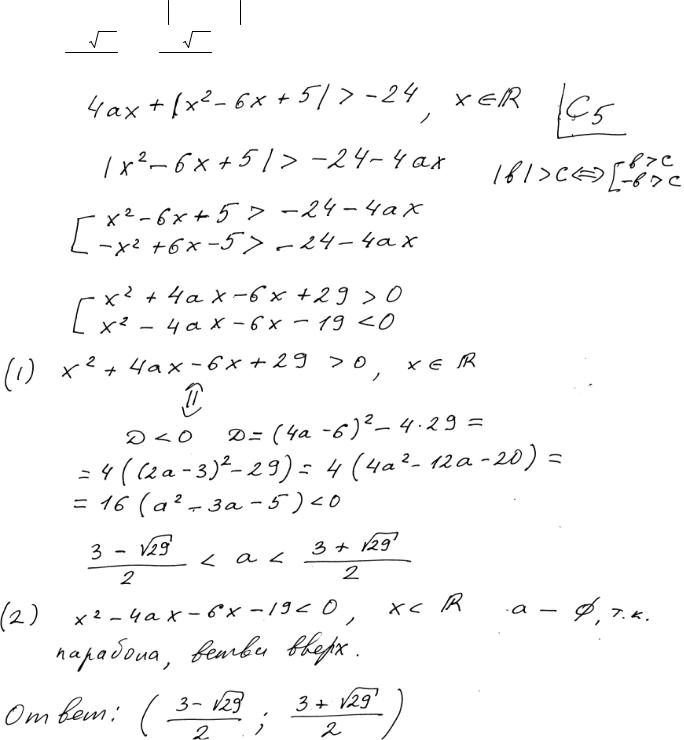
Пример 3.
Найдите все значения a , при каждом из которых наименьшее значение функции f (x)= 4ax + x2 −6x +5 больше, чем – 24.
Ответ: 3 −2 29 < a < 3 +2 29 . (См. критерии задачи 2.)
Комментарий. Получен верный ответ, но получен он не обоснованно! На
формальном языке, |
утверждение x ( A или B) заменено утверждением |
( x A) или ( x B) , что |
является обычной, но весьма грубой логической |
ошибкой. Конкретнее, при решении неравенства (1) (или (2)) ошибка состоит в том, что рассматриваются x R , а нужно рассматривать x вне отрезка [1;5] (или x в отрезке [1;5]). Значит, задача не «…сведена к исследованию взаимного расположения частей двух парабол…»
Оценка эксперта: 0 баллов.
67

Пример 4.
Найдите все значения a , при каждом из которых наименьшее значение функции f (x)= 4ax + x2 −6x +5 больше, чем – 24.
Ответ: 3 −2 29 < a < 3 +2 29 . (См. критерии задачи 2.)
Комментарий. Имеется арифметическая ошибка при делении на -4. Без нее ответ совпадал бы с верным ответом. Однако для обоснованного получения ответа не достаточно одного неравенства y верш > −24 . Кроме того,
явно не хватает указания тех промежутков, где автор «раскрывает модуль» с плюсом или с минусом. С некоторой натяжкой, но задача «…сведена к исследованию взаимного расположения частей двух парабол…»
Оценка эксперта: 1 балл.
68

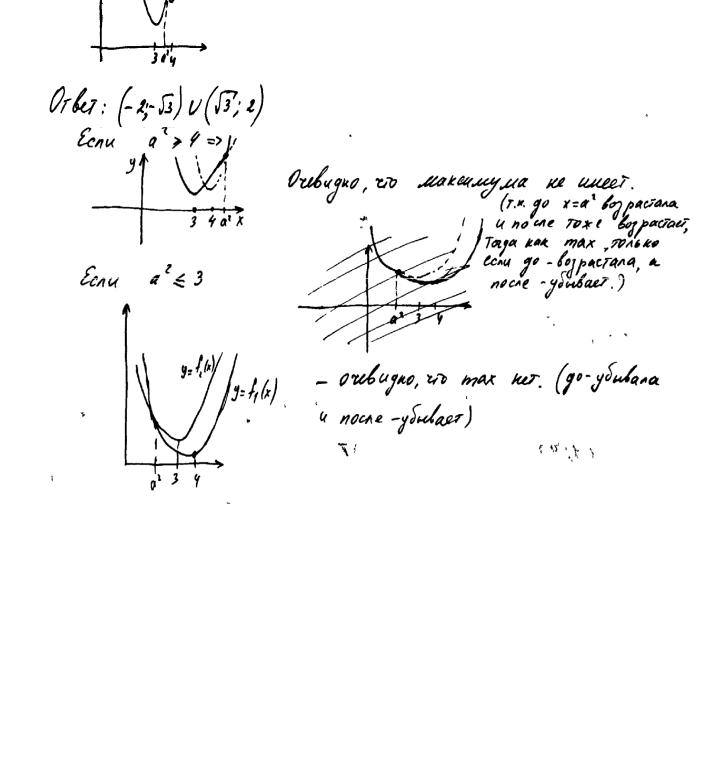
Пример 5. Найдите все значения a , при каждом из которых функция f (x)=x2 −| x −a2 | −9x имеет более двух точек экстремума.
Ответ: −  5 < a < −
5 < a < − 2 ;
2 ;  2 < a <
2 < a <  5 . (См. критерии задачи 3.)
5 . (См. критерии задачи 3.)
Комментарий.
Ответ верен с точностью до странности 4 и описки − 2 , вместо
−2 = − 4 . В оригинале текста самое загадочное – это индексы у абсцисс вершин парабол. Фотоувеличение показывает, что это «extr» - экстремум. В остальном, - довольно ясно и прямо по критериям: «…Решение в целом верное, но либо имеет пробелы (например, не описаны необходимые свойства функции),…»
Оценка эксперта: 3 балла.
69
Пример 6. Найдите все значения a , при каждом из которых функция f (x)=x2 −| x −a2 | −7x имеет более двух точек экстремума.
Ответ: −  5 < a < −
5 < a < − 2 ;
2 ;  2 < a <
2 < a <  5 . (См. критерии задачи 3.)
5 . (См. критерии задачи 3.)
Комментарий.
Модули раскрыты верно, имеются верные эскизы графиков во всех трех случаях и указаны необходимые свойства функции, ответ верен.
Оценка эксперта: 4 балла.
70
