Вопрос 11

Вопрос 11. Умножение многозначных чисел. Теоретический материал, рассматриваемый в данной теме.

В этой теме с помощью алгоритмов вводятся следующие вычислительные приемы:

1. Умножение на однозначное число.

2. Умножение на разрядные числа.

3. Умножение на двузначные и трехзначные числа.

На каждом из этих этапов изучаются сначала приемы умножения, затем деления. Возможны другие подходы в изучении данной темы.

На подготовительном этапе ведется повторение, обобщение и систематизация изученного материала. На этапе ознакомления сначала рассматриваются устные вычислительные приемы умножения разрядного числа на однозначное вида: 60003; 4002; 4сот. 2= 8 сот.=800

Теоретическая основа - конкретный смысл умножения.

Затем учащиеся подводятся к необходимости введения письменного приема умножения. С этой целью вводится прием умножения на однозначное число с переходом через десяток или сотню.

На основе алгоритма умножения из курса математики составляется и вводится алгоритм умножения в начальной школе. Однако письменное умножение начинаем с единиц низшего разряда, устное с единиц высшего разряда.

Рассуждения учащихся могут быть следующими: «записываю множители в столбик, один под другим. Проведем черту, слева ставим знак умножения. Второй множитель пишу под единицами.

1327

2

Начинаю умножение с единиц низшего разряда 7 единиц умножаю на 2 = 14 единиц, это 1 десяток 4 единицы, записываю 4 единицы под единицами, а 1 десяток запоминаю, чтобы потом прибавить к десяткам”.

Алгоритм объяснения можно записать в следующей последовательности:

Умножаю единицы:

Умножаю десятки:

Умножаю сотни:

Читаю ответ:

Сначала дается подробное объяснение, затем краткое. Когда алгоритм усвоен, название единиц каждого разряда можно опустить.

Необходимо научить детей:

1. правильно записывать множители;

2. познакомить со знаком умножения;

3. при умножении называть каждый разряд;

4. проговаривать промежуточные результаты

Усложнение приемов проходит в следующем порядке:

1. увеличивается число разрядов первого множителя;

3253; 62855 и т.д.;

2. Первый множитель содержит нули в середине или на конце, необходимо знание разрядного состава числа;

7056; 60078; 7060005 ….;

3. Различные сочетания этих случаев.

Например: 72500

8

Объяснение: подписываем второй множитель под первой цифрой первого множителя, отличной от нуля. 725 сот.  8=4350 сот. Или 435000.

Выполняют умножение, не обращая внимания на нули, записанные в конце 1 множителя и к полученному произведению приписывают столько нулей, сколько их в конце первого множителя. От подробного объяснения решения переходят к краткому, когда опускается название разрядных единиц и выполняемых преобразований.

Затем вводятся приемы умножения однозначного числа на многозначные:

86734 – теоретическая основа – переместительное свойство умножения.

Умножение на разрядные числа.

На подготовительном этапе рассматривается следующий теоретический материал:

1. умножение на однозначное число;

2. таблицы умножения и сложения;

3. умножение на 10, 100, 1000.

4. замена разрядных чисел произведением однозначного числа и 10, 100, 1000 (600=6100)

5. свойство умножения числа на произведение (сочетательный закон умножения):

1. 8 (42)=88=64

2. 8 (42)=(84) 2=64

Сочетательный закон умножения читается так: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего числа. Формулировка закона может быть другая: два или несколько множителей в произведении можно заменить их произведением, от этого значение арифметического выражения не изменится.

(ab) c = a (bc)

Свойство является теоретической основой для введения приемов.

На этапе ознакомления первыми вводится устные случаи вида:

1630=16 (310)=(163) 10=480

70060=700 (610)=(7006) 10=42000

Рассуждения учащихся: чтобы 7 сотен умножить на 60, надо 7 сотен умножить на 6, а затем полученное число умножить на 10, будет 42 сотни или 42000 единицы.

Теоретическая основа – сочетательный закон умножения или умножение числа на произведение.

Затем вводятся письменные приемы.

Например:

3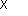75

40

Второй множитель записываем так, чтобы нули были справа от единиц первого множителя. Число 375 умножаем на 4 и полученный результат умножаем на 10. В произведении записываем столько нулей, сколько их было во втором множителе.

Следующими рассматривается случай умножения, когда оба множителя оканчиваются нулями.

7200

60

Объяснение: 72 сотни умножаем на 6, получаем 432 сотни или 43200 и доумножаем на 10.

Вопросы вида:

• Сколько нулей в 1 множителе?

- Сколько нулей во 2 множителе?

• Сколько нулей в произведении?

Вывод: чтобы умножить 2 числа с нулями на конце, надо перемножить их, не обращая внимания на нули, а затем к полученному произведению приписать столько нулей, сколько их записано в конце обоих множителей вместе.

Теоретическая основа – свойство умножения числа на произведение.

Умножение на двузначное и трехзначное число.

Сначала на этой основе вводится случай вида:

3013=30 (10+3)=300+90=390

Письменные приемы умножения на двузначные числа вводится на примере вида: 7836

Показывается запись в строчку:

7836=78 (30+6)=7830+786=2808

Делается вывод, чтобы устно вычислить результат сложно. Произведения 7830 и 786 записываются в столбики, результаты вычисления называют неполными произведениями; сложив их, получаем произведение чисел 78 и 36.

Затем два столбика объединяются в один. Возможен и другой вариант введения умножения в столбик.

- Сравните 2 примера.

78. 78

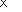
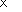6. 36

468. 468

Как продолжить умножение во втором примере?

Вводится алгоритм умножения.

1. Умножаю на единицы (78 умножаем на 6), получим 1 неполное произведение.

2.Умножаю на десятки (78 умножаем на 30), получим 2 неполное произведение.

3.Читаю ответ. Сложив неполные произведения, получаем ответ.

Нуль в конце второго неполного произведения можно не писать, так как сложив число единиц первого неполного произведения с нулем получим число единиц первого неполного произведения. При умножении на число десятков второе неполное произведение начнем подписывать под десятками первого неполного произведения.

Теоретическая основа – свойства умножения числа на сумму.

Умножение на трёхзначное число вводится на основе умножения на двузначное. Можно использовать такой прием: к числам 78 и 36 добавим цифру, обозначающую число сотен, например 4 и 5, получим пример 478536.

Как получить третье неполное произведение?

483 умножаем на 3, на число сотен и результат умножением на 100, 3-е неполное произведение подписываем под сотнями.

Затем включаются частные случаи умножения: умножение чисел, в записи которых на конце или в середине есть нули. Алгоритм умножения остается тот же, хотя имеются некоторые особенности.

Например:

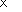1. 560

74

Чтобы умножить 560 на 74, надо 56 дес. умножить на 74, получим десятки, их заменим единицами, приписав справа нуль.

7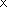48

306

В этом случае от умножения на единицы сразу переходим к умножению на сотни. Умножаем 748 на 300, получаем 2244 сотни или 224400.

В сумме будут отсутствовать единицы какого-либо разряда, в данном примере отсутствуют десятки и от умножения на единицы переходим к умножению на сотни; второе неполное произведение подписываем под сотнями.

Т.о. последовательно, по степени сложности рассматриваются все случаи письменного умножения.

Умножение на двузначное и трехзначное числа.

Изучение действий разделено на два этапа:

1. умножение и деление на двузначное число (осваивается алгоритм, формируются все понятия);

2. умножение и деление на трехзначное число (перенос полученных понятий и умений на более сложный материал).

Анализ выполнения умножения показывает, что основные положения те же, что и при умножении на однозначное число: поразрядность выполнения умножения и использование в каждом разряде таблицы умножения.

Вместе с тем существуют особенности.

Например: 70  4=280 700  4=2800

Находят результат известными способами. Определяют сходство и различие этих равенств и разницу в разрядных единицах. Затем исследуют источник подмеченной закономерности, осознают основной путь выполнения действия - представление множителя не произведением любых чисел, а произведением однозначного числа на единицу с нулями. Отсюда вытекает необходимость знания о закономерности, связанной с умножением любого числа на разрядную единицу.

Выделим основные этапы в изучении умножения на двухзначное число: сочетательный закон умножения; умножение на единицу с нулями на основе использования сочетательного закона умножения; умножение на круглые десятки на основе использования того же закона, распределительный закон умножения относительно сложения; умножение на двузначное число со всеми значащими цифрами. Необходимо установление логических связей между отдельными этапами и между новым материалом и изученным.

Алгоритм умножения на однозначное число - основа овладения алгоритмом умножения на двузначное и трехзначное числа.

2