
- •Министерство образования российской федерации
- •Содержание
- •Предисловие
- •1 Лабораторная работа. Измерение физических величин и классификация их погрешностей
- •1.1 Прямые измерения основных физических величин
- •1Б) Гладкий микрометр мк:
- •1 Скоба, 2 – пятка, 3 – микрометрический винт, 4 – стопор, 5 – барабан, 6 – трещетка. Рисунок 1.1
- •1.2 Погрешность измерений
- •1.2.3 Приборная погрешность
- •1.3 Запись результатов наблюдений
- •1.4 Построение графиков и таблиц
- •1.5 Погрешность косвенных измерений
- •1.6 Определение плотности твердых тел правильной геометрической формы
- •1.8 Контрольные вопросы
- •2 Лабораторная работа. Исследование законов вращательного движения
- •2.1 Основные понятия и закономерности
- •А бРисунок 2.2
- •2.2 Теория метода и описание установки
- •2.3 Порядок выполнения работы
- •2.4 Контрольные вопросы
- •2.5 Техника безопасности
- •3 Лабораторная работа. Определение момента инерции различных тел методом крутильных колебаний
- •3.1 Основные понятия и закономерности
- •3.2 Теория метода и описание установки
- •3.3 Порядок выполнения работы
- •3.4 Контрольные вопросы
- •3.5 Техника безопасности
- •4 Лабораторная работа. Изучение соударения шаров
- •4.1 Основные понятия и закономерности
- •4.2 Методика работы и описание установки
- •4.3 Порядок выполнения работы
- •4.4 Контрольные вопросы
- •4.5 Техника безопасности
- •5 Лабораторная работа. Определение ускорения свободного падения при помощи маятника
- •5.1 Основные понятия и закономерности
- •5.2 Описание установки и теория метода
- •5.3 Порядок выполнения работы
- •6 Лабораторная работа. Определение отношения теплоемкостей газов по методу клемана и дезорма
- •6.1 Основные понятия и закономерности
- •7 Лабораторная работа. Определение коэффициента вязкости жидкости с помощью капиллярного вискозиметра и методом стокса
- •7.1.1 Теоретические сведения
- •7.1.2 Вискозиметр Оствальда
- •7.1.3 Порядок выполнения работы
- •7.2 Определение коэффициента вязкости жидкости методом
- •7.2.1 Основные понятия и закономерности
- •7.2.2 Краткая теория метода
- •7.2.3 Порядок выполнения работы
- •7.4 Техника безопасности
- •Приложение а
- •8 Лабораторная работа. Определение ёмкости конденсаторов Цель работы:
- •8.1 Основные понятия
- •8.2 Теория метода и схема установки
- •8.3 Порядок выполнения роботы
- •8.4 Контрольные вопросы
- •8.5 Техника безопасности
- •9.1 Основные понятия и законы
- •9.2 Порядок выполнения работы
- •9.3 Контрольные вопросы
- •9.4 Техника безопасности
- •10 Лабораторная работа измерение сопротивлений проводников методом мостиковой схемы
- •10.1 Основные понятия и закономерности
- •10.4 Контрольные вопросы
- •10.5 Техника безопасности
- •Сборник лабораторных работ по общему курсу физики
- •Часть I
- •173003, Великий Новгород, ул. Б. Санкт-Петербургская, 41.
4.4 Контрольные вопросы
Сформулировать и записать закон сохранения импульса.
Сформулировать и записать закон сохранения энергии в механике.
Вывести формулу скоростей шаров после упругого и неупругого ударов.
Вывести рабочие формулы для отношения масс шаров, скорости шаров перед и после удара, коэффициент восстановления шаров.
Каков физический смысл коэффициента восстановления шаров К ?
Вывести формулу для вычисления погрешностей.
4.5 Техника безопасности
1. Перед выполнением работы проверить прочность закрепления всех частей установки.
2. Не включать электрическую схему без проверки преподавателем или лаборантом.
5 Лабораторная работа. Определение ускорения свободного падения при помощи маятника
Цели работы:
определить ускорение свободного падения методом математического маятника,
сравнить результаты измерений с g0.
5.1 Основные понятия и закономерности
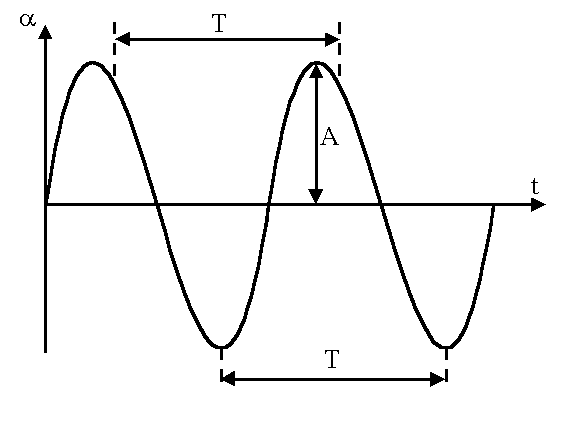
Гармоническим колебанием физической величины aназывается процесс изменения ее за времяtпо закону гармонической функции, например:
a = Asin(w t + jo),(5.1)
где А – амплитуда колебаний – максимальное значение колеблющейся величины,
w – циклическая частота колебания, величинаj = w t + joносит название фазы колебания,
jo– начальная фаза колебаний.
(jo =const). График такого колебания представлен на рисунке 5.1.
Периодом колебания называется промежуток времени, за который совершается одно полное колебание. При этом фаза колебания изменится на 2p,т.е.w (t + T) + jo = w t + jo + 2p,
откуда
w=
![]() .
(5.2)
.
(5.2)
 Рисунок
5.1
Рисунок
5.1
Величина w– круговая (циклическая) частота колебания, характеризует изменение фазы колебания за единицу времени.
Если начальная
фаза joравна
![]() ,
то уравнение гармонического колебания
записывается в виде:
,
то уравнение гармонического колебания
записывается в виде:
a = Acosw t.(5.3)
Примерами гармонических колебаний являются колебания физического и математического маятников.
Физическим маятникомназывается тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр тяжести, и способное совершать колебания относительно этой оси (рисунок 5.2).
 Рисунок
5.2
Рисунок
5.2
Математический маятник– это идеализированная система, состоящая из материальной точкиm, подвешенной на нерастяжимой невесомой нити и колеблющейся под действием силы тяжести. Хорошим приближением математического маятника является тяжелый шарик, подвешенный на тонкой длинной нити (диаметр шарика во много раз меньше длины нити, масса которой во много раз меньше массы шарика), второй конец которой закреплен неподвижно.
|
|
|
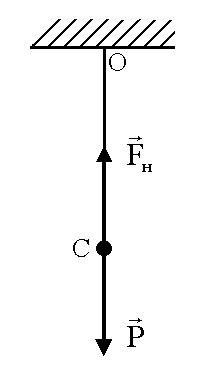
Если груз маятника неподвижен и находится
в положении равновесия (рисунок 5.3), на
него действуют сила тяжести
![]() =
=
![]() и сила натяжения
и сила натяжения![]() .
Эти силы уравновешивают друг друга
(направлены в противоположные стороны
.
Эти силы уравновешивают друг друга
(направлены в противоположные стороны
![]() = –
= –![]() ).
).
Докажем, что
маятник, отклоненный на малый угол aот положения равновесия, будет совершать
гармонические колебания. При отклонении
маятника на уголaот
положения равновесия силу тяжести![]() =
=
![]() можно разложить на две составляющие
(рисунок 5.4)
можно разложить на две составляющие
(рисунок 5.4)
ê![]() ê=
ê=![]() sinaиê
sinaиê![]() ê=
ê=![]() cosa.(5.4)
cosa.(5.4)
Сила
![]() уравновешивает силу натяжения
уравновешивает силу натяжения![]() СоставляющаяP1направлена вдоль касательной к траектории
движения маятника (движение по дуге
окружности АС к положению равновесия
с ускорением).
СоставляющаяP1направлена вдоль касательной к траектории
движения маятника (движение по дуге
окружности АС к положению равновесия
с ускорением).
В положении
равновесия (×) Сê![]() ê= 0, шарик по инерции
проходит это положение, а затем его
движение становится замедленным до
положения (×)B.
После максимального отклонения от
положения равновесия на уголaшарик будет двигаться обратно и такие
движения будут повторяться многократно
– шарик будет колебаться.
ê= 0, шарик по инерции
проходит это положение, а затем его
движение становится замедленным до
положения (×)B.
После максимального отклонения от
положения равновесия на уголaшарик будет двигаться обратно и такие
движения будут повторяться многократно
– шарик будет колебаться.
На основании закона динамики вращательного движения – момент силы lP1 равен произведению момента инерции шарикаIна угловое ускорениеe, имеем:
P1 l = Ie , (5.5)
где e = a11=d2a/dt2– угловое ускорение (вторая производная угла поворотаa по времени t),
I =ml2– момент инерции шарика, относительно оси, проходящей через точку 0 (момент инерции материальной точки),
l – длина маятника,
P1= –Psina= –mgsina– возвращающая сила (знак “–” обусловлен тем, чтоP1иa всегда противоположны).
sina » aприa£40– 60. Поэтому
P1 = – mga (5.6)
и уравнение (5.5) принимает вид:
– mgla = ml2a11,
ga + la11 = 0 (5.7)
или
a11
+
![]() a
= 0. (5.8)
a
= 0. (5.8)
Обозначив
![]() =w02,w0
=
=w02,w0
=
![]() ,
(5.9)
,
(5.9)
получим уравнение:
a11 + w0 2 = 0, (5.10)
где wо – циклическая частота колебаний маятника.
Уравнение (5.10) – уравнение гармонического осциллятора. Решение этого уравнения имеет вид уравнения гармонического колебания
a = aо cos (wо t + jо). (5.11)
Из соотношения (5.11) следует, что при малых углах отклонения математический маятник совершает гармонические колебания с циклической частотой wо и периодом колебанияТ.
Т=![]() =2p
=2p![]() . (5.12)
. (5.12)
Формулу (5.12) периода колебаний математического маятника можно использовать для определения ускорения свободного падения. Из формулы (5.12) следует, что период колебаний математического маятника не зависит от его массы.

 Рисунок
5.3
Рисунок
5.3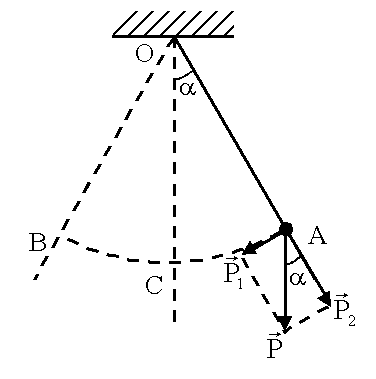 Рисунок
5.4
Рисунок
5.4