1 Понятие множества.

Понятие множества относ. к числу первоначальных понятий, которые не определяются через другие более простые. Мн-во еще наз. совокупность, собрание предметов. Предметы составляющие данное мн-во наз. элементами данного мн-ва.

Теорию конечных мн-в иногда наз. Комбинаторикой.

В матем. Допускаются к рассмотрению мн-ва не содержащие элементов-пустые мн-ва.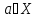 – а есть элемент мн-ва Х

О.Мн-во В наз. подмн-вом мн-ва А, если каждый элемент мн-ва В явл. Элементом мн-ва А.

Каждый отдельный элемент мн-ва А образует подмн-во, состоящее из этого элемента. Подмн-во мн-ва А наз. несобственным, если оно совпадает с мн-вом А. Если мн-во В есть подмн-вом А, значит В содержится в А

Подмн-во В мн-ва А наз. Собственным, если В не пусто и не совпадает с А.

2 Операции над мн-вами.

Пусть А и В – произв. Мн-ва.

Объедин. Двух мн-в А и В наз. Мн-вом С равному , состоящ. Из всех элементов принадлежащ. Хотя бы одному элементу А и В. Аналогично определяется определение любого – конечн. Или бесконечн. – числа мн-в: если А – произв. Мн-ва, тоі.Есть совокупность элементов, каждый із которых принадлежит одному из мн-в Аі.

Перечисление мн-в А и В наз. Мн-во С, сост. Из всех элементов, принадлежащих как к А, так и В. Перечислнием любого (конечного или бескон.) числа мн-в Аі наз. Мн-во элементов пренадлежащих каждому из мн-в Аі. Операции обьед. И пересеч. Мн-в по опред. Ассоциотивны и комутативны. ;

; ;.

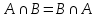Эти операции взаимно диструбутивны

О. Разностью мн-в А и В наз. Мн-во тех элементов из А, которые не содерж. в В.

3 Отображение мн-в. Понятие ф-и.

Пусть M и N – 2 произвольных мн-ва. О. На M определенная функц. f, принимающ. значение из N, если каждому элементу х𝜖М наз. Областью определения данной ф-и, а N – ее обл. значений. Для мн-в произвольной природы вместо термина функция часто польз. термином отображение, говоря об отображении одного мн-ва в другое.

Если а – элемент М, то соответств. ему элемент b=F(a) из N наз. образом a при отображении F. Совокупность всех тех элементов а из М, образом кот. явл. данный элемент b из N, наз. прообразом b и обознач. P^-1(b).

Пусть А - некот. мн-во из М совокупность.

всех элементов F(a), где (а𝜖А) наз. образом А(обозн. F(A)). В свою очередь для каждого мн-ва B из N опред-ся его поный прообраз р^-1(B), а именно F^-1(B) есть совокупность всех элементов из M, образы кот. принадлежат В.

О. Будем говорить, что F есть отображение мн-ва М на N, если F(M)=N , такое отображение мн-ва наз. сюрьекцией. Если для любых различных элементов х₁, х₂ из M их образы у₁=f(x₁), y₂=f(x₂) их образы также различны , то наз. f инъекцией. Отображение F:M⟶N, кот. одновр. явл. сюръекцией и инъекцией наз. взаимно однозначным соответствием между M и N.

5 Разбиение на классы. Отношение эквивалентности.

В самых различных вопросах втреч. разбиение тех или иных мн-в на попарно непересекающ. подмн-ва . Напр., плоскость можно разбить на прямые параллельные оси Х, жителей данного города можно разбить на группы по году рожд. и т. д.

Каждый раз, когда некот мн-во М представл. тем или иным способом как сумма попарно непересек. мн-в, мы говорим о различии мн-ва М на классы.

Пусть М – некот. мн-во и пусть некот. из пар (а,b) элементов из этого мн-ва явл. выделенными. Если (а,b) выдел. Пара, то мы говорим, эл-т а связан с b отношением 𝜑 и обознач. его символом а𝜑 b означает имеет ту же площадь, что и.

О. Отношением 𝜑 наз. отношение эквивалентности, если оно обладает след. Свойствами:

1. Рефлексивность а𝜑а для любого а𝜖М

2. Симетричность: если а𝜑b,то b𝜑a.

3. Транзитивность : если a𝜑b и b𝜑c,то a𝜑c.

Эти условия необходимы и достаточны для того, чтобы отношение 𝜑 (признак) позволяло разбить мн-во М на классы. Прямым (декарповым) произведением мн-в а₁, а₂, а₃ … а_n наз мн-во А₁×А₂×…А_n=.

Если А₁=А₂=…=А_n, то мн-во наз. прямой степенью мн-ва А и обозн_. Аⁿ.

Бинарным отношением между эл-ми мн-в А и В наз. подмн-вом R мн-ва А×В. Если А=В, то отношение R наз. бинарным отношением на А. Вместо (x,y)𝜖R часто пишут xRy.

Примером отношения может служить отношение тождества Е – (a,b)𝜖E в том и только том случае, когда a=b. Иначе говоря, это отношение вида (а;а).

Обл. определения бинарного отношения R наз. мн-во 𝜎_R={х⎸существует y такое, что (х;у)𝜖R}.

Обл. значений бинарн. отнош. R наз. мн-во 𝜌_R={x⎸ существует y такое, что (y,x) 𝜖R}.

Для бинарн. отношений определены обычным образом теоретико-множественные операции, обьедин. Перечисления и т. д.

Дополнением бинарн. отношения наз. R между элементами А и В наз. мн-во -R=(A×B)\R.

Обратным отношением для бинарн. отношения R наз. мн-во R^-1={(x,y)⎸(y,x)𝜖R}.

Образом мн-ва х относительно R наз. мн-во R(x)={y⎸существует x𝜖X такое, что (х;у)𝜖R}.

Произведением отношения R₁⊆A×B и R₂⊆B×C наз. отношением R_1* R₂={(х;у) существует Z такое, что (х;z)𝜖R (z;у)𝜖R₂}.