19 Основные правила дифференцирования. Производные сложной ф-ии. Некот положения производной

Т1: производная «+» («-») 2-ух диф. ф-ий равна «+» («-») в произв-ой этих ф-ий

Док-во: пусть , гдеи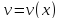диф. ф-ии. Поскольку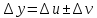, то=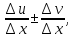тогда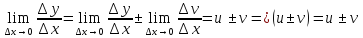. Т. доказана

Т2: произв-ая произведений 2-ух дифер-ых ф-ий равна произвед. 1-ой ф-ии на произ-ую 2-ой + произв-ая 2-ой на произв-ую 1-ой

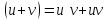
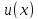Док-во: пусть , где=и- диф. ф-ии, т.к.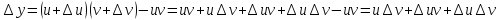, тогда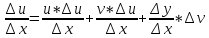. Согласно Т, тогда получим, что

Следствие: постоянный множит. можно выносить за знак производной

Т3: произв-ая частнuой 2-ух диф. ф-ий определ-ся формулой

Док-во: если , где– диф. ф-ии, причём

распишем: ;т.к.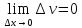. Т. доказана

Если у=f(х) и х= (у) – взаимообратные ф-ии и у`, тогда х_у=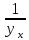действительно, т.к.т.е.откуда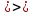х_у=

Производные сложной ф-ии.

Рассм. сложную ф-ию , где 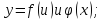в том случае- промежут. аргумент, х – независимая переменная

Т1 Если и- диф. ф-ия своих аргум., то произв-ясущ. и равна произведению произв-ой той ф-ии по промежут. аргум. На произв-ую промежут. аргум.; но независ. переменной.y`x=y`_u-u`_x

Док-во: в соотв. с усл. и по определ. Произв-ой 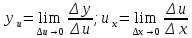т.к.тоy`_x=

Некот. положения произв-й

Т1 (Лагранжа). Если f(x) непрер. на отр. [a;b] и имеет конеч. произ-ую в интервале (a;b), то в этом интерв. найд-ся одна точка С, такая что

При исслед. ф-ий может появ. необход. нахождения предела дроби 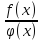, числит и знаменат кот при х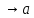сирем-ся к 0 или. Нахождение таких пределов наз раскрытием неопределён-ти соответств вида.

Основой явл права Лайпиталия выраж-й след Т: если ф-ия f(x) и диф-ием в окрестности, то х=а обращ-ся в 0. , то сущ предел отношений самих ф-ий равносильно пределу.

20 Признаки постоянства возр и убыв ф-ий

Т1 пусть ф-ия f(x) имеет конечную произв-ую в интервале (a;b). Чтобы f(x) была постоянной в (a;b) необход достаточно чтобы f`(x)=0 в этом интерв.

Док-во: если f(х)=const, то f`(x)=0. Докажем достаточность, т.е. если f`(x)=0 в интервале (a;b), то f(х)=const. Возьмём в интервале любые 2 значения х₁ и х (х₁ х) и применим ф-лу Лагранжаf(x)- f(x₁)=(х-х₁) f`(с). Точка С лежит между х и х<sub>1.</sub> Отсюда т.к. f`(x)=0, то f(x)- f(x₁)=0. f(x)-=f(x₁) при люб знач х(a;b); f(х)=const. ЧТД

Т2 пусть ф-ия f(x) непрер на (a;b) и меет на нём конечную произв-ую, тогда: 1) если f`(x)>0 на (a;b), то ф-ия возр на этом интерв. 2) если f`(x)<0, то ф0ия убыв.

Док-во 1: возьмём в интерв (a;b)люб знач х₁ и х₂ ( х₁ х₂) и применим Т Лагранжа, получим 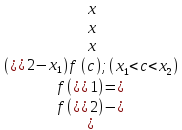, т.е. и по усл, то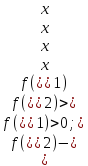- это и означавет, что ф0ия возр на(a;b). Для 2 аналогично

21 Max и min ф-ии необход и достат усл экстремума

ф-ия f(x) имеет в точке f(x₀) max, если в некот окрестности этой точке (при х х₀) выполн-ся нерав-во f(x) f(x₀). ф-ия f(x) имеет в точке x₀ min - f(x₀) если в некот окрестности этой точке (при х х₀) выполн-ся нерав-во f(x) f(x₀). Ф-ия f(x) в точке (x₁) имеет max f(x₁)=А₁М₁ а в точке х₂ min f(x₂)=А₂М₂.

Max и min ф-ии наз экстремумами ф-ий. Точка в кот имеет max или min наз точкой экстремума ф-ий. Необход усл экстремума даёт след Т: если ф-ия f(x) в точке х₀(a;b) имеет экстремум и в этой точке сущ конечная произв-ая, то она =0

Достаточное усл экстремума

Т1 если в точке х х₀ произв-я ф-ии у= f(x)=0 меняет знак при переходе через точку, то х₀ явл точкой экстремума, причём: 1) х₀ – точка max, если знак мен-ся с + на -; 2) х₀ – точка min, если знак мен-ся с – на +. Достаточно усл экстремума можно выразить с помощью 2-й прозв-й.

Т2 если в точке х х₀ произв-я ф-ии у= f(x)=0, а 2-я отличная от 0, то х₀ явл точкой экстремума, причём: 1) х₀ – точка min, если f``(x<sub>0</sub>)>0; 2) х<sub>0</sub> – точка max, если f``(x₀)<0