2) Если ф-ия f(X) интегрир-ая на наиб из отр [a;b], [a,c],[c,b], то она интегрируема на 2-х др отр, причём при любом положении точек a,b,c.

3) Если f(X) и ф-ии интегрир-ые на отр [a;b], то их сумма и разность также интегрируемы на этом отр, причём

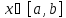4) если ф-ия f(x) интегрир-ая на отр [a;b],где a<b и f(x), т.е. ф-ия «+» для всех х , тогда

5) если f(x) и ф-ии интегрир-ые на отр [a;b], где a<b и f(x) для всех х, , тогда

6) если ф-ия f(x) интегрир-ая на отр [a;b],где a<b, то ф-ия также интегрируемв на [a;b], причём

30 Ф-ла Ньютона-Лейбница

Связь между опред и неопред интегралом выражает след Т: опред интегр от непрерывной ф-ии =разности знач-й любой её первообр-й для верхн и нижн предела интегрирования . Док-во: рассм интегр с переменной верхн пределом: Ф(х)=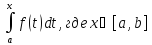, в кот– непрерывно, Ф`(х)=f(x). Пусть F(x) – первообр-е ф-ии f(x). т.е. F`(x)= f(x). Итак ф-ии Ф(х)и F(x) имеют одинаковые производ-е на основании св-ва первообр заключаем что Ф(х)= F(x)+С. Поскольку F(а)=0, при х=а из послед рав-ва получаем 0= F(x)+С, откуда С=- F(а). Ф(х)=F(x)- F(а).

, где F`(x)= f(x). В частности при х=b - ф-ла Ньютона-Лейбница.

Напр

31 Несобств интегралы. Интегралы с бесконечными пределами

При введении понятия опред интегр предполаг-сь, что выполн-ся усл: 1) пределы интегрир-ия а и b явл конечными; 2) подинтегр ф-ия f(x) ограничена на [a;b]. В этом случае опред интегр наз собственным. Если хотя бы одно из усл не выполн-ся, то интегр наз несобств.

Пусть ф-ия у=f(x) непрерывна при любом x>a. Рассм интегр с переменным весрзн пределом. I(b)= (1) как было показано ранее интегр (1) явл диф ф-ей верхн предела. Предположим, что при b ф-ия (1) имеет конечн предел; этот предел наз сходящимся несобств интегр от ф-ии по промеж от [a; +и обозн-сяЕсли этот предел не сущ или =, то несобств интегр назрасходящимся.

Геом несобств интегр от неотрицат ф-ии выраж-т площадь криволин трапеции, ограниченная сверху гр-ка ф-ииу=f(x), слева отр прямой х=а, снизу осью О_х ( в случае сходящегося интегр площадь явл конечн, в случае расходящ-ся . Аналогично определ-ся несобств интегр с нижним пределом. И несобст интегр с обоимипределами, где с – любая точка из (-).

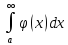Приведём без док-ва 2 теор, с их помощью можно исслед-ть вопрос о сходимости некот несобств интегр. Т1: если при ха выполн-ся нерав-восход-ся то сход-ся и. Причёмрасх-ся то и расх-ся.

Т2: если в промеж [a; +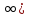ф-ияу=f(x) меняет знак и cход-ся, то сход-ся и

32 Интегр от неограниченных ф-ий

Если ф-ия у=f(x) неограниченна в окрестностях точки С из отр [a;b]и непрер при , то несобств интегр от этой ф-ии опред-ся след обр: (2) где. В случае с=b или с=а получаем (3) или(4). Несобст интегр (3) или (4) наз сходящ-ся, если сущ конечн предел соответств-го опред интегр, в противном случае интегр наз расход-ся. Несобств интегр (2) наз сходящ-ся если сущ и конечн оба предела в правой части. Для интегр от неогран-ых ф-ий справедливы теор аналогичны теор о сходимости некот несобств интегр, они примен-ся для исслед-ия вопроса о сходим-ти несобств интегр и оценки их значений. В кач-ве ф-ий с кот сравнивают подинтегр ф-ию часто выбираютЛегко видеть чтосход-ся при, расх-ся при. Например: исслед-ть сход-ся ли, х=0. Подинтегр ф-ия не ограничена в окрест-ти точки х=0.и;cход-ся , сход-ся и исходный интегр.