7 Действия над матрицами

Линейные действия над матрицей – сложение и вычитание матриц, умножение матриц на число.

Сложение м вычитание матриц определены только для матриц одинаковых размеров.

Суммой двух матриц A=(a_ik)_mn и B=(b_ik)_mn называется такая матрица C=(c _ik)_mn, что c _ik=a_ik+b_ik (i=1,2,3….m; k=1,2,3….n), т. е. матрица, элементы которой равны суммам соответствующих элементов матрицы слагаемых. Сумма двух матриц A и B обозначается A+B.

Под суммой A+B+C трёх матриц A,B,C понимается матрица, полученная в результате последовательного сложения этих матриц, т. е. A+B+C=(A+B)+C. Аналогично определяется сумма матриц для большого числа слагаемых.

Разностью A-B двух матриц A=(a_ik)_mn и B=(b_ik)_mn называется матрица D, такая что d _ik=a_ik+b_ik.

Произведением матрицы A=(a_ik)_mn на число α называется матрица B=(b_ik)_mn, для которой b_ik= α a_ik (i=1,2,3….m; k=1,2,3….n), т. е. матрица, полученная из данной умножением всех её элементов на число α. Обозначается

A α или α A.

Матрицу (-1)A будем называть матрицей, противоположной матрице A и обозначать –A.

Умножение матриц.

Это действие определяется для согласованных матриц.

Матрица A называется согласованной с матрицей B, если число столбцов матрицы A равно числу строк матрицы B. (Матрица A_mn согласована с матрицей B_nl – «ширина» матрицы A= «высоте» матрицы B).

Следует отметить, что:

--Из согласованности матрицы A с матрицей B не следует согласованности матрицы B с матрицей A.

--Если A и B квадратные матрицы одного порядка, то они взаимносогласованы, матрица A согласована с матрицей B, матрица B согласована с матрицей A.

Произведением матрицы A_mn =(a_ik)_mn на матрицу B_nl=(b_ik)_nl называется C_ml=(c _ik)_ml, для которой

c_ik=a_i1b_1k + a_i2b_2k+….+ a_inb_nk, т. е. c_ik матрицы C_ml равен сумме произведений элементов i-той строки матрицы A_mn на соответствующие элементы k-атого столбца матрицы B_nl

Матрица C_ml имеет m строк (как матрица A_mn) и l столбцов (как матрица B_nl)

8 Определители второго и третьего порядка

Определителем квадратной матрицы 2-ого порядка A = называется число, равное -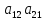и обозначается символом, т. е.=-.

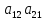Определитель матрицы называется также детерминантом.

Для определителя матрицы A используются следующие обозначения 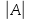,,detA, det(ajk).

Определителем квадратной матрицы третьего порядка A=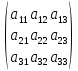называется число, равное=+.

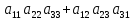Заметим, что каждое слагаемое алгебраической суммы правой части данной формулы представляет собой произведение элементов определителя, взятых по одному и только одному из каждой строки и каждого столбца.

Этому произведению прописывается соответствующий знак. Чтобы запомнить что с +, а что с -, полезно следующее правило.

ПРАВИЛО ТРЕУГОЛЬНИКА.

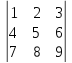=1*5*9+2*6*7+4*8*3-3*5*7-2*4*9-6*8*1.

Минор- определитель, полученный с данного вычёркиванием той строки и того столбца, которым принадлежит данный элемент. Минор элемента a_jk обозначается M_jk. Алгебраическое дополнение элемента a_ik определителя называется его Минор, взятый со знаком (-1)^i+k. Алгебраическое дополнение элемента a_ik будем обозначать A_ik. В соответствие с определителем A_ik=(-1)^i+k M_ik

ТЕОРЕМА. Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраическое дополнение.