
Физика
.pdfS = Lim |
I a |
= |
dI a |
|
mA |
||||
|
|
|
|||||||
U |
|
→0 |
U c dU c |
; (U a |
= Const); |
|
. |
||
|
c |
|
|
B |
|||||
Произведение этих параметров определяет статический коэффициент усиления лампы
μ = Ri S .
Основное применение триода и многоэлектродных электронных ламп – усиление и генерирование электрических колебаний, а также в приемных и передающих устройствах телевидения и других устройствах визуализации быстропротекающих процессов.
Вопросы для самоконтроля
1.Какие вещества называются электролитами?
2.Какие материалы относятся к полупроводникам?
3.Перечислить особенности полупроводников.
4.Устройство полупроводникового диода.
5.Для чего предназначен полупроводниковый триод?
6.В чем заключается явление термоэлектронной эмиссии?
7.Устройство электровакуумного диода.
8.Роль сетки в электровакуумном триоде?
9.Что называется электрическим током?
10.Назвать основные параметры электрического тока.
11.Какие частицы являются носителями заряда в проводниках первого рода?
12.Записать закон Ома для участка цепи.
13.Что называется ЭДС источника тока?
14.Записать закон Ома для замкнутой цепи.
15.В чем заключается закон Джоуля-Ленца?
СПИСОК ЛИТЕРАТУРЫ
Основная
1.Грабовский, Р.И. Курс физики. / Р.И. Грабовский. – 6-е изд – СПБ. : Издательство
«Лань», 2002.- 608 с
2.Пронин, В.П. Краткий курс физики / В.П. Пронин. – Саратов. ФГОУ ВПО «Саратовский ГАУ», 2007 г. – 200 с
Дополнительная
1.Рогачев Н.М. Курс физики. Учебное пособие// С.-Петербург: Издательство «Лань», 2010г.- 448с. 1000 экз.
2.Пронин В.П. Практикум по физике : уч. пособия / В.П. Пронин.- 2-е изд. Пронин В.П. – краткий курс физики. Саратов. СГАУ. 2007 г., 200с.
61
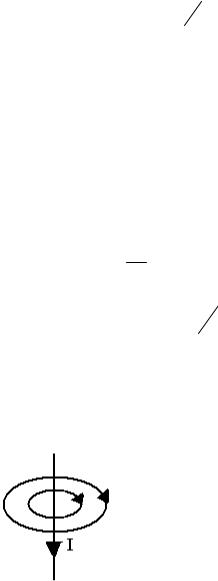
Лекция 7
Магнетизм и электромагнетизм
1.1.Параметры магнитного поля.
Магнитное поле образуется движущимися заряженными частицами или переменным электрическим током.
H - напряженность магнитного поля. Измеряется в A м
R
B - вектор магнитной индукции. Измеряется в Tл
Напряженность магнитного поля и вектор магнитной индукции связаны следующим соотношением:
B= μμ0 H
R
Ф - магнитный поток или поток вектора магнитной индукции.
R
Ф = B × S cosα
α - угол между направлением вектора магнитной индукции и нормалью к плоскости, в которой находится площадь. [Ф] = Вб
μ0 = 4π ×10−7
Гн
м
Напряженность магнитного поля в любой среде выше, чем в вакууме.
Относительная магнитная проницаемость среды μ = H
H 0
Эта величина показывает во сколько раз напряженность магнитного поля в вакууме меньше, чем в любой другой среде (в воздухе=1).
Графически магнитное поле обозначается с помощью линий вектора магнитной индукции (рис.53). Эти линии всегда замкнуты и направление этих линий определяется по правилу Буравчика: рукоятка буравчика, вращаемая по направлению тока, вращается в направлении магнитных силовых линий.
Рисунок 53.
1.2.Основные формулы и законы.
Магнитные свойства вещества обусловлены элементарными круговыми токами.
62
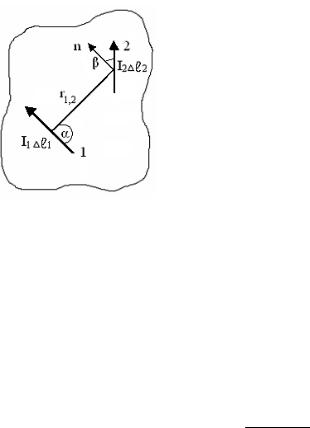
В связи с этим целесообразно изучать магнитные явления через взаимодействия электрических токов. Силу взаимодействия двух проводников с током определил Ампер.
Она зависит от: силы тока в проводниках, от длины проводника, от их взаимного расположения в пространстве, от расстояния между проводниками, от магнитных свойств среды, в которой они находятся.
Закон Ампера.
Рисунок 54.
DF |
= k |
I1I2 × Dl1Dl2 sin α sin β |
|
||
1,2 |
|
r 2 |
|
|
K = μμ0 - коэффициент пропорциональности
4π
Закон Ампера в дифференциальной форме:
dF = μμ0 I1I2 Dl1Dl2 sin α sin β 4πr 2
Закон Био-Савара-Лапласса dH = I1dl1 sin α определяет напряженность магнитного
4πr 2
поля, образованного проводником с током.
α - угол между направляющей силой тока в этом проводнике и направлением на точку, в которой определяется напряженность.
r – расстояние между проводником и точкой, в которой определяется напряженность.
Напряженность магнитного поля, создаваемая проводником с током в любой точке пространства пропорциональна силе тока и длине проводника, и обратно пропорциональна квадрату расстояния от проводника до той точки, в которой определяется напряженность.
Соотношение Био-Савара-Лапласса позволяет рассчитать напряженность магнитного поля, создаваемая проводником любой формы. Для этого нужно геометрически просуммировать напряженности, создаваемые всеми элементарными участками проводника dH.
dH = ∫ dH = |
1 |
∫ |
Ιdl sin α |
|
4π |
r |
2 |
||
l |
l |
|
||
63
Рассмотрим простейшие виды проводников и определим напряженность магнитного поля, создаваемого этими проводниками:
Бесконечно длинный прямой провод H = |
|
I |
; |
I – |
сила тока в проводнике |
||||
|
|
|
|||||||
|
I |
|
|
2πr |
|
|
|||
Кольцевой ток H = |
; r – радиус кольца |
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
2r |
|
|
|
|
|
|||
Катушка с током (соленоид) H = |
I × n |
; |
n |
– количество витков, l – длина |
|||||
|
|||||||||
|
|
|
|
l |
|
|
|
|
|
соленоида
1.3. Действие магнитного поля на проводник с током.
Так как вокруг проводника с током существует магнитное поле, то внешнее магнитное поле вступает во взаимодействие с собственным магнитным полем проводника. Таким образом, на проводник с током, помещенный во внешнее магнитное поле, действует со стороны этого поля сила, называемая силой Ампера.
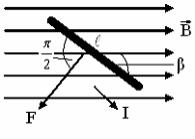
Проводник с силой тока I и длиной l помещен во внешнее магнитное поле с индукцией В (рис.55). На этот проводник действует сила Ампера, направление которой определяется по правилу левой руки.
Получим выражение для силы Ампера. |
|
|||||
Подставим выражение dH = |
Idl sin α |
в закон Ампера в дифференциальной форме, |
||||
|
||||||
|
4πr 2 |
|
|
|
||
получим: |
μμ |
0 4πΙ1Ι |
2 dl1dl2 sin α sin β |
|||
dF1,2 = |
||||||
|
|
|
4πr 2 |
|||
|
|
|
|
|
||
dF = μμ0 dHΙ 2 dl2 sin β B = μμ0 H
Получили формулу Ампера, которая определяет силу, с которой внешнее магнитное поле действует на проводник с током.
Рисунок 55.
F = IBl sin β - формула Ампера
Ðβ - угол между направлением силы тока в проводнике и вектором магнитной поле индукции.
1.4 Виды магнетиков. Гистерезис.
Все вещества по своим магнитным свойствам делятся на три класса:
64
a.диамагнетики ( μ <1, ослабляют внешнее магнитное поле, F, S, C, сурьма)
b.парамагнетики ( μ >1, усиливают внешнее магнитное поле, Al, W, Pt,
щелочно-земельные металлы)
c.ферромагнетики (незначителен, μ >>1(значительно больше 1), значительно
усиливают внешнее магнитное поле, Ni,Co).
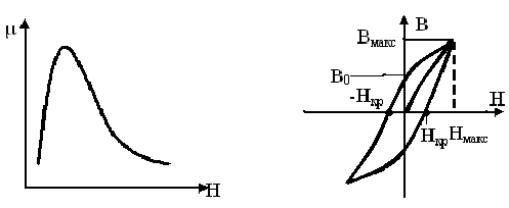
Значимость μ от напряженности внешнего магнитного поля dH не линейная (имеет
экстремум) (рис. 56 а), в связи с этим у ферромагнетиков наблюдается явление гистерезиса.
а). |
б). |
Рисунок 56.
Явление гистерезиса заключается в отставании изменения вектора B от изменения напряженности магнитного поля Н (рис.56 б).
Если площадь петли гистерезиса для материала большая, то говорят о магнитожестких материалах, которые применяются для изготовления постоянных магнитов, а если маленькая – то о магнитомягких, применяемых, например, при изготовлении трансформаторов, статоров и роторов электрических машин.
1.5. Явление электромагнитной индукции. Закон Фарадея.
Явление возникновения ЭДС в замкнутом контуре под действием переменного магнитного потока, пронизывающего этот контур называется электромагнитной индукцией. Это явление было открыто английским физиком Фарадеем.
Закон Фарадея.
ЭДС индукции, возникающая в замкнутом контуре, под действием внешнего магнитного поля, пропорциональна скорости изменения магнитного потока, пронизывающий это контур.
ξ |
i |
= − Ф |
|
t |
|
|
|
Правило Ленца.
Возникающая ЭДС в замкнутом контуре, создает в нем электрический ток такого направления, что его собственное магнитное поле препятствует изменению внешнего магнитного поля.
Согласно правилу Ленца, в законе Фарадея необходимо ставить знак “–“.
65
Ток, который возникает в замкнутом контуре, под действием изменения внешнего магнитного поля называется индукционным.
Закон Фарадея лежит в основе работы генератора переменного тока.
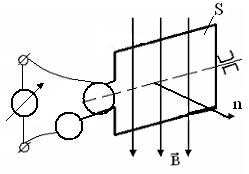
1.6.Получение переменного тока
Если относительно магнитного поля перемещать проводник, то вследствие электромагнитной индукции в нем возникает ЭДС.
Рисунок 57.
Пусть проводник выполнен в виде рамки, которая имеет площадь S и может вращаться вокруг оси перпендикулярной однородному магнитному полю (В=Const). Контур пронизывается магнитным потоком (рис.57)
Ф = ВSCos α = dSCos ωt ,
где α =ωt угол между направлением вектора магнитной индукции и нормалью к плоскости расположения рамки.
При вращении рамки поток вектора магнитной индукции, пронизывающий контур, периодически изменяется и согласно закону Фарадея возникает ЭДС индукции
ξ = − |
dΦ |
= BS ω Sin ω t = ξ |
макс Sin ω t . |
|
|||
|
dt |
|
|
То есть в контуре проводника возникает переменная электродвижущая сила, изменяющаяся по закону синуса.
В замкнутой цепи возникает переменный ток
I = |
ξ |
= |
ξ макс |
Sin ω t = I |
макс Sin ωt , |
R |
|
||||
|
|
R |
|
||
Сила тока и напряжение переменного тока изменяются синусоидальному и конусоидальному законам, а направление переменного тока в следствии правила Ленца изменяется на противоположное.
1.7.Явление взаимной индукции и самоиндукции.
Частным случаем явления электромагнитной индукции являются явления взаимной индукции и самоиндукции.
66
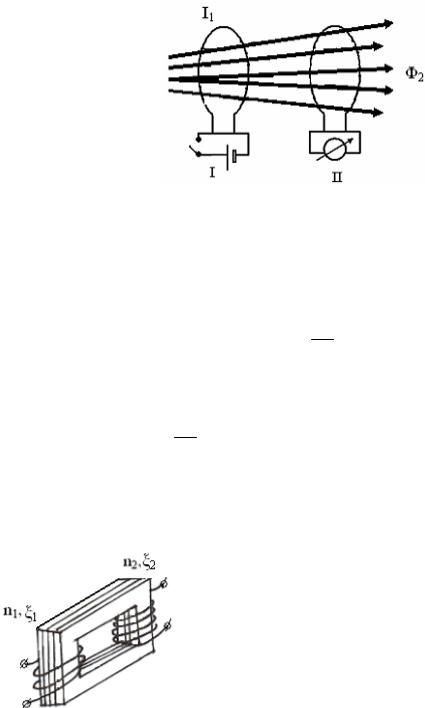
Рисунок 58.
Взаимная индукция – это явление возникновения ЭДС в замкнутом контуре при изменении тока в соседнем контуре. Пусть в замкнутом контуре I существует переменный ток (рис. 58). Возникающее вокруг этого контура магнитное поле пронизывает соседний замкнутый контур. Так как магнитный поток, пронизывающий этот контур изменяется, то в нем будет возникать ЭДС, определяемая по формуле:
ξ 2 = −M dΙ1 dt
M – коэффициент взаимной индукции.
Явление возникновения ЭДС в замкнутом контуре при изменении тока в этом же контуре называется самоиндукцией.
ξ = −L dΙ1 где, L – коэффициент самоиндукции. dt
Явление взаимной индукции лежит в основе работы трансформатора, устройства, предназначенного для повышения или понижения входящего напряжения.
Трансформатор состоит из двух или нескольких катушек с разным количеством витков. Катушки намотаны на ферромагнитный сердечник.
Рисунок 59.
На первичную катушку подается переменное напряжение. Образованное вокруг нее магнитное поле пронизывает витки вторичной катушки, в которой вследствие взаимной индукции возникает ЭДС, порождающая ток. Количество витков на вторичной катушке пропорционально силе индукционного тока.
k – Коэффициент трансформации.
k = |
n2 |
= |
E2 |
если, k>1 – трансформатор повышающий |
|
n1 |
E1 |
||||
|
|
|
67

k<1 – трансформатор понижающий
Ферромагнитный сердечник состоит из отдельных пластин, изолированных друг от друга, чтобы избежать вихревых токов.
1.8. RLC - цепь
Рассмотрим цепь переменного тока, состоящую из резистора, конденсатора и катушки индуктивности.
Пусть приложено переменное напряжение.
Резистор в цепи переменного тока:
R
U = U 0 sin wt
U 0 − амплитуда колебаний
w - круговая частота t − время
Ι = |
U |
= |
U 0 |
sin wt |
= Ι |
|
sin wt |
|
R |
|
|
R |
0 |
||||
|
|
|
|
|
|
|
||
На резисторе колебания силы тока и напряжения совпадают по фазе:
U R = U 0 sin wt
I R = I 0 sin wt
Сопротивление резистора в цепи переменного тока называется активным. В других случаях этого не происходит.
Конденсатор в цепи переменного тока:
На конденсаторе и на катушке индуктивности колебаний I и U не совпадают по фазе, поэтому сопротивление конденсатора и катушки называется реактивным.
Конденсатор в цепи постоянного и переменного тока ведет себя по-разному. В цепи постоянного тока он обладает бесконечно большим сопротивлением. В цепи же переменного тока конденсатор обладает ёмкостным сопротивлением.
Сопротивление конденсатора в цепи переменного тока.
Пусть задано переменное напряжение:
U = U 0 sin wt
По определению силы тока:
68
|
I = |
dq |
= |
d (CИ) |
= |
dC ×U 0 sin wt |
= CU |
0 w cos wt |
C = |
q |
q = Cϕ = CU |
|
dt |
dt |
dt |
ϕ |
|||||||
|
|
|
|
|
|
|
|
||||
I = I cos wt |
|
|
|
|
|
|
|
|
|||
U c |
− напряжение на конденсаторе |
|
|
|
|
|
|||||
U c |
= U 0 sin wt |
|
|
|
|
|
|
|
|||
Ι c = Ι 0 cos wt
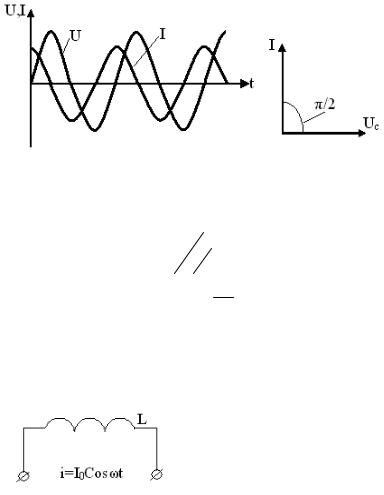
Фазы колебаний силы тока и напряжения на емкости различны и отличаются на
Ðπ . (рис.60) 2
Рисунок 60.
Напряжение на конденсаторе отстает от силы тока.
I0 = СU 0 w
I0 = U 0 |
1 |
сопротивление на конденсаторе |
|
wc |
|
|
|
X c = 1 емкостное сопротивление wc
Катушка индуктивности в цепи переменного тока.
Рассмотрим катушку индуктивности в цепи переменного тока. Получим сопротивление этой катушки.
Пусть по цепи протекает переменный ток:
I = I0 сoswt
по определению самоиндукции имеем:
ξc |
= -L |
dI |
= -L |
dI 0 |
cos wt |
= LI |
|
sin wt × w = LI0 wsin wt = ξ0 sin wt |
dt |
|
dt |
0 |
|||||
|
|
|
|
|
|
|
||
ξ = ξ0 sin wt |
|
|
|
|
|
|||
U L |
= U 0 sin wt |
|
|
|
|
|
||
I L |
= I 0 cos wt |
|
|
|
|
|
||
69
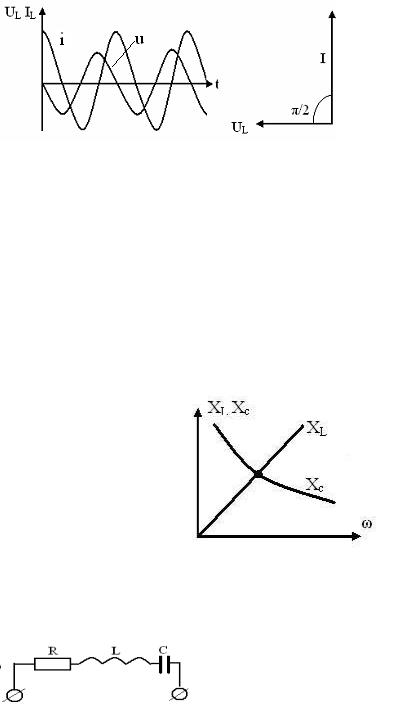
Колебания силы тока и напряжения на катушке индуктивности не совпадают по
фазе, а отличаются на Ð π , катушка обладает реактивным сопротивлением, но в
2
отличие от конденсатора здесь напряжение опережает силу тока (рисунок 61).
Рисунок 61.
|
|
|
|
ξ0 = LI0 w |
U 0 |
= LI 0 w I 0 |
= |
U 0 |
- индуктивное сопротивление X L обозначает: |
|
||||
|
|
|
Lw |
|
X L = wL - сопротивление на катушке индуктивности
Зависимость индуктивного и емкостного сопротивления от частоты тока.
Из формул для расчета емкостного и индуктивного сопротивлений видно, что емкостное сопротивление изменяется обратно пропорционально круговой частоте, а индуктивное сопротивление – прямо пропорционально, что отражено на графике зависимости индуктивного и емкостного сопротивлений от частоты переменного тока
( рис.62)
Рисунок 62.
Рассмотрим последовательную цепь переменного тока, содержащую резистор, конденсатор и катушку индуктивности(рис.63)
Рисунок 63.
U = U R + U c + U i равно сумме на отдельных ее участках, а ток один и тот же.
70
