5. Классификация точек разрыва

Определение. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Если — точка разрыва функции , то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:

• Функция определена в окрестности точки , но не определена в самой точке . Например, функция 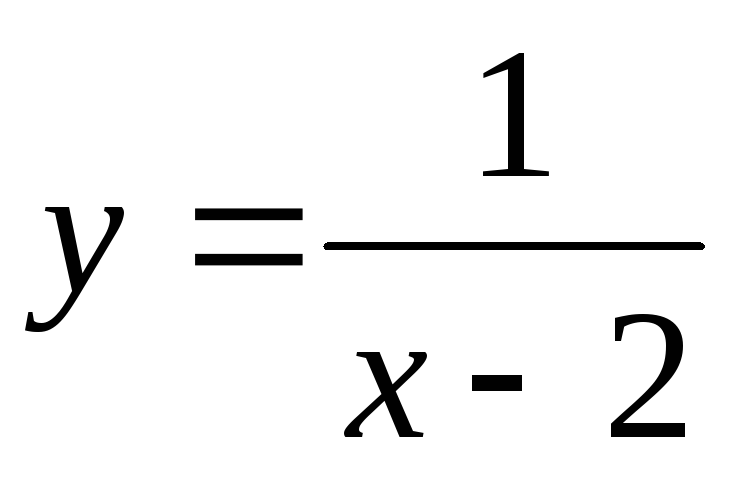не определена в точке (рисунок 26).

• Функция определена в точке и её окрестности, но не существует предела при .

Например, функция

определена в точке ( f (2) = 0), однако в точке имеет разрыв (рисунок 27), т.к. эта функция не имеет предела при :

.

• Функция определена в точке и её окрестности существует но этот предел не равен значению функции в точке : .

Например, функция (рисунок 28). Здесь – точка разрыва, т.к а

В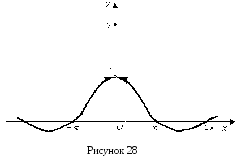се точки разрыва функции разделяются на точки разрыва первого и второго рода.

Определение. Точка разрыва называется точкой разрыва первого рода функции , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т. е. и . При этом:

а) если , то точка называется точкой устранимого разрыва;

б) если , то точка называется точкой конечного разрыва. Величину называют скачком функции в точке разрыва первого рода.

Точка разрыва называется точкой разрыва второго рода функции , если по крайней мере один из односторонних пределов (слева, или справа, или оба вместе) не существует или равен бесконечности.

Обратимся к функциям, рассмотренным выше.

Для функции , — точка разрыва второго рода (рисунок 26).

Для функции является точкой разрыва первого рода (рисунок 27), скачок функции равен

Для функции 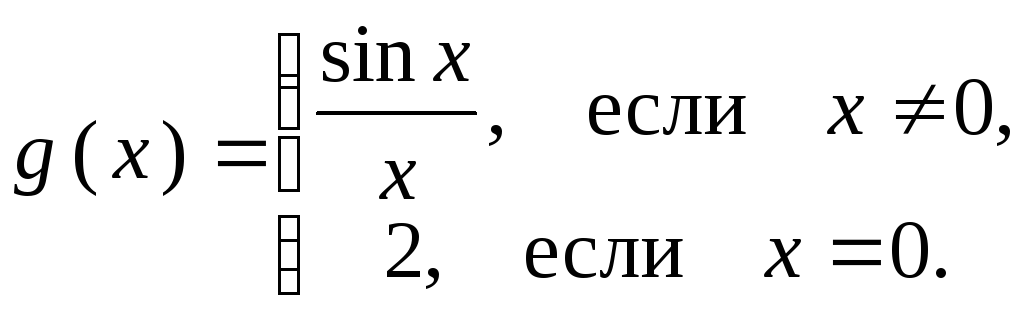является точкой устранимого разрыва первого рода (рисунок 28). Положив (вместо ) при , разрыв устранится, функция станет непрерывной.

Пример Дана функция . Найти точки разрыва, выяснить их тип.

Решение. Функция определена и непрерывна на всей числовой оси, кроме точки . Очевидно,

Следовательно, , а Поэтому в точке функция имеет разрыв первого рода. Скачок функции в этой точке равен

Основные теоремы о непрерывных функциях Непрерывность элементарных функций

Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах. Приведем их тоже без доказательства

Теорема 5.16Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).

Теорема 5.17 Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция , состоящая из непрерывных функций, непрерывна в точке .

Теорема 5.18 Если функция непрерывна и строго монотонна на оси Ох, то обратная функция также непрерывна и монотонна на соответствующем отрезке оси Оу .

Например, функция , в силу теоремы 3.16, есть функция непрерывная для всех значений х, кроме тех, для которых , т.е. кроме значений . Функции , в силу теоремы 3.18, непрерывны при всех значений х при которых эти функции определены.

Теорема 5.19Все основные элементарные функции непрерывны при всех значениях х, для которых они определены.

Как известно, элементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. Поэтому из приведённых выше теорем вытекает:

Теорема 5.20 Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.

ПримерНайти

Решение. Функциянепрерывна в точке, поэтому