Основные свойства функций

1. Функция y = f (x), определённая на множестве D, называется чётной, если 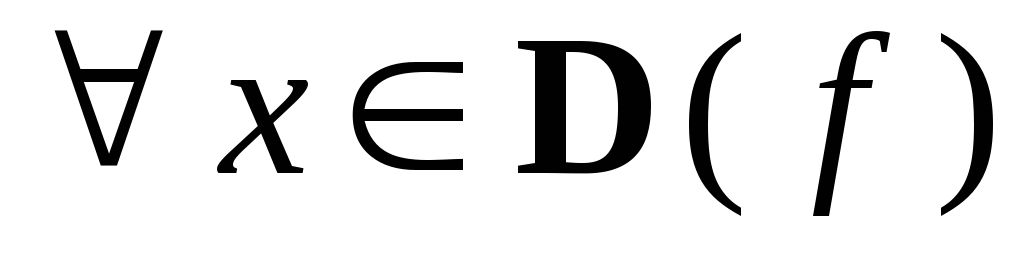выполняется условие и

.

График чётной функции симметричен относительно оси Оу (рисунок 2).

Примеры чётных функций:

(рисунок 10), (рисунок 13).

2. Функцияy = f (x), определённая на множестве D, называется нечётной, если выполняется условие и

.

График нечётной функции симметричен относительно начала координат (рисунок 3).

Примеры нечётных функций:

(рисунок 10), (рисунок 13) (рисунок 14).

Область определения четной и нечетной функции симметрична относительно начала координат. Если это условие не выполнено, то функция не может быть ни четной, ни нечетной.

3. Функция называется периодической, если существует такое положительное число Т, что для выполняется равенство

при этом число Т называют периодом функции.

Если Т – период функции , то и пТ – также есть период этой функции, п  Z. Число Т при этом называют основным или наименьшим периодом функции.

Г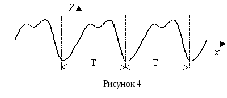рафик периодической функции на любых двух соседних отрезках оси ОХ длины Т имеет один и тот же вид (рисунок 4).

Периодическими являются тригонометрические функции:

с периодом T = 2; с периодом T = .

Для функций , период равен , а для , период равен .

Если периодические функции и имеют соизмеримые периоды Т₁ и Т₂, т.е. такие, что пТ₁ = тТ₂, где п и т – некоторые целые числа, то они имеют общий период Т = пТ₁ = тТ₂.

Если периодические функции и имеют один и тот же период Т, то функции и , где А и В – любые числа, также будут периодическими с периодом Т.

Если периоды функций и несоизмеримы, то функция – не периодическая.

4. Функция 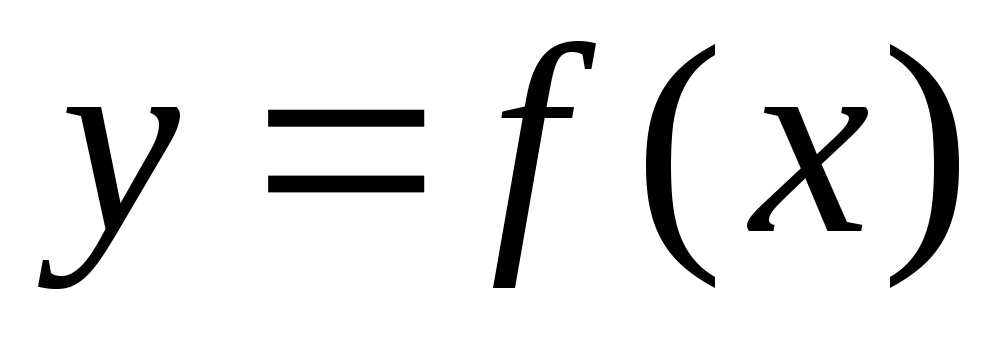называется возрастающей на множестве , если большему значению аргумента соответствует большее значение функции, т.е. для любых 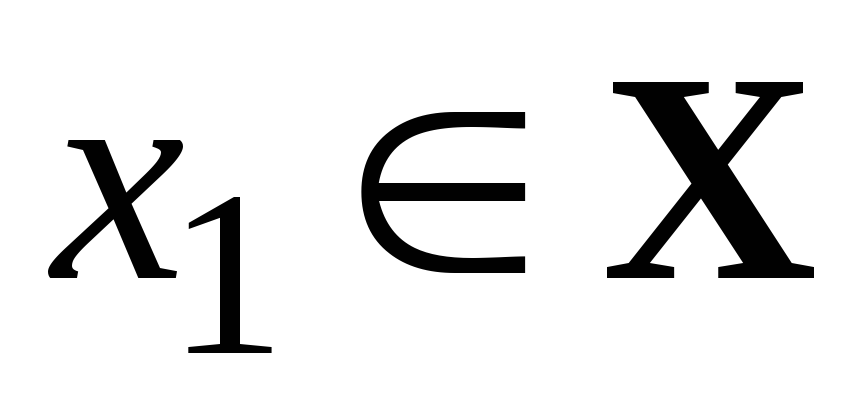, , 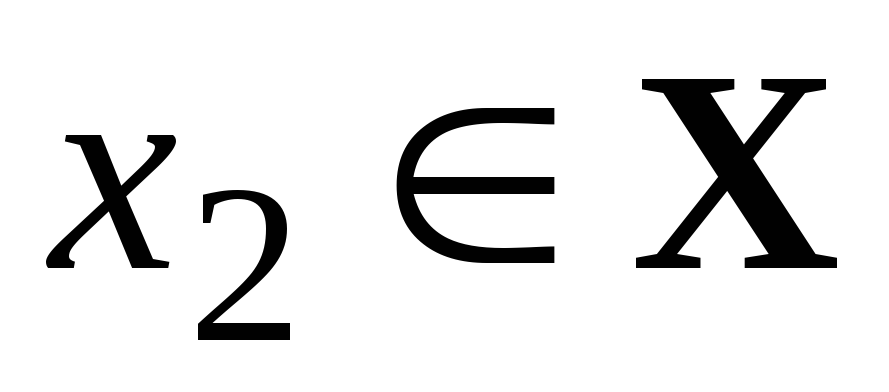таких, что 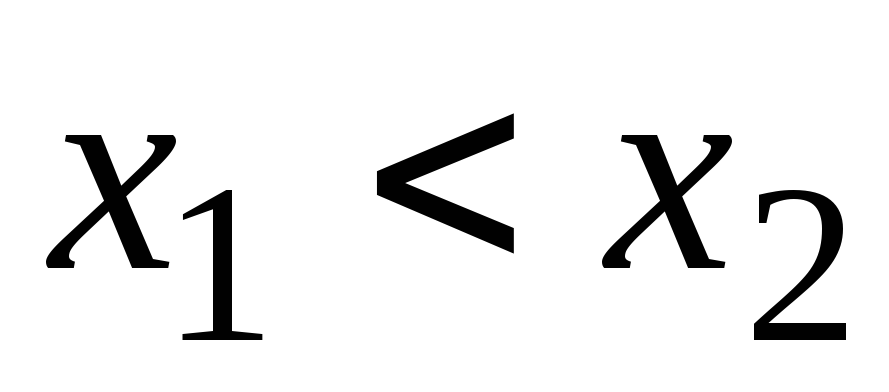, выполняется неравенство (рисунок 5, а).

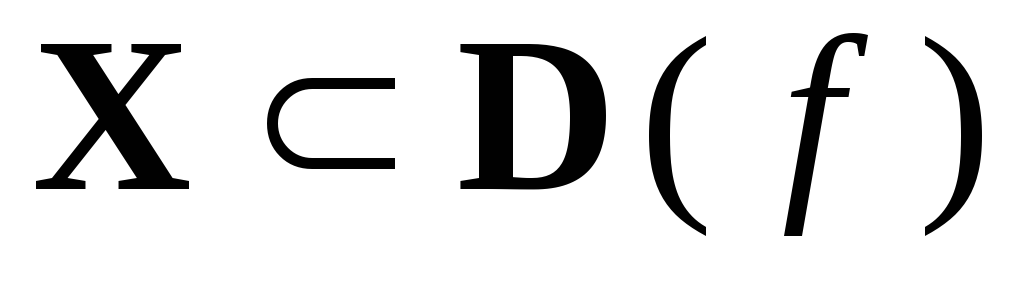5. Функция называется убывающей на множестве , если большему значению аргумента соответствует меньшее значение функции: для любых 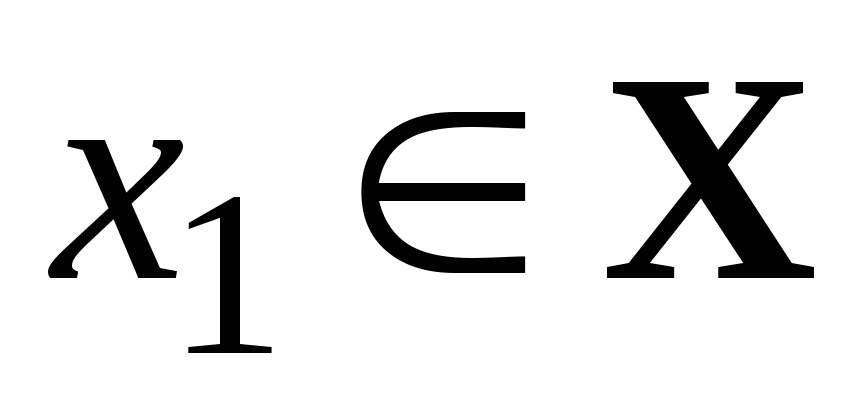, , (рисунок 5, б).

6. Функция называется ограниченной на множестве , если существуют такие числа А и В, что для всех выполняется условие

.

Геометрически это означает, что график функции расположен в некоторой горизонтальной полосе между прямыми у = А и у = В. (рисунок 6)

Ограниченными в своей области определения являются функции и , т.к. для всех значений х выполняется и

Если для всех значений выполняется неравенство , то функция ограничена сверху на множестве Х (рисунок 7, а). Если же , то функция ограничена снизу (рисунок 7, б).

Примером ограниченной снизу функции служит показательная функция т.к. для всех действительных значений х значения .

Обратная функция

Пусть функция с областью определения D и множеством значений E такова, что двум разным значениям аргумента ставит в соответствие разные числа, т.е. для любых

Это означает, что функция принимает каждое своё значение у  E только при одном значении аргумента х D, т.е. функция задаёт между множествами D и E взаимно однозначное соответствие.

Геометрически это отражается в том, что любая прямая, параллельная оси Ох, пересекает график функции только один раз (рисунок 8).

Определение. Если каждому значению у  E поставить в соответствие число х такое, что , то на множестве E будет определена функция, которая называется обратной для функции и обозначается Функция при этом называется обратимой, а функции f и называются взаимно обратными.

Чтобы найти функцию , обратную к функции , достаточно решить уравнение относительно х (если это возможно). Например, для функции у = 2х + 3 обратная функция определяется формулой .

Функция, заданная одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операции взятия функции от функции, называется элементарной функцией.

Примерами элементарных функций могут служить функции

и т.п.