100

Тема5 . Введение в математический анализ Множество действительных чисел. Последовательности

Понятие множества является одним из основных неопределяемых понятий математики. Под множеством понимают совокупность (собрание, класс, семейство …) некоторых объектов, объединённых по какому либо признаку. Так можно говорить о множестве студентов университета, о множестве рыб в Чёрном море, о множестве корней уравнения , о множестве всех натуральных чисел и т.д.

Объекты, из которых состоит множество, называются его элементами. Множества пронято обозначать заглавными буквами латинского алфавита A, B, …, X, Y, …, а их элементы — малыми буквами a, b, … , x, y, …

Если элемент х принадлежит множеству Х, то записывают ; запись или означает, что элемент х не принадлежит множеству Х.

Множество, не содержащее ни одного элемента, называется пустым и обозначается символом .

Элементы множества записываются в фигурных скобках, внутри которых они перечисляются (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества. Например, запись означает, что множество А состоит из трёх чисел 1, 3, и 15; запись означает, что множество А состоит из всех действительных (если не оговорено иное) чисел, удовлетворяющих неравенству 0  х  2.

Множество А является подмножеством множества В, если каждый элемент множества А является элементом множества В. Символически это обозначается А  В («А включено в В») или В  А («множество В включает в себя множество А»).

Говорят, что множества А и В равны или совпадают, и пишут А = В, если А  В и В  А. Другими словами, множества, состоящие из одних и тех же элементов, называются равными.

Определение. Объединением (или суммой) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств Объединение (сумму) множеств обозначают А  В (или А + В). Кратко можно записать А  В =  х : х  А или х  В.

Определение. Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Пересечение (произведение) множеств обозначают А  В (или А  В). Кратко можно записать А  В =  х : х  А и х  В.

В дальнейшем для сокращения записей будем использовать некоторые простейшие логические символы:

   — означает « из предложения  следует предложение »;

   — «предложения  и  равносильны», т.е. из  следует  и из  следует ;

 — означает «для любого», «для всякого» ;

 — «существует», «найдётся»;

 — «имеет место», «такое, что»

Например, запись  х  А   — означает «для любого элемента х А следует предложение », или ( х  А  В)  ( х  А или х  В) определяет объединение множеств А и В, или запись — означает « найдётся такое число N, что для любого натурального числа n следует предложение ».

Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:

N = {1; 2; 3; …; n;…}  множество натуральных чисел;

Z₀ = {0; 1; 2; 3; …; n;…}  множество целых неотрицательных чисел;

Z = {0; 1; 2; 3; …; n;…}  множество целых чисел;

Q = множество рациональных чисел;

R  множество действительных чисел.

Между этими множествами существует соотношение

Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью, или бесконечной периодической дробью. Так,  рациональные числа.

Действительные числа, не являющиеся рациональными, называются иррациональными. Иррациональное число выражается бесконечной непериодической дробью. Так,  иррациональные числа. Можно сказать: множество действитьельных чисел есть множество всех бесконечных десятичных дробей. И записать

Множество R действительных чисел обладают следующими свойствами.

Оно упорядоченное: для любых двух различных чисел a и b имеет место одно из двух соотношений либо .

Множество R плотное: межде любыми двумя различными числами a и b содержится бесконечное множество действительных чисел х, т.е. чисел, удовлетворяющих неравенству . Так если , то одним из них является число , так как из a < b  2a < a + b и a + b < 2b  2a < a + b < 2b  a < < b.

Множество R непрерывное. Пусть множество R разбито на два непустых класса A и B таких, что каждое действительное число содержится только в одном классе и для каждой пары чисел а  A и b  B выполнено неравенство . Тогда (свойство непрерывности) существует единственное число с, удовлетворяющее неравенству a  с  b (а  A и b  B). Оно отделяет числа класса А от чисел класса В. Число с является либо наибольшим числом в классе А (тогда в классе В нет наименьшего числа), либо наименьшим числом в классе В (тогда в классе А нет наибольшего числа).

Свойство непрерывности позволяет установить взаимноодноз-начное соответствие между множеством всех действительных чисел и множеством всех точек прямой. Это означает. Что каждому числу х  R соответствует определённая (единственная) точка числовой оси и, наоборот, каждой точке оси соответствует определённое (единственное) действительное число. Поэтому вместо слова «число» часто говорят «точка».

Пусть а и b  действительные числа, причём a < b.

Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:

отрезок (сегмент, замкнутый промежуток);

интервал (открытый промежуток);

и  полуоткрытые интервалы (или полуоткрытые отрезки);

бесконечные интервалы (промежутки).

Числа a и b называются соответственно левым и правым концами этих промежутков. Символы  и  не числа, а символическое обозначение процесса неограниченного удаленияточек числовой оси от начала 0 влево и вправо.

Пусть  любое действительное число (точка на числовой прямой).

Определение. Окрестностью точки называется любой интервал (a; b), содержащий точку. В частности, интервал (  , + ), где   0, называется окрестностью точки . Число называется центром, а число   радиусом (рисунок 1).

З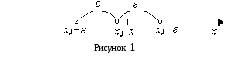амечание. Расстояние между двумя точками х и на числовой оси (рисунок 3.1) равно абсолютной величине разности чисел х и :

Если х  (  , + ), то выполняется неравенство   < x < + , или, что одно и то же, . Оба эти неравенства означают попадание точки х в окрестность точки (рисунок 1).