Методы вычисления Численные методы решения задач математической физики
Точные и итерационные методы решения систем линейных алгебраических уравнений. Метод квадратных корней. Метод Халецкого. Методы итераций и Зейделя.
Нахождение максимального по модулю собственного значения и соответствующего собственного вектора матрицы. Итерационный метод.
Итерационные методы решения нелинейных и трансцендентных уравнений. Методы итерации, секущих и Ньютона.
Интерполяция функции. Интерполяционные формулы Лагранжа. Ньютона. Остаточные члены.
Численные интегрирование. Квадратурная формула Ньютона – Котеса. Формула Симпсона и ее остаточный член.
Аппроксимация дифференциальных операторов.
Метод прогонки решения краевой задачи для обыкновенного дифференциального уравнения второго порядка.
Явные и неявные схемы и схемы с весами для уравнения теплопроводимости. Аппроксимация и устойчивость. Сходимость.
Схемы с весами для уравнения колебаний. Аппроксимация и устойчивость. Сходимость.
Явный метод установления решения разностной задачи Дирихле для уравнения Пуассона. Условия сходимости. Простейшая двухслойная схема переменных направлений.
Теория функций комплексных переменных
Необходимые условия голоморфности функции в точке. Пример.
Достаточные условия голоморфности функции в точке. Пример.
Геометрическая интерпретация модуля и аргумента производной голоморфной функции.
Интегральная теорема Коши в односвязной области. Пример
Доказать, что интеграл от голоморфной в односвязной области функции вдоль любого замкнутого контура равен нулю.
Доказать, интегральную формулу коши.
Показать, что голоморфная функция бесконечно раз дифференцируема
Локальное разложение голоморфных функций в степенные ряды.
Первая теорема Лувилля для целых функций.
Вторая теорема Лувилля для целых функций.
Теоремма Мореры
Доказать теорему разложения голоморфных функций в ряды Лорана
Доказать принцип аргумента
Доказать теорему Руше
Аналитическое продолжение по Коши
Лемма Шварца
Принцип симметрии
Теорема Коши о вычетах
Вывести формулы вычетов для однозначной аналитической функции.
Обозначим через
множество всех отображений вида
.
Показать, что
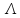образует группу, если в качестве
умножения рассматривать композицию.
Алгебра и аналитическая геометрия
Различные способы задания плоскости. Параметрические уравнения, общее уравнение, уравнение плоскости в отрезках,уравнение плоскости проходящей через три точки и т.д.
Различные способы задания прямой на плоскости. Взаимное расположение двух прямых.
Векторное произведение векторов, свойства. Площадь треугольника. Объем тетраэдра.
Матрица. Деиствия над матрицами. Обратная матрица .различные способы нахождения обратной матрицы.
Различные способы задания прямой в пространстве. Каноническое, параметрическое и общее уравнение прямой в пространстве.
Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью.
Эллипсоид. Гиперболоиды.
Формы записи комплексных чисел. Алгебраическая, полярная (тригонометрическая), показательная (экспоненциальная) формы.
Параболоиды.
Формула Муавра. Извлечение корней из комплексных чисел
Операции над многочленами .Делители. НОК-наибольший общий делитель .
Корни многочленов. Основная теорема. Алгоритм Евклида.
Смешанное произведение векторов, свойства. Геометрический смысл смешанного произведения векторов.
Оределители и его свойства.
Решение слау методом Крамера. Теорема Кронекера- Капелли.
Решение слау методом Гаусса. Теорема Кронекера- Капелли.