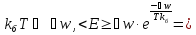- •19. Мікроскопічна теорія Бардіна-Купера-ш. Рівняння бкш для щілини та його нетривіальне рішення.
- •13. Фонони кристалічної гратки, їх характеристики.
- •10. Коливання лінійного ланцюжка атомів різного сорту;
- •2. Кинетическая теория электропродн. И дифузии электронов в тт.
- •7. Кінетичні явища у магнітному полі
- •3. Кінетичне рівняння Больцмана
- •11. Розрахунок температурної залежності теплоємності в моделі Ейнштейна. Температура Ейнштейна
- •12. Розрахунок температурної залежності теплоємності в моделі Дебая. Температура Дебая
- •15. Теплове розширення твердих тіл
- •4. Електропровідність металів
- •9. Коливання лінійного ланцюжка атомів одного сорту;
1. Розподіл Фермі-Дірака для електронів. Енергія Фермі.
Розглянемо ідеальний Фермі-газ, який складаеться з невзаемодіючих електронів. Будемо вважаті також, що електроні не взаемодіють з граткою. Для такого ідеального електроного газу діє формула розподілу електронів Фермі:

Зміст фунції: визначення вірогідності того, що у ансамблі електронів знайдеться електрон з енергіей Е при температурі Т.
Де
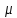 – химический потенциал, який представляе
собою енергію Гіббса,яка приходиться
на одну частинку.
– химический потенциал, який представляе
собою енергію Гіббса,яка приходиться
на одну частинку.
Т – температура
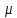 визначаеться
з умови, що повна кількість електронів
у системі дорівнюе N:
визначаеться
з умови, що повна кількість електронів
у системі дорівнюе N:
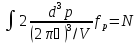
V – обем у К-просторі, який приходиться на один. стан.
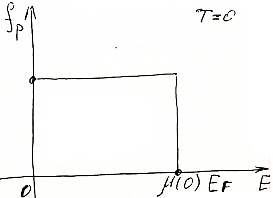
Вигляд функці\ Фермі-Дірака при Т = 0
Перейдемо до сверічніх коордінат і запишемо інтеграл
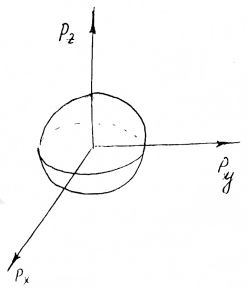
d3p=4πp2 dp
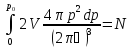
Розраховуючи інтеграл отримаемо граничній імпульс:
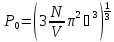
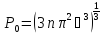 –граничний
імпульс Фермі не залежить від масси
єлектрона і така ситуація зберігаеться
навіть при врахуванні взаемодіїміж
між єлектронами.
–граничний
імпульс Фермі не залежить від масси
єлектрона і така ситуація зберігаеться
навіть при врахуванні взаемодіїміж
між єлектронами.
Енергія електрона(енергія Фермі)
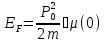
Усі стани при Т=0 менші єнергії Фермі зайняті, а вищі – пусті.
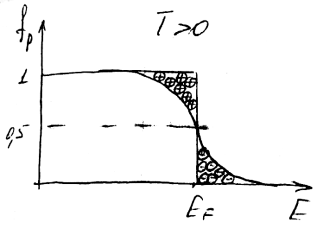
Зявляеться шар електронів над поверхнею Фермі. У провідності напівпровідників приймае участь шар єлектронів вищі енергії Фермі.
Температурна залежність хімічного потенціалу визначаеться по формулі:
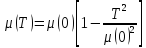
При
зростанні температури хімічний потенціал
зменшуеться. При Т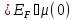 хімічний потенціал
хімічний потенціал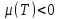 стае відємним
стае відємним
18.Основні принципи мікроскопічної теоріі:
1)між єлектронами надпровідника має місце притягнення в наслідок коливання кристалічної градки.
2)Електрони поблизу рівня Фермі можуть утворювати зв’язні стани – куперовські пари.
А)Фрьоліх довів, що електрони можуть притягуватися одне до одного у 1939р.
Нехай
є 2 електрони з квазіімпульсами
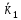 і
і ,
спінами
,
спінами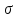 ,
то вони можуть взаємодіяти з кристал.
градки , після цього
,
то вони можуть взаємодіяти з кристал.
градки , після цього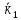 переходить в стан
переходить в стан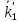 ,а
,а
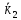 в
в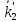 .
.
Поведінка
електронів у кристалі з квазіімпульсами
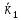 і
і .
.

Електрони можуть взаємодіяти з фононами з імпульсом q
І
етап є 2 електрони з
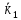 і
і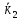 .
.
ІІ
етап
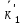 ,q,
,q,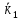 .
.
ІІІ
етап 2 електрони в станах
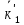 і
і
Розглянемо поляризовану градку в околі електронів.
Градка більш інерційна,ніж електрон підсистеми.
1 електрон поляризує градку, а 2 притягується до цієї поляризації і виходить так ніби 1 електрон притягується до іншого.
Матричний елемент взаємодії електронів:
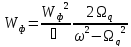
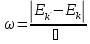 -
частота
яка відповідає різниці енергії в
початковому і кінцевому стані.
-
частота
яка відповідає різниці енергії в
початковому і кінцевому стані.
Знак «-» обумовлений появою притягнення.
Приятяжіння замінює відштовхуваність і утвоює куперівські пари.

І
стан: к1
і к2
і (проміжковий стан)
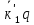 ,
,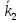 .
.
II
стан кінцевий
 і
і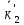
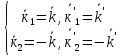
З урахуванням притягнення і кулонівського відштовхування,сумарний матричний елемент такої взаємодії:


,де
 – фрьоліховський елемент, x–величина
зворотня до радіусу
дебаївського екранування.
– фрьоліховський елемент, x–величина
зворотня до радіусу
дебаївського екранування.
Якщо
цей процес явл. пружним, то
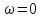 .
.
Маємо притяжнення у чистому вигляді

Б) Куперівські пари
У 1956р. показав, що електрони поблизу поверхні Фермі можуть створювати пари при скіль завгодно малої взаємодії.Такі пари мають спін 0 або 1 і наз. бозонами.
Розрахуємо енергію такої пари:
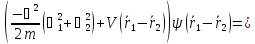
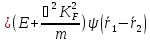
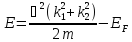
Хвильву функцію шукали у вигляді:
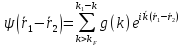
Згідно
з принципом Паулі
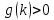 ,
якщо
,
якщо
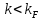 .
.
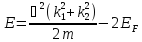 –енергія
куперівської пари, що відраховується
від енергії Фермі.
–енергія
куперівської пари, що відраховується
від енергії Фермі.
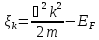 –енергія
одного електрона, що відраховується
від енергії Фермі.
–енергія
одного електрона, що відраховується
від енергії Фермі.
Вирішуємо рівняння і отримуємо:
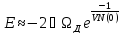 ,
,
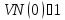
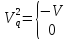 ,
,
 –плотность
електронних состояний на ур. Фермі.
–плотность
електронних состояний на ур. Фермі.
Якщо «-», то має місце притягування і максимальне притягування куперівських пар буде для тв. водорода
т.я.
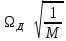 і
чим вище т-ра.
і
чим вище т-ра.
Однак в реальному п/п багато куперівських пар.
19. Мікроскопічна теорія Бардіна-Купера-ш. Рівняння бкш для щілини та його нетривіальне рішення.
Для рішення задачі о системі купера враховують БШК використовують метод вторинного квантування()
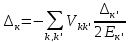 рівняння
БШК для щілини
рівняння
БШК для щілини
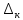 -
одинична щілина,яка утворюется при
переході в надпровідній стан.
-
одинична щілина,яка утворюется при
переході в надпровідній стан.
Рішення:
1)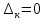
2)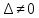
Частка електронів, які можуть зв’язувати в пари,визначается єлек.
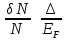
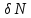 -кількість
єлек. які створюють пари.
-кількість
єлек. які створюють пари.



13. Фонони кристалічної гратки, їх характеристики.
Фонон – квант коливального поля(живе тільки у гратці).
Фонону
у кристалі відповідає квазіімпульс
 ?
Але
оскільки кристал обмежений, то в ньому
існують стоячі хвилі, тобто в умовах
термодинамічної рівноваги не відбувається
переносу імпульсу. Якщо кристал
збуджувати, то зявляються хвилі, які
переносять енергію та імпульс.
?
Але
оскільки кристал обмежений, то в ньому
існують стоячі хвилі, тобто в умовах
термодинамічної рівноваги не відбувається
переносу імпульсу. Якщо кристал
збуджувати, то зявляються хвилі, які
переносять енергію та імпульс.
Вираз для квантового осцилятора:
Е
=
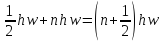
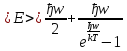
Фонони – бозони з нульовим спіном, які підкоряються статистиці Бозе – Ейнштейна:
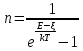
Хімічний
потенціал 𝝃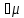 ,
𝝃=0.
,
𝝃=0.
Кількість фононів у стані з частотою wпри температурі Т описується розподілом Бозе-Ейнштейна.
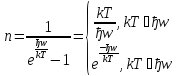
Характеристики фононів:
1.кількість станів фононів, які мають частоту в інтервалі w;w+dw
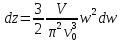
2.кількість фононів у відповідному інтервалі частот
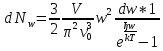
3.енергія фононів у відповідному інтервалі частот
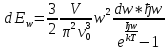
4.повна кількість фононів у кристалі при температурі Т
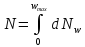
Якщо
позначити
 ,
то
,
то
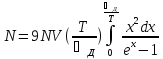
5.сумарна внутрішня енергія кристала

Розглянемо кількість фононів при різних співвідношеннях:
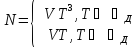
Резюме:
1. Т=0К – вакуум фононів
2.
Т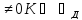 -
ідеальний газ фононів(не взаємодіють)
-
ідеальний газ фононів(не взаємодіють)
3.
Т>> -
неідеальний газ фононів, які взаємодіють
-
неідеальний газ фононів, які взаємодіють
23. Модель Ейнштейна(1911р)
Припущення:
1.Вважав, що для діелектричнихнапівпровідників теплоємністьдає динаміка кристалічн. решітки. Не враховує акустичної гілки дисперсії.

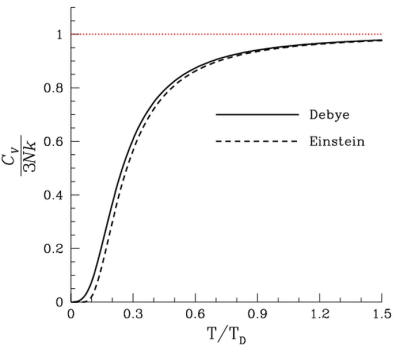
!!!!!Использовать для сравнения!!!!
2.
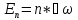 енергія одного атомного осцилятора,
енергія одного атомного осцилятора,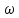 = const
= const
3.
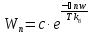 – дисперсія
– дисперсія
4.
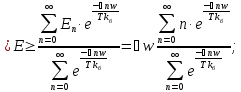
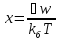

 –середня
енергія одного осцилятора.
–середня
енергія одного осцилятора.
Знайдено значення середньої енергії осцилятора у випадку високих і низьких температур.
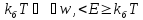 ->
->
 –високі
температури
–високі
температури
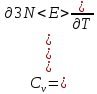 –низькі
температури
–низькі
температури
Загальний
випадок:
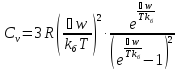

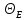 –температура
Ейнштейна.
–температура
Ейнштейна.
10. Коливання лінійного ланцюжка атомів різного сорту;
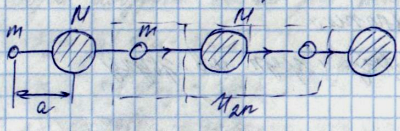
Силові сталі будемо вважати однаковими по обидві частинки атома.
М>>m
Виберемо 2 атоми і позначимо амплітуди їх коливань
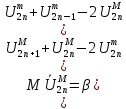
Рішення у вигляді:

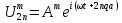
Якщо підставити рішення у систему отримаємо систему алгебраїчних рівнянь
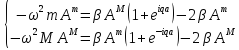
Рішення системи буде не тривіальним,коли детермінант системи=0
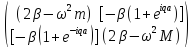
Отримаємо з-н дисперсії:
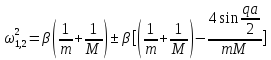
Розглянемо q=0
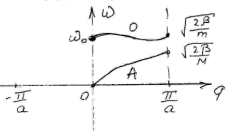
Розглянемо
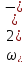
Розкладемо корінь у ряд ы обмежимося першим ы другим членами.
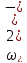
Для
малих q
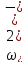 має
лінійну залежність.
має
лінійну залежність.
Нехай
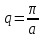 ,
,
Розглянемо випадок ∞ довгих хвиль
а)
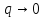
б)
нескінченно
коротких
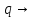
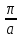

Підставимо
значення частот
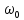 для
для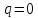 (вип.а)
у систему алгебраїчних р-нь (у сис. а) і
отримаємо для акустичної гілки(коли
ω=0).
(вип.а)
у систему алгебраїчних р-нь (у сис. а) і
отримаємо для акустичної гілки(коли
ω=0).
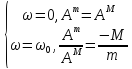

У загальному 3D випадку:
S-кількість ат. у примітивній комірці кристалу.
У
кристалі без центру симетрії пружні
оптичні хвилі створюють поляризацію
 і
ел. поле
і
ел. поле
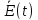 які змінюються у часі і просторі
відповідно до руху атомів.
які змінюються у часі і просторі
відповідно до руху атомів.
Коли коливання народжує поперечну хвилю поляриз.поле=0
Для повздовжніх хвиль поле ≠0
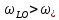
Частоти повздовжніх коливань більші за частоти поперечних.

Можуть утв збудження, які мають частково механічну, а частково електричну природу, які назив фоновими поляритонами.З’являються гібридні утворення –поляритони.